Graph The Line 2x Y 4
faraar
Sep 13, 2025 · 6 min read
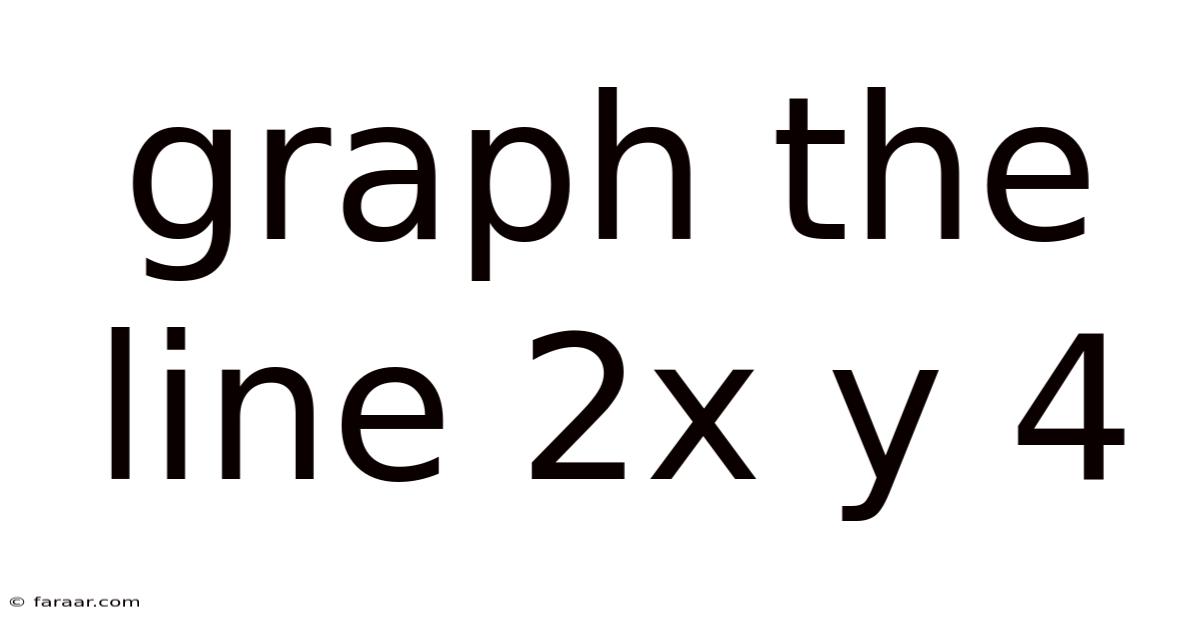
Table of Contents
Graphing the Line 2x + y = 4: A Comprehensive Guide
Understanding how to graph linear equations is a fundamental skill in algebra. This article will provide a comprehensive guide on graphing the line represented by the equation 2x + y = 4, exploring various methods and delving into the underlying mathematical concepts. We'll cover multiple approaches, including using intercepts, converting to slope-intercept form, and using a table of values, ensuring a thorough understanding for learners of all levels.
Introduction: Understanding Linear Equations
A linear equation is an equation that represents a straight line on a coordinate plane. It's typically written in the form Ax + By = C, where A, B, and C are constants, and x and y are variables. Our equation, 2x + y = 4, falls directly into this category. Graphing this equation means visually representing all the points (x, y) that satisfy this equation on a Cartesian coordinate system. This article will demonstrate several methods to achieve this effectively.
Method 1: Using the x and y-Intercepts
The x-intercept is the point where the line crosses the x-axis (where y = 0), and the y-intercept is the point where the line crosses the y-axis (where x = 0). Finding these intercepts provides two points that define the line.
-
Finding the x-intercept: Set y = 0 in the equation 2x + y = 4: 2x + 0 = 4 2x = 4 x = 2 Therefore, the x-intercept is (2, 0).
-
Finding the y-intercept: Set x = 0 in the equation 2x + y = 4: 2(0) + y = 4 y = 4 Therefore, the y-intercept is (0, 4).
Now, plot these two points (2, 0) and (0, 4) on a coordinate plane. Draw a straight line passing through these two points. This line represents the graph of the equation 2x + y = 4.
Method 2: Converting to Slope-Intercept Form (y = mx + b)
The slope-intercept form of a linear equation is y = mx + b, where 'm' represents the slope (the steepness of the line) and 'b' represents the y-intercept. Converting our equation into this form makes graphing easier.
Let's rearrange the equation 2x + y = 4 to isolate y:
y = -2x + 4
Now we can easily identify the slope and y-intercept:
- Slope (m) = -2: This means that for every 1 unit increase in x, y decreases by 2 units. The negative sign indicates a downward slope.
- y-intercept (b) = 4: This confirms our earlier finding that the line crosses the y-axis at the point (0, 4).
To graph this, start by plotting the y-intercept (0, 4). Then, use the slope to find another point. Since the slope is -2, we can move 1 unit to the right and 2 units down from the y-intercept. This gives us the point (1, 2). Plot this point and draw a straight line passing through both points (0, 4) and (1, 2). This line will be identical to the one obtained using the intercept method.
Method 3: Creating a Table of Values
This method involves creating a table of x and y values that satisfy the equation. Choose a few values for x, substitute them into the equation 2x + y = 4, and solve for the corresponding y values.
| x | y | (x, y) |
|---|---|---|
| -1 | 6 | (-1, 6) |
| 0 | 4 | (0, 4) |
| 1 | 2 | (1, 2) |
| 2 | 0 | (2, 0) |
| 3 | -2 | (3, -2) |
Plot these points (-1, 6), (0, 4), (1, 2), (2, 0), and (3, -2) on the coordinate plane. You'll observe that they all lie on the same straight line, confirming the graph of the equation 2x + y = 4.
Understanding the Slope and its Significance
The slope, m = -2, provides crucial information about the line. A negative slope indicates a line that descends from left to right. The magnitude of the slope (2 in this case) indicates the steepness; a larger magnitude means a steeper line. The slope represents the rate of change of y with respect to x. In this context, for every unit increase in x, y decreases by 2 units.
The y-Intercept and its Interpretation
The y-intercept, b = 4, represents the value of y when x is 0. Graphically, it's the point where the line intersects the y-axis. It provides a starting point for graphing the line, particularly when using the slope-intercept method.
Further Exploration: Parallel and Perpendicular Lines
Understanding the slope allows us to explore relationships between lines. Lines with the same slope are parallel, meaning they never intersect. Lines with slopes that are negative reciprocals of each other are perpendicular, meaning they intersect at a right angle. For instance, a line perpendicular to 2x + y = 4 would have a slope of 1/2.
Applications of Linear Equations
Linear equations have numerous applications across various fields:
- Physics: Describing motion, calculating velocity and acceleration.
- Economics: Modeling supply and demand, analyzing cost functions.
- Computer Science: Representing data relationships, developing algorithms.
- Engineering: Designing structures, analyzing circuits.
Frequently Asked Questions (FAQ)
Q1: Can I graph this equation using only one point?
A1: No, you need at least two points to define a straight line. While one point can be on a line, infinitely many lines can pass through a single point.
Q2: What if the equation is not in the standard form (Ax + By = C)?
A2: You can manipulate the equation algebraically to bring it into the standard form or the slope-intercept form (y = mx + b) before graphing.
Q3: What if the slope is undefined?
A3: An undefined slope indicates a vertical line. The equation of a vertical line is of the form x = k, where k is a constant.
Q4: What if the slope is zero?
A4: A zero slope indicates a horizontal line. The equation of a horizontal line is of the form y = k, where k is a constant.
Q5: How can I check if my graph is accurate?
A5: Substitute the coordinates of any point on your drawn line back into the original equation (2x + y = 4). If the equation holds true, your graph is accurate. You can also check if the slope and y-intercept match your calculations.
Conclusion: Mastering Linear Equation Graphing
Graphing linear equations, such as 2x + y = 4, is a fundamental skill in mathematics with broad applications. This guide has explored three effective methods: using intercepts, converting to slope-intercept form, and using a table of values. Understanding the concepts of slope and y-intercept is crucial for interpreting the graph and its implications. Mastering these techniques will empower you to tackle more complex mathematical problems and build a strong foundation in algebra and related fields. Remember to practice regularly to solidify your understanding and build confidence in graphing linear equations.
Latest Posts
Latest Posts
-
Complete The Balanced Molecular Chemical Equation For The Reaction Below
Sep 13, 2025
-
How Much Is Half A Pound Of Cheese
Sep 13, 2025
-
Violin Classes Near Me For Beginners
Sep 13, 2025
-
How To Find Percentile On Ti 84
Sep 13, 2025
-
Compute Displaystyle Left Frac 8 125 Right 1 3
Sep 13, 2025
Related Post
Thank you for visiting our website which covers about Graph The Line 2x Y 4 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.