2 3 Divided By 1 3 As A Fraction
faraar
Sep 13, 2025 · 6 min read
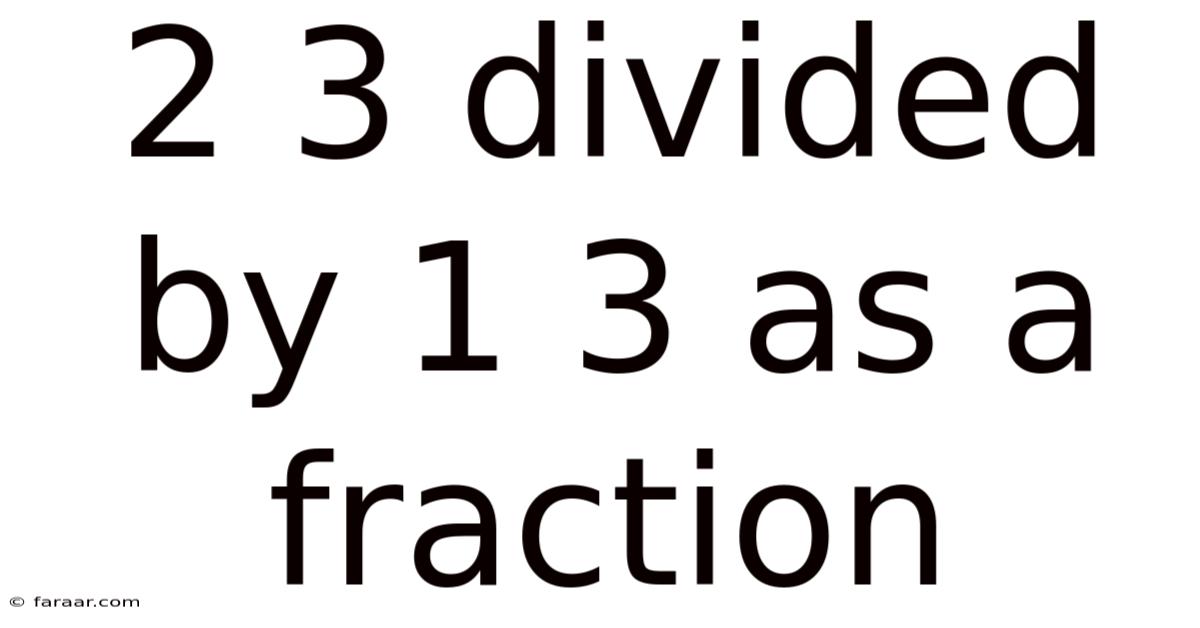
Table of Contents
Understanding 2/3 Divided by 1/3: A Comprehensive Guide
Dividing fractions can seem daunting at first, but with a clear understanding of the underlying principles, it becomes a straightforward process. This article will guide you through the steps of dividing 2/3 by 1/3, explaining the process in detail, exploring the underlying mathematical concepts, and addressing frequently asked questions. We'll move beyond simply finding the answer to build a strong foundational understanding of fraction division.
Introduction: Why Learn Fraction Division?
Fractions are fundamental to mathematics and appear in various real-world applications, from cooking and construction to finance and science. Mastering fraction division is crucial for tackling more complex mathematical problems and successfully applying mathematical concepts to practical situations. This seemingly simple problem, 2/3 divided by 1/3, serves as an excellent stepping stone to understanding broader principles of fraction manipulation.
Understanding the Concept of Division
Before diving into the specifics of dividing fractions, let's refresh our understanding of division itself. Division essentially asks the question: "How many times does one number fit into another?" For example, 6 ÷ 2 asks, "How many times does 2 fit into 6?" The answer, of course, is 3. This same principle applies to fractions, although the process might seem a little more abstract initially.
Method 1: The "Keep, Change, Flip" Method
This is perhaps the most common and easily remembered method for dividing fractions. It's a shortcut that simplifies the process significantly. The steps are as follows:
- Keep: Keep the first fraction exactly as it is. In our case, this remains 2/3.
- Change: Change the division sign (÷) to a multiplication sign (×).
- Flip: Flip (or find the reciprocal of) the second fraction. The reciprocal of 1/3 is 3/1 (or simply 3).
Therefore, the problem 2/3 ÷ 1/3 becomes:
2/3 × 3/1
Now, we simply multiply the numerators (top numbers) together and the denominators (bottom numbers) together:
(2 × 3) / (3 × 1) = 6/3
Finally, we simplify the resulting fraction:
6/3 = 2
Therefore, 2/3 divided by 1/3 equals 2.
Method 2: Using the Reciprocal and Multiplication
This method explains the why behind the "Keep, Change, Flip" method. Division by a fraction is equivalent to multiplication by its reciprocal. The reciprocal of a fraction is obtained by swapping the numerator and the denominator. For instance, the reciprocal of 1/3 is 3/1.
So, 2/3 ÷ 1/3 can be rewritten as:
2/3 × 3/1
Again, multiplying the numerators and denominators gives us:
(2 × 3) / (3 × 1) = 6/3 = 2
This method underscores the mathematical reasoning behind the shortcut, solidifying your understanding of why the "Keep, Change, Flip" method works.
Method 3: Visual Representation
While the above methods are efficient, visualizing the problem can enhance comprehension. Imagine you have 2/3 of a pizza. You want to divide this 2/3 into portions that are each 1/3 of the pizza. How many 1/3 portions do you have?
If you divide your 2/3 pizza into pieces that are each 1/3 of a whole pizza, you will have exactly two pieces. This visual representation reinforces the answer we obtained using the other methods.
Explanation with Different Fractions: Extending the Concept
Let's try another example to further solidify your understanding. Consider the problem 4/5 ÷ 2/5.
Using the "Keep, Change, Flip" method:
- Keep: 4/5
- Change: ÷ becomes ×
- Flip: 2/5 becomes 5/2
This gives us:
4/5 × 5/2 = (4 × 5) / (5 × 2) = 20/10 = 2
Again, the answer is 2. This demonstrates that the method works consistently across different fractions.
Let’s try a slightly more challenging example: 1/2 ÷ 1/4
Following the same method:
- Keep: 1/2
- Change: ÷ becomes ×
- Flip: 1/4 becomes 4/1
This results in:
1/2 × 4/1 = (1 × 4) / (2 × 1) = 4/2 = 2
Notice that in this example, we are dividing a smaller fraction (1/2) by an even smaller fraction (1/4). The result is greater than 1, illustrating that dividing by a fraction smaller than 1 results in a larger number.
Dealing with Mixed Numbers
Mixed numbers (e.g., 1 1/2) require an extra step before applying the fraction division methods. You must first convert the mixed number into an improper fraction. An improper fraction has a numerator larger than or equal to its denominator.
Let's say we need to solve 1 1/2 ÷ 1/3.
First, convert 1 1/2 into an improper fraction:
1 1/2 = (1 × 2 + 1) / 2 = 3/2
Now, we can apply the "Keep, Change, Flip" method:
- Keep: 3/2
- Change: ÷ becomes ×
- Flip: 1/3 becomes 3/1
This becomes:
3/2 × 3/1 = (3 × 3) / (2 × 1) = 9/2 = 4 1/2
Therefore, 1 1/2 ÷ 1/3 = 4 1/2
Mathematical Explanation: Why Does "Keep, Change, Flip" Work?
The "Keep, Change, Flip" method is a shortcut, but its underlying principle rests on the definition of division and the properties of reciprocals. Dividing by a number is the same as multiplying by its multiplicative inverse (reciprocal).
Consider the general case: a/b ÷ c/d
This can be written as:
(a/b) × (d/c)
This is equivalent to:
(a × d) / (b × c)
This is precisely what the "Keep, Change, Flip" method accomplishes in a simpler, more intuitive way.
Frequently Asked Questions (FAQ)
- Q: What if I have a whole number in the division problem?
A: Treat the whole number as a fraction with a denominator of 1. For example, 4 ÷ 1/2 becomes 4/1 ÷ 1/2. Then, apply the "Keep, Change, Flip" method.
- Q: Can I use a calculator to divide fractions?
A: Yes, most calculators have fraction functionalities that allow you to input fractions directly and obtain the answer. However, understanding the manual methods is crucial for building a strong foundation in mathematics and for solving problems where a calculator may not be readily available.
- Q: What if the result is an improper fraction?
A: It's perfectly acceptable to leave the result as an improper fraction. However, you can also convert it to a mixed number for easier interpretation in certain contexts.
- Q: Are there other methods to divide fractions?
A: While the "Keep, Change, Flip" method is the most efficient and commonly used, you can also find a common denominator and then divide the numerators. This method, however, is generally more time-consuming.
Conclusion: Mastering Fraction Division
Dividing fractions might seem challenging initially, but by understanding the underlying principles and employing the "Keep, Change, Flip" method or the reciprocal method, it becomes a manageable and even straightforward process. Remember to practice regularly with various examples, including mixed numbers and whole numbers, to solidify your understanding and build confidence in your ability to tackle fraction division problems effectively. The ability to confidently work with fractions is a valuable skill that will serve you well throughout your mathematical journey. Don't be afraid to visualize the problems; drawing diagrams can often illuminate the underlying concepts more clearly. With consistent practice and a clear understanding of the concepts, mastering fraction division will become second nature.
Latest Posts
Latest Posts
-
What Happens To The Medium When A Wave Moves
Sep 13, 2025
-
How Many Cups In 5 Gallons Of Water
Sep 13, 2025
-
Find The Height Of A Rectangular Prism
Sep 13, 2025
-
450 Miles Is How Many Hours
Sep 13, 2025
-
Find The Perimeter Of Equilateral Triangle
Sep 13, 2025
Related Post
Thank you for visiting our website which covers about 2 3 Divided By 1 3 As A Fraction . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.