1/2 Divided By 3/4 In A Fraction
faraar
Sep 22, 2025 · 5 min read
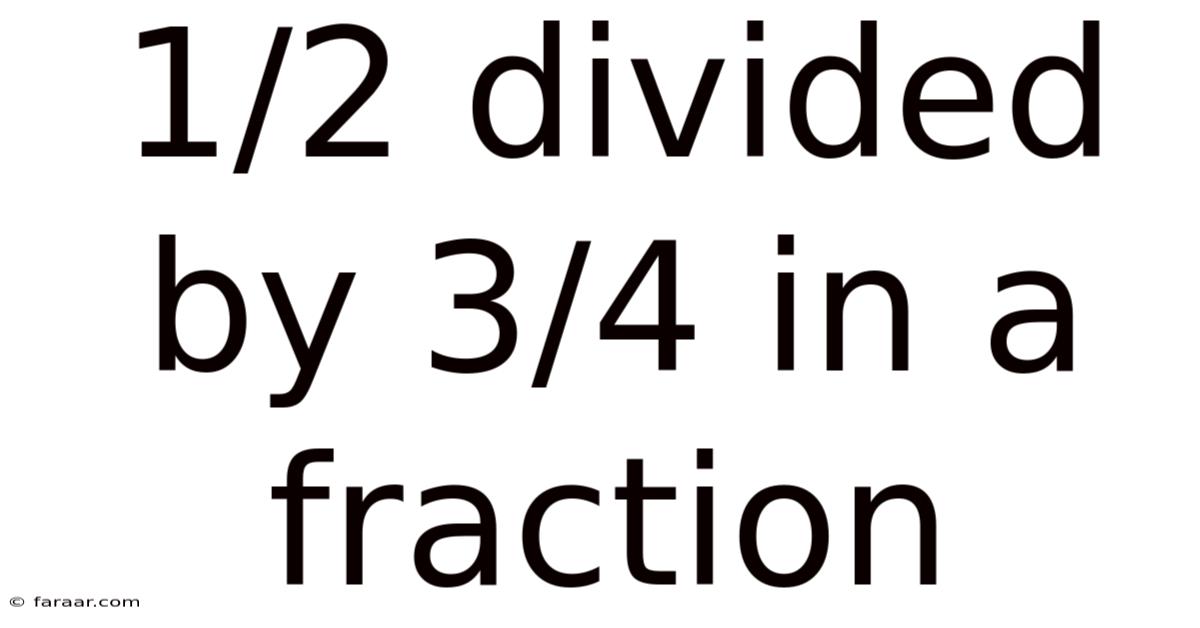
Table of Contents
Dividing Fractions: A Deep Dive into 1/2 Divided by 3/4
Understanding how to divide fractions is a fundamental skill in mathematics, crucial for various applications from baking to advanced calculus. This comprehensive guide will explore the division of fractions, using the example of 1/2 divided by 3/4, and delve into the underlying principles to build a strong conceptual understanding. We'll break down the process step-by-step, explain the underlying rationale, and answer frequently asked questions. By the end, you'll not only know how to solve this specific problem but also possess the confidence to tackle any fraction division challenge.
Understanding Fraction Division: The "Invert and Multiply" Method
The most common method for dividing fractions is the "invert and multiply" method. This seemingly simple technique hides a deeper mathematical truth, which we'll explore later. For now, let's apply it to our problem: 1/2 ÷ 3/4.
Step 1: Invert the second fraction (the divisor).
This means flipping the numerator and denominator. So, 3/4 becomes 4/3.
Step 2: Change the division sign to a multiplication sign.
Our problem now transforms from 1/2 ÷ 3/4 to 1/2 x 4/3.
Step 3: Multiply the numerators together and the denominators together.
Numerator: 1 x 4 = 4 Denominator: 2 x 3 = 6
Step 4: Simplify the resulting fraction (if possible).
We have 4/6. Both 4 and 6 are divisible by 2, so we simplify to 2/3.
Therefore, 1/2 ÷ 3/4 = 2/3.
A Visual Representation: Understanding the "Why"
While the "invert and multiply" method provides a quick solution, it's crucial to grasp the underlying logic. Let's visualize this division using a simple example.
Imagine you have 1/2 of a pizza. You want to divide this half-pizza into portions that are each 3/4 the size of a whole pizza. How many such portions can you get?
This is exactly what 1/2 ÷ 3/4 represents. To solve this visually, we could represent 1/2 as a rectangle divided in half, then overlay a grid representing 3/4 of a whole. You'll find that 2/3 of the grid perfectly fits within the 1/2 rectangle.
The Mathematical Rationale Behind "Invert and Multiply"
The "invert and multiply" rule isn't a magical trick; it's derived from the fundamental properties of fractions and reciprocals.
Remember that dividing by a number is the same as multiplying by its reciprocal. The reciprocal of a fraction is simply the fraction flipped upside down. For example, the reciprocal of 3/4 is 4/3.
So, when we divide 1/2 by 3/4, we're essentially multiplying 1/2 by the reciprocal of 3/4, which is 4/3. This is precisely what the "invert and multiply" method does.
Dealing with Mixed Numbers
What if your division problem involves mixed numbers (like 1 1/2 ÷ 2 1/4)? The first step is to convert the mixed numbers into improper fractions.
- Converting Mixed Numbers to Improper Fractions: To convert a mixed number to an improper fraction, multiply the whole number by the denominator, add the numerator, and keep the same denominator.
For example:
- 1 1/2 = (1 x 2 + 1) / 2 = 3/2
- 2 1/4 = (2 x 4 + 1) / 4 = 9/4
Now, the problem becomes 3/2 ÷ 9/4. Follow the "invert and multiply" method:
- Invert the second fraction: 9/4 becomes 4/9
- Change the division to multiplication: 3/2 x 4/9
- Multiply numerators and denominators: (3 x 4) / (2 x 9) = 12/18
- Simplify: 12/18 simplifies to 2/3
Therefore, 1 1/2 ÷ 2 1/4 = 2/3
Dividing Fractions with Whole Numbers
Dividing a fraction by a whole number or vice versa is a special case of fraction division. Remember that any whole number can be expressed as a fraction with a denominator of 1.
For example, to divide 1/2 by 3, we rewrite 3 as 3/1:
1/2 ÷ 3/1 = 1/2 x 1/3 = 1/6
And to divide 3 by 1/2:
3/1 ÷ 1/2 = 3/1 x 2/1 = 6/1 = 6
Complex Fraction Division
Sometimes, you might encounter more complex scenarios involving fractions within fractions (complex fractions). The key is to simplify the numerator and denominator separately before applying the "invert and multiply" rule.
Frequently Asked Questions (FAQ)
Q: Why does the "invert and multiply" method work?
A: The method is based on the concept of reciprocals. Dividing by a number is equivalent to multiplying by its reciprocal. Inverting the second fraction and multiplying is a shortcut to performing this multiplication.
Q: What if I get a large fraction after multiplying?
A: Always simplify the resulting fraction to its lowest terms by finding the greatest common divisor (GCD) of the numerator and denominator and dividing both by it.
Q: Can I use a calculator to divide fractions?
A: Most calculators can handle fraction division. However, understanding the underlying principles is crucial for solving more complex problems and developing mathematical intuition.
Q: Is there another way to divide fractions besides "invert and multiply"?
A: While less common, you could find a common denominator for both fractions and then divide the numerators. However, the "invert and multiply" method is generally more efficient and straightforward.
Conclusion: Mastering Fraction Division
Dividing fractions, while initially seeming daunting, becomes manageable with a solid understanding of the "invert and multiply" method and its underlying mathematical reasoning. This article has provided a detailed explanation, visual aids, and addressed frequently asked questions to solidify your understanding. Remember to practice regularly, and soon you'll confidently tackle any fraction division problem that comes your way. The ability to divide fractions is a building block for more advanced mathematical concepts and holds practical applications in numerous fields. With consistent practice and a thorough grasp of the principles outlined here, you'll be well-equipped to handle fractions with ease and confidence. Continue practicing different types of fraction division problems, and don't hesitate to revisit this guide if you need a refresher. Mastering this fundamental skill will significantly enhance your mathematical proficiency and open doors to further exploration of mathematical concepts.
Latest Posts
Latest Posts
-
Find All The Real Fourth Roots Of 256
Sep 22, 2025
-
1 4 Divided By 1 3 In Fraction
Sep 22, 2025
-
Scores On The Sat Exam Follows The Distribution
Sep 22, 2025
-
Greatest Common Factor Of 56 And 32
Sep 22, 2025
-
Is 1 2 Greater Than 2 4
Sep 22, 2025
Related Post
Thank you for visiting our website which covers about 1/2 Divided By 3/4 In A Fraction . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.