Is 1 2 Greater Than 2 4
faraar
Sep 22, 2025 · 6 min read
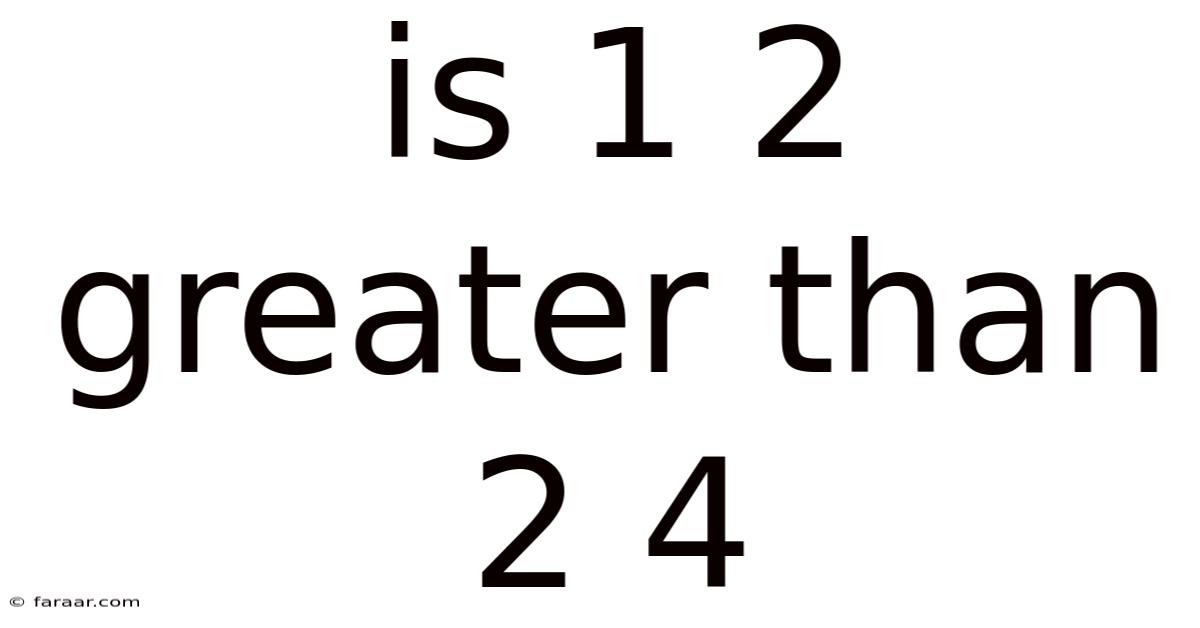
Table of Contents
Is 1/2 Greater Than 2/4? A Deep Dive into Fractions and Equivalence
This article explores the seemingly simple question: Is 1/2 greater than 2/4? While the answer might seem obvious to some, a thorough understanding of fractions, their representation, and the concept of equivalence is crucial for a solid grasp of mathematical foundations. We'll delve into the core principles, explore different methods for comparing fractions, and address common misconceptions. This comprehensive guide will leave you with a confident understanding of how to compare fractions of all types.
Understanding Fractions: Parts of a Whole
Before we tackle the comparison, let's refresh our understanding of fractions. A fraction represents a part of a whole. It's composed of two key components:
- Numerator: The top number, indicating how many parts we have.
- Denominator: The bottom number, indicating how many equal parts the whole is divided into.
For example, in the fraction 1/2, the numerator (1) tells us we have one part, and the denominator (2) tells us the whole is divided into two equal parts. This means we have one-half of the whole.
Similarly, 2/4 means we have two parts out of a whole divided into four equal parts. This is often visualized as two slices of a pizza cut into four equal slices.
Visualizing the Comparison: The Power of Representation
One of the easiest ways to compare 1/2 and 2/4 is through visualization. Imagine two identical circles:
- Circle 1: Divide this circle into two equal halves and shade one half. This represents 1/2.
- Circle 2: Divide this circle into four equal quarters and shade two of them. This represents 2/4.
By visually comparing the shaded areas of both circles, it becomes immediately clear that the shaded portions are identical in size. This visual representation powerfully demonstrates that 1/2 and 2/4 are equivalent fractions.
Equivalent Fractions: The Same Value, Different Representation
Equivalent fractions represent the same proportion or value, even though they look different. They are like different ways of expressing the same amount. We can obtain equivalent fractions by multiplying or dividing both the numerator and the denominator by the same non-zero number.
In our case:
- If we multiply both the numerator and denominator of 1/2 by 2, we get (1 x 2) / (2 x 2) = 2/4.
- Conversely, if we divide both the numerator and denominator of 2/4 by 2, we get (2 ÷ 2) / (4 ÷ 2) = 1/2.
This clearly shows that 1/2 and 2/4 are equivalent fractions; they represent the same quantity. Therefore, 1/2 is not greater than 2/4; they are equal.
Comparing Fractions: Methods and Techniques
While visualization is helpful, especially for simpler fractions, other methods are necessary for comparing more complex fractions. Here are some common techniques:
-
Finding a Common Denominator: This is a fundamental method. To compare fractions, convert them to equivalent fractions with the same denominator. Then, compare the numerators. The fraction with the larger numerator is the larger fraction.
For instance, to compare 1/3 and 2/5, we find the least common multiple (LCM) of 3 and 5, which is 15. Then:
- 1/3 = (1 x 5) / (3 x 5) = 5/15
- 2/5 = (2 x 3) / (5 x 3) = 6/15
Since 6/15 > 5/15, we conclude that 2/5 > 1/3.
-
Converting to Decimals: Another approach is to convert the fractions to decimals by dividing the numerator by the denominator. Then, compare the decimal values.
- 1/2 = 0.5
- 2/4 = 0.5
Again, this confirms that 1/2 and 2/4 are equal.
-
Cross-Multiplication: For comparing two fractions, a/b and c/d, cross-multiply:
- If a x d > b x c, then a/b > c/d
- If a x d < b x c, then a/b < c/d
- If a x d = b x c, then a/b = c/d
Let's use this to compare 3/5 and 2/3:
- 3 x 3 = 9
- 5 x 2 = 10
Since 9 < 10, we have 3/5 < 2/3.
Simplifying Fractions: Reducing to Lowest Terms
Simplifying fractions involves reducing them to their lowest terms by dividing both the numerator and the denominator by their greatest common divisor (GCD). This makes comparing fractions easier and helps in understanding their value more clearly.
For example, 2/4 can be simplified by dividing both the numerator and the denominator by their GCD, which is 2. This gives us 1/2. Simplifying fractions doesn't change their value, only their representation.
Addressing Common Misconceptions
A common misconception is that the larger the numbers in a fraction, the larger the fraction itself. This is incorrect. The relative size of the numerator and denominator matters more than their absolute values. For example, 1/2 is larger than 1/10, even though the numbers in 1/10 are larger than those in 1/2.
Another misconception is confusing addition and comparison. Remember, we are not adding the fractions but comparing their sizes.
Conclusion: Equivalence and Understanding
The question, "Is 1/2 greater than 2/4?" highlights the importance of understanding equivalent fractions. We have definitively shown that 1/2 is not greater than 2/4; they are equal. Mastering the techniques for comparing fractions, including finding common denominators, converting to decimals, cross-multiplication, and simplifying fractions, is essential for building a strong mathematical foundation. By understanding these concepts, you can confidently tackle more complex fraction problems and comparisons. This knowledge isn't just limited to math class; it’s a fundamental skill applicable in numerous real-world scenarios, from baking to construction to financial calculations. So, take the time to truly understand these concepts and you'll unlock a powerful tool for problem-solving.
Frequently Asked Questions (FAQ)
Q1: Can all fractions be expressed as equivalent fractions?
A1: Yes, infinitely many equivalent fractions can be created for any given fraction by multiplying or dividing the numerator and denominator by the same non-zero number.
Q2: What is the best method for comparing fractions?
A2: There isn't one "best" method. The most efficient approach depends on the specific fractions being compared. Finding a common denominator is generally reliable, while converting to decimals is often easier for quick comparisons. Cross-multiplication is a powerful method for directly comparing two fractions.
Q3: How can I improve my understanding of fractions?
A3: Practice is key! Work through various examples, use visual aids, and try different comparison methods to build your confidence and understanding. Focus on understanding the underlying concepts rather than just memorizing procedures. Utilize online resources, practice problems, and educational videos for a comprehensive understanding.
Q4: Are there any resources available to help me learn more about fractions?
A4: Numerous online resources, educational websites, and textbooks cover the topic of fractions in detail. These resources often include interactive exercises and tutorials that cater to different learning styles.
Q5: What is the significance of simplifying fractions?
A5: Simplifying fractions makes them easier to understand and compare. Working with fractions in their simplest form minimizes computational errors and improves the overall efficiency of solving problems involving fractions. It also makes identifying equivalent fractions simpler.
Latest Posts
Latest Posts
-
How To Say Know In Italian
Sep 22, 2025
-
How To Determine Whether The Function Is A Polynomial Function
Sep 22, 2025
-
How To Graph X 2y 6
Sep 22, 2025
-
The Hardest Math Question With Answer
Sep 22, 2025
-
How Do You Find The Sum Of Interior Angles
Sep 22, 2025
Related Post
Thank you for visiting our website which covers about Is 1 2 Greater Than 2 4 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.