Find All The Real Fourth Roots Of 256
faraar
Sep 22, 2025 · 7 min read
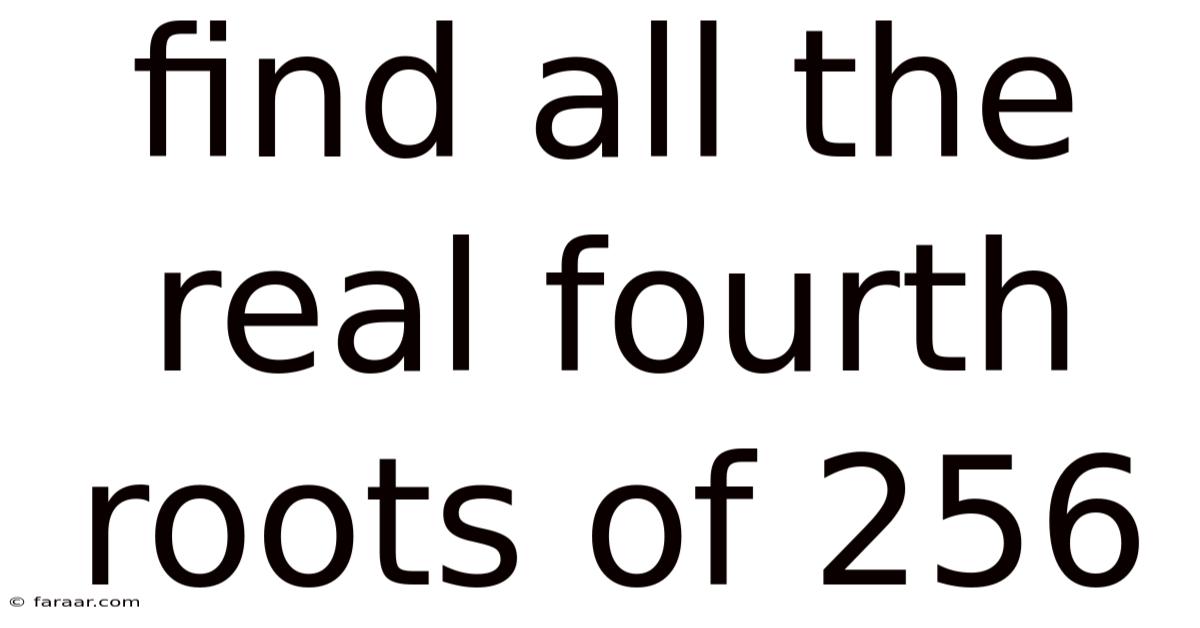
Table of Contents
Finding All the Real Fourth Roots of 256: A Comprehensive Guide
Finding the fourth roots of a number, especially a seemingly simple one like 256, might appear straightforward at first glance. However, understanding the concept fully requires delving into the complexities of complex numbers and their representation in the complex plane. This article will provide a detailed exploration of how to find all the fourth roots of 256, explaining the process step-by-step and clarifying the mathematical concepts involved. We'll cover both the real and complex roots, ensuring a comprehensive understanding of this fundamental mathematical operation.
Introduction: Understanding Roots and the Fundamental Theorem of Algebra
Before diving into the specifics of finding the fourth roots of 256, let's establish a foundational understanding. The nth root of a number x is a number r such that r<sup>n</sup> = x. For example, the square root of 9 (√9) is 3 because 3² = 9. However, we must remember that negative numbers also have square roots; (-3)² is also 9. This introduces the concept of multiple roots.
The Fundamental Theorem of Algebra states that a polynomial of degree n has exactly n roots, counting multiplicities, in the complex number system. This means a polynomial equation of the form x<sup>n</sup> - a = 0 will have n distinct solutions (roots) which can be real or complex numbers. In our case, we are dealing with the equation x<sup>4</sup> - 256 = 0, a polynomial of degree 4, indicating that there are four fourth roots of 256.
Finding the Real Fourth Roots of 256
Let's start by finding the real fourth roots. This is the simplest approach and is often the first step in tackling such problems. We are looking for real numbers r such that r<sup>4</sup> = 256.
We can begin by considering positive real numbers:
- Positive root: We know that 4 x 4 x 4 x 4 = 256, so 4 is one of the fourth roots of 256.
Now, let's consider negative real numbers:
- Negative root: It's crucial to remember that raising a negative number to an even power results in a positive number. Therefore, (-4)<sup>4</sup> = ((-4)²)² = 16² = 256. Thus, -4 is also a fourth root of 256.
Therefore, we've identified two real fourth roots of 256: 4 and -4.
Delving into the Complex Roots: Polar Form and De Moivre's Theorem
To find the remaining two roots, we need to venture into the realm of complex numbers. Complex numbers are numbers of the form a + bi, where a and b are real numbers, and i is the imaginary unit (√-1). Representing these numbers in polar form makes finding their roots significantly easier.
The polar form of a complex number z is given by: z = r(cos θ + i sin θ), where r is the modulus (distance from the origin in the complex plane) and θ is the argument (angle from the positive real axis).
De Moivre's Theorem provides a powerful tool for calculating the nth roots of a complex number in polar form. The theorem states that if z = r(cos θ + i sin θ), then the nth roots of z are given by:
z<sub>k</sub> = <sup>n</sup>√r [cos((θ + 2πk)/n) + i sin((θ + 2πk)/n)], where k = 0, 1, 2, ..., n-1.
Let's apply this to find the fourth roots of 256. First, we need to express 256 in polar form. Since 256 is a real number, its polar form is simply:
256 = 256(cos 0 + i sin 0) (θ = 0 because it lies on the positive real axis).
Now, using De Moivre's Theorem with n = 4 and r = 256, we calculate the four roots:
- k = 0: z<sub>0</sub> = <sup>4</sup>√256 [cos(0/4) + i sin(0/4)] = 4(cos 0 + i sin 0) = 4
- k = 1: z<sub>1</sub> = <sup>4</sup>√256 [cos((0 + 2π)/4) + i sin((0 + 2π)/4)] = 4(cos(π/2) + i sin(π/2)) = 4i
- k = 2: z<sub>2</sub> = <sup>4</sup>√256 [cos((0 + 4π)/4) + i sin((0 + 4π)/4)] = 4(cos π + i sin π) = -4
- k = 3: z<sub>3</sub> = <sup>4</sup>√256 [cos((0 + 6π)/4) + i sin((0 + 6π)/4)] = 4(cos(3π/2) + i sin(3π/2)) = -4i
Complete Set of Fourth Roots of 256
Therefore, the complete set of fourth roots of 256 are: 4, -4, 4i, and -4i. We've successfully found all four roots, as predicted by the Fundamental Theorem of Algebra. Two are real numbers, and two are purely imaginary numbers.
Graphical Representation in the Complex Plane
It's insightful to visualize these roots in the complex plane. They are evenly spaced around a circle with a radius of 4, centered at the origin. This is a general characteristic of the roots of a complex number; they form a regular polygon in the complex plane.
- 4: Lies on the positive real axis.
- 4i: Lies on the positive imaginary axis.
- -4: Lies on the negative real axis.
- -4i: Lies on the negative imaginary axis.
Explanation of the Mathematical Concepts
Let's revisit and expand on the key mathematical concepts used:
-
Complex Numbers: Numbers of the form a + bi, where a and b are real numbers, and i is the imaginary unit (√-1). They extend the real number system to encompass numbers with both real and imaginary components.
-
Polar Form: A way to represent complex numbers using their modulus (distance from the origin) and argument (angle from the positive real axis). This simplifies calculations, especially when dealing with roots and powers.
-
De Moivre's Theorem: A powerful tool for calculating the nth powers and roots of complex numbers in polar form. It significantly simplifies the process compared to algebraic manipulation of complex numbers in rectangular form.
-
Fundamental Theorem of Algebra: This fundamental theorem guarantees the existence of n roots for a polynomial of degree n. It underlines the completeness of the complex number system in solving polynomial equations.
Frequently Asked Questions (FAQ)
Q1: Why are there four roots, and not just one or two?
A1: The Fundamental Theorem of Algebra dictates that a polynomial of degree n has exactly n roots (counting multiplicities). Since x<sup>4</sup> - 256 = 0 is a polynomial of degree 4, it has four roots.
Q2: Are all fourth roots of numbers always complex numbers?
A2: No. If the number is positive, there will always be at least one positive real root. For even-powered roots of positive real numbers, there will always be both a positive and a negative real root. Complex roots only emerge when we consider numbers with negative values or complex numbers as the base.
Q3: How can I verify my solutions?
A3: Simply raise each of the four roots (4, -4, 4i, -4i) to the power of 4. You should obtain 256 in each case, confirming that they are indeed fourth roots.
Conclusion: Mastering the Fourth Roots of 256 and Beyond
Finding all the fourth roots of 256 involves a journey from simple arithmetic to the fascinating world of complex numbers. By understanding the Fundamental Theorem of Algebra, polar form representation, and De Moivre's Theorem, we are equipped to tackle similar problems effectively. The process not only provides the solutions (4, -4, 4i, -4i) but also reinforces a deeper appreciation for the richness and complexity of the number system. This detailed explanation should empower you to approach such problems confidently and expand your mathematical understanding beyond the seemingly simple realm of real numbers. Remember to practice with different numbers and powers to solidify your grasp of these concepts. The more you engage with these ideas, the more intuitive and straightforward they will become.
Latest Posts
Latest Posts
-
A Doctor Wants To Estimate The Mean Hdl
Sep 22, 2025
-
Which Shows How To Determine The Volume Of The Pyramid
Sep 22, 2025
-
How To Say Know In Italian
Sep 22, 2025
-
How To Determine Whether The Function Is A Polynomial Function
Sep 22, 2025
-
How To Graph X 2y 6
Sep 22, 2025
Related Post
Thank you for visiting our website which covers about Find All The Real Fourth Roots Of 256 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.