What Is Greater 1 2 Or 2 3
faraar
Sep 09, 2025 · 5 min read
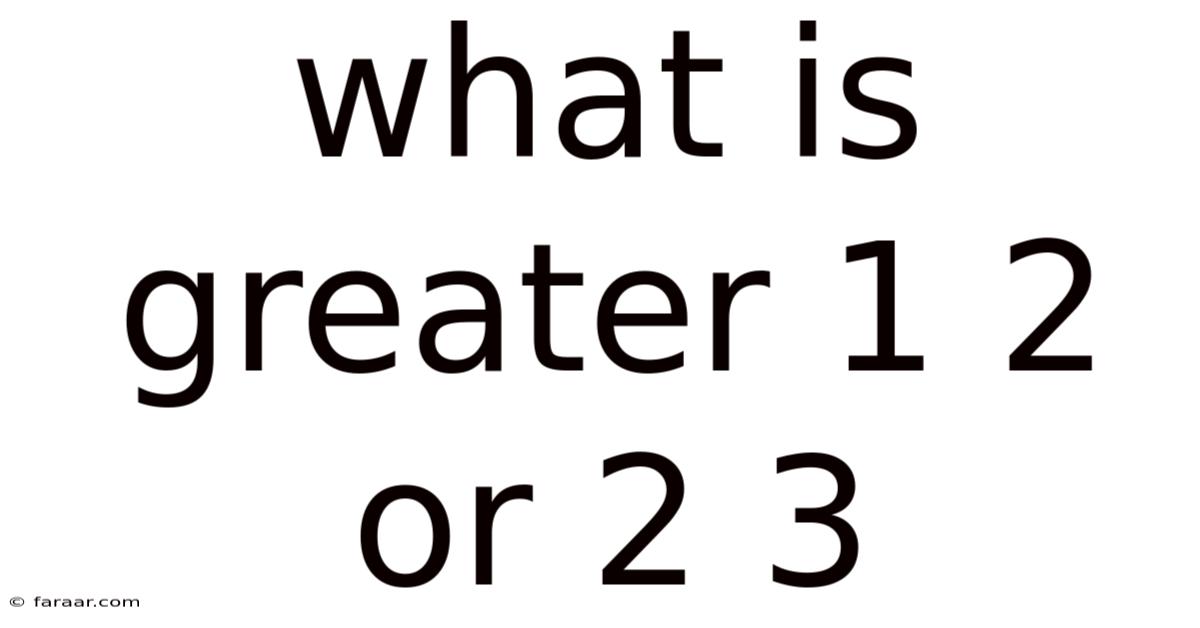
Table of Contents
What's Greater: 1/2 or 2/3? A Deep Dive into Fraction Comparison
Understanding fractions is fundamental to mathematics, and comparing fractions is a skill crucial for many areas, from basic arithmetic to advanced calculus. This seemingly simple question – "What's greater: 1/2 or 2/3?" – provides a fantastic opportunity to explore several methods for comparing fractions and understand the underlying principles. This article will not only answer the question definitively but will also equip you with the tools to compare any two fractions confidently.
Understanding Fractions
Before diving into comparison, let's refresh our understanding of fractions. A fraction represents a part of a whole. It's written as a/b, where 'a' is the numerator (the number of parts we have) and 'b' is the denominator (the total number of equal parts the whole is divided into).
For example, in the fraction 1/2, the numerator (1) represents one part, and the denominator (2) indicates that the whole is divided into two equal parts. Similarly, in 2/3, we have two parts out of a total of three equal parts.
Method 1: Finding a Common Denominator
This is perhaps the most straightforward method for comparing fractions. The key idea is to rewrite both fractions with the same denominator. This allows for a direct comparison of the numerators. To find a common denominator, we need to find the least common multiple (LCM) of the denominators.
Let's apply this to our problem: comparing 1/2 and 2/3.
-
Step 1: Find the LCM of the denominators (2 and 3). The LCM of 2 and 3 is 6.
-
Step 2: Rewrite each fraction with the common denominator (6).
-
To change 1/2 to have a denominator of 6, we multiply both the numerator and the denominator by 3: (1 x 3) / (2 x 3) = 3/6
-
To change 2/3 to have a denominator of 6, we multiply both the numerator and the denominator by 2: (2 x 2) / (3 x 2) = 4/6
-
-
Step 3: Compare the numerators. Now we have 3/6 and 4/6. Since 4 > 3, we conclude that 4/6 > 3/6, therefore 2/3 > 1/2.
Method 2: Converting to Decimals
Another effective method is to convert the fractions into decimals and then compare them. This method is particularly useful when dealing with fractions that are difficult to visualize or find a common denominator for.
To convert a fraction to a decimal, we simply divide the numerator by the denominator.
-
Step 1: Convert 1/2 to a decimal. 1 ÷ 2 = 0.5
-
Step 2: Convert 2/3 to a decimal. 2 ÷ 3 = 0.666... (a recurring decimal)
-
Step 3: Compare the decimals. Since 0.666... > 0.5, we can conclude that 2/3 > 1/2.
Method 3: Visual Representation
For those who prefer a more intuitive approach, visualizing the fractions can be helpful. Imagine two identical pies.
-
1/2: Cut one pie into two equal halves. 1/2 represents one of those halves.
-
2/3: Cut the other pie into three equal thirds. 2/3 represents two of those thirds.
By visually comparing the portions, it becomes apparent that 2/3 represents a larger portion than 1/2. This method is especially useful for understanding the concept of fraction comparison, particularly for beginners.
Method 4: Cross-Multiplication
This method provides a quick way to compare fractions without finding a common denominator. It relies on the principle that if a/b > c/d, then a x d > b x c.
-
Step 1: Cross-multiply the numerators and denominators.
-
Multiply the numerator of the first fraction (1) by the denominator of the second fraction (3): 1 x 3 = 3
-
Multiply the numerator of the second fraction (2) by the denominator of the first fraction (2): 2 x 2 = 4
-
-
Step 2: Compare the results. Since 4 > 3, we conclude that 2/3 > 1/2.
The Importance of Understanding Fraction Comparison
The ability to compare fractions is a fundamental skill that extends beyond simple arithmetic problems. It's crucial for:
-
Solving word problems: Many real-world scenarios involve fractions, such as calculating proportions, sharing resources, or understanding measurements.
-
Algebra and Calculus: Fraction comparison is a building block for more advanced mathematical concepts.
-
Data analysis: Interpreting data often involves comparing fractions or ratios.
-
Everyday life: From cooking (measuring ingredients) to budgeting (understanding percentages), comparing fractions is a valuable life skill.
Frequently Asked Questions (FAQ)
Q: Can I always use the common denominator method?
A: Yes, the common denominator method always works, although it can be less efficient than cross-multiplication for larger numbers.
Q: What if the fractions are negative?
A: The methods described above still apply, but remember that negative fractions work in reverse order. For example, -1/2 > -2/3 because -1/2 is closer to 0.
Q: Are there other methods to compare fractions?
A: While the methods mentioned above are the most common and efficient, there are other less frequently used techniques, often involving converting fractions to percentages or using number lines.
Q: Why is it important to learn multiple methods?
A: Learning multiple methods provides flexibility and allows you to choose the most efficient approach depending on the specific fractions being compared. It also enhances your understanding of the underlying mathematical principles.
Conclusion
The answer to the question, "What's greater: 1/2 or 2/3?" is definitively 2/3. This article has explored four different methods for comparing fractions, highlighting their strengths and applications. Mastering these methods will empower you to confidently compare any two fractions, a skill essential for success in mathematics and beyond. Remember, understanding fractions isn't just about memorizing rules; it's about developing a deep understanding of their meaning and representation. Through visualization, practice, and understanding the underlying principles, you can become proficient in comparing fractions and apply this skill to various real-world scenarios. So, the next time you encounter a fraction comparison problem, you'll be well-equipped to tackle it with confidence.
Latest Posts
Latest Posts
-
Make An Expression A Perfect Square
Sep 09, 2025
-
Rewrite The Inequality Without Absolute Value Bars
Sep 09, 2025
-
Which Of The Following Is Not A Valid Probability
Sep 09, 2025
-
How Do You Write A Fable
Sep 09, 2025
-
8 Is Subtracted From The Cube Of A Number
Sep 09, 2025
Related Post
Thank you for visiting our website which covers about What Is Greater 1 2 Or 2 3 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.