What Is 1 4 Of 3 4 As A Fraction
faraar
Sep 16, 2025 · 5 min read
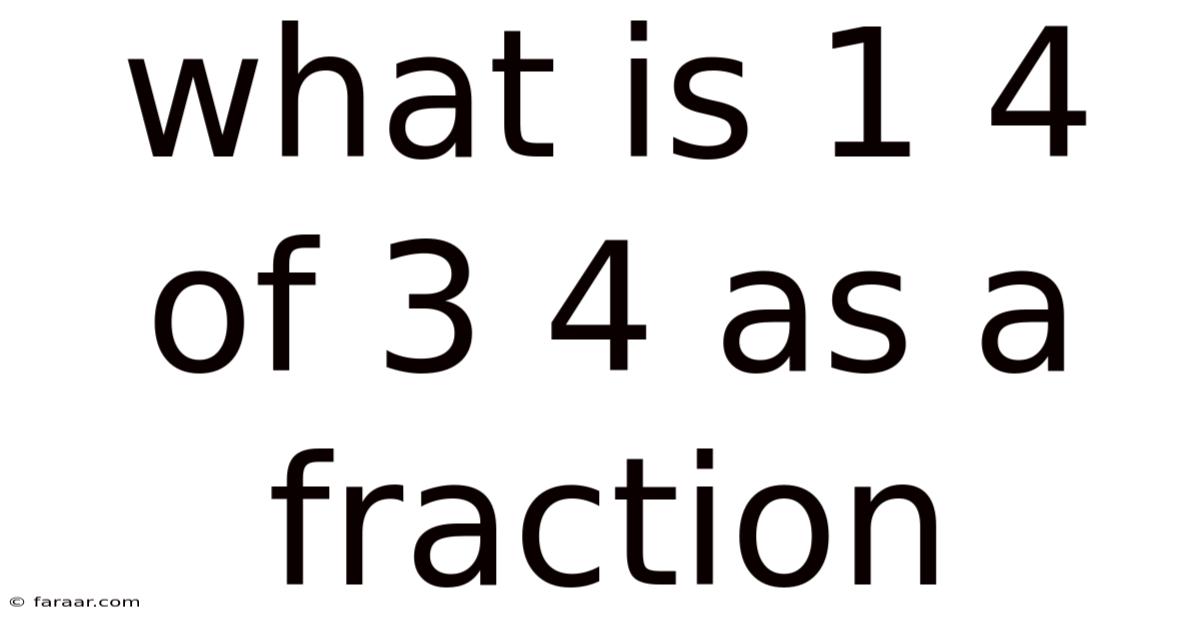
Table of Contents
What is 1/4 of 3/4 as a Fraction? A Comprehensive Guide
Finding a fraction of another fraction might seem daunting at first, but it's a fundamental concept in mathematics with widespread applications. This article will guide you through understanding what 1/4 of 3/4 is as a fraction, providing a step-by-step explanation, exploring the underlying mathematical principles, and addressing common queries. We'll demystify this seemingly complex operation, making it easily comprehensible for learners of all levels. By the end, you'll not only know the answer but also possess a solid understanding of how to tackle similar problems confidently.
Understanding the Problem: 1/4 of 3/4
The question "What is 1/4 of 3/4 as a fraction?" essentially asks us to calculate one-quarter (1/4) of three-quarters (3/4). In mathematical terms, this translates to multiplying the two fractions together: (1/4) x (3/4). This is a common operation in various fields, from calculating proportions in cooking recipes to determining percentages in financial analysis. Mastering this skill is essential for building a strong foundation in mathematics.
Step-by-Step Calculation: Multiplying Fractions
Multiplying fractions is a straightforward process. Here's how to solve (1/4) x (3/4):
-
Multiply the numerators: The numerators are the top numbers in the fractions. In this case, we multiply 1 by 3, which equals 3.
-
Multiply the denominators: The denominators are the bottom numbers in the fractions. Here, we multiply 4 by 4, which equals 16.
-
Form the new fraction: The result of multiplying the numerators becomes the numerator of the new fraction, and the result of multiplying the denominators becomes the denominator. Therefore, (1/4) x (3/4) = 3/16.
Therefore, 1/4 of 3/4 is 3/16.
Visualizing the Solution
Imagine a square divided into four equal parts. Each part represents 1/4 of the whole square. Now, imagine shading three of these four parts, representing 3/4 of the square. To find 1/4 of this shaded area (3/4), we need to divide the shaded area into four equal sections. Each of these smaller sections will represent 3/16 of the entire square.
Simplifying Fractions
Once we've calculated our answer, it's crucial to check if the fraction can be simplified. A fraction is simplified when the numerator and denominator have no common factors other than 1. In this case, 3 and 16 have no common factors other than 1, so the fraction 3/16 is already in its simplest form.
Mathematical Principles at Play
The multiplication of fractions relies on several core mathematical concepts:
-
Multiplication as Repeated Addition: Multiplication can be viewed as repeated addition. For example, 3 x 4 means adding 4 three times (4 + 4 + 4 = 12). Similarly, (1/4) x (3/4) can be interpreted as adding 3/4 one-quarter of a time.
-
Commutative Property of Multiplication: The order in which you multiply fractions doesn't affect the outcome. (1/4) x (3/4) is the same as (3/4) x (1/4).
-
Associative Property of Multiplication: When multiplying more than two fractions, you can group them in any way you like without changing the outcome. For instance, (1/2) x (1/4) x (3/2) = [(1/2) x (1/4)] x (3/2) = (1/2) x [(1/4) x (3/2)].
-
Distributive Property of Multiplication over Addition: This property is useful when dealing with more complex expressions involving fractions and addition. For example, a/b * (c/d + e/f) = (a/b * c/d) + (a/b * e/f).
Understanding these principles provides a deeper insight into the mechanics of fraction multiplication and extends your ability to solve more intricate mathematical problems.
Extending the Concept: Fractions of Fractions in Real-World Applications
The concept of finding a fraction of another fraction is incredibly practical and applies to numerous real-world scenarios:
-
Cooking and Baking: Adjusting recipes to serve more or fewer people often involves calculating fractions of fractions.
-
Financial Calculations: Determining percentages of amounts, such as interest or discounts, relies on fraction multiplication.
-
Construction and Engineering: Precise measurements and calculations in construction and engineering often involve fractions.
-
Data Analysis: Working with proportions and ratios in datasets necessitates understanding fraction multiplication.
-
Probability and Statistics: Calculating probabilities often involves finding fractions of fractions.
Frequently Asked Questions (FAQ)
Q: Can I convert the fractions to decimals before multiplying?
A: Yes, you can. Converting 1/4 to 0.25 and 3/4 to 0.75 and then multiplying them (0.25 x 0.75 = 0.1875) will give you the decimal equivalent of 3/16. However, working directly with fractions is often simpler, especially when dealing with complex fractions.
Q: What if the fractions were more complicated, such as (5/8) x (7/12)?
A: The process remains the same. Multiply the numerators together (5 x 7 = 35) and the denominators together (8 x 12 = 96). This gives you 35/96. Then simplify the fraction if possible by finding the greatest common divisor of the numerator and denominator. In this case, 35/96 is already in its simplest form.
Q: How do I handle mixed numbers (a whole number and a fraction) in a similar calculation?
A: Before multiplying, convert any mixed numbers into improper fractions. For example, 1 1/2 becomes (3/2). Then, follow the same multiplication procedure as outlined above.
Q: Why is it important to simplify fractions?
A: Simplifying fractions makes the answer easier to understand and work with. It presents the answer in its most concise and manageable form. It also helps avoid errors in subsequent calculations.
Q: Are there any online tools or calculators to help with fraction multiplication?
A: Yes, many online calculators are readily available that can assist with fraction multiplication and simplification. These tools can be particularly helpful when dealing with more complex fractions. However, understanding the underlying principles is crucial for developing a strong mathematical foundation.
Conclusion
Finding a fraction of another fraction is a fundamental mathematical operation with far-reaching applications. Through a step-by-step process of multiplying the numerators and denominators, we determined that 1/4 of 3/4 is 3/16. This calculation demonstrates the straightforward nature of fraction multiplication, emphasizing the importance of understanding the underlying mathematical principles for solving similar problems. By practicing these methods, you can confidently tackle more complex calculations and further develop your mathematical skills. Remember to always check for simplification opportunities to present your answer in its most efficient form.
Latest Posts
Latest Posts
-
A Roller Coaster Car Rapidly Picks Up Speed
Sep 16, 2025
-
In A Chemical Reaction What Are The Reactants And Products
Sep 16, 2025
-
What Is The Least Common Multiple Of 6 And 24
Sep 16, 2025
-
How Do You Solve Fraction Word Problems
Sep 16, 2025
-
What Is Bigger 1 2 Or 2 3
Sep 16, 2025
Related Post
Thank you for visiting our website which covers about What Is 1 4 Of 3 4 As A Fraction . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.