What Is Bigger 1 2 Or 2 3
faraar
Sep 16, 2025 · 5 min read
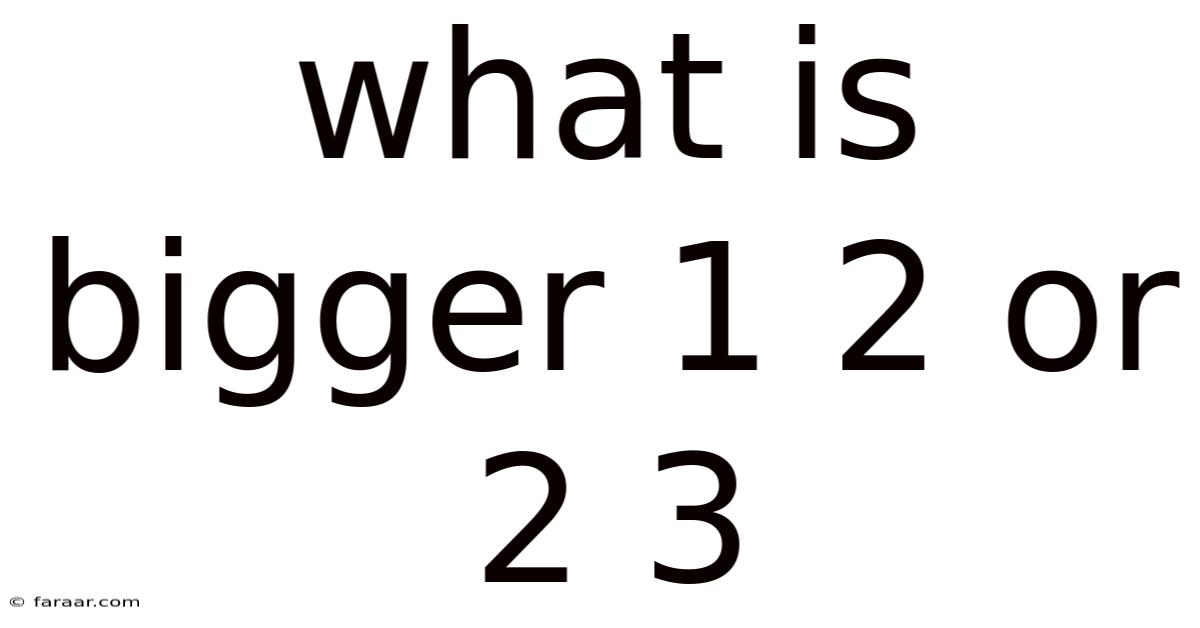
Table of Contents
Unpacking the Magnitude: A Deep Dive into Comparing 1/2 and 2/3
This article explores the seemingly simple yet conceptually rich comparison of the fractions 1/2 and 2/3. We will delve beyond a simple numerical comparison to understand the underlying mathematical principles, explore different methods for comparison, and even touch upon the broader implications of fractional understanding in mathematics and beyond. This detailed analysis aims to provide a comprehensive understanding suitable for students of various levels, from elementary school to those refreshing their mathematical foundations.
Introduction: The Foundation of Fractional Comparison
At first glance, comparing 1/2 and 2/3 might seem trivial. However, a robust understanding of fractions is crucial for building a solid mathematical foundation. This comparison necessitates a deeper understanding of concepts such as numerators, denominators, equivalent fractions, and different methods for comparing fractions. Mastering these concepts opens doors to more advanced mathematical concepts and problem-solving skills. This article serves as a thorough guide, demystifying the process and highlighting the importance of this seemingly basic comparison.
Method 1: Finding a Common Denominator
The most common and arguably the most straightforward method for comparing fractions is to find a common denominator. This involves transforming the fractions into equivalent fractions that share the same denominator.
-
Step 1: Identify the denominators: The denominators of our fractions are 2 and 3.
-
Step 2: Find the least common multiple (LCM): The LCM of 2 and 3 is 6. This means we will convert both fractions to have a denominator of 6.
-
Step 3: Convert the fractions:
- To convert 1/2 to a fraction with a denominator of 6, we multiply both the numerator and the denominator by 3: (1 x 3) / (2 x 3) = 3/6
- To convert 2/3 to a fraction with a denominator of 6, we multiply both the numerator and the denominator by 2: (2 x 2) / (3 x 2) = 4/6
-
Step 4: Compare the numerators: Now that both fractions have the same denominator, we can directly compare their numerators. Since 3 < 4, we conclude that 3/6 < 4/6.
-
Step 5: State the conclusion: Therefore, 1/2 < 2/3.
Method 2: Using Decimal Equivalents
Another effective method involves converting the fractions to their decimal equivalents. This method is particularly useful when dealing with more complex fractions or when a numerical comparison is preferred.
-
Step 1: Convert the fractions to decimals:
- 1/2 = 0.5
- 2/3 = 0.666... (a repeating decimal)
-
Step 2: Compare the decimals: By comparing the decimal values, it’s clear that 0.5 < 0.666...
-
Step 3: State the conclusion: Therefore, 1/2 < 2/3.
Method 3: Visual Representation using Fraction Bars
Visual representations are extremely helpful, especially for younger learners. Using fraction bars or diagrams can provide a clear and intuitive understanding of the comparison.
Imagine two identical bars representing a whole.
-
Representing 1/2: Divide one bar into two equal parts and shade one part. This represents 1/2.
-
Representing 2/3: Divide the other bar into three equal parts and shade two parts. This represents 2/3.
By visually comparing the shaded areas, it becomes evident that the shaded area representing 2/3 is larger than the shaded area representing 1/2. This confirms that 1/2 < 2/3.
Method 4: Cross-Multiplication
Cross-multiplication offers a slightly more advanced but efficient method for comparing fractions.
-
Step 1: Cross-multiply: Multiply the numerator of the first fraction by the denominator of the second fraction (1 x 3 = 3). Then, multiply the numerator of the second fraction by the denominator of the first fraction (2 x 2 = 4).
-
Step 2: Compare the products: Compare the two products. Since 3 < 4, the fraction with the smaller product (1/2) is the smaller fraction.
-
Step 3: State the conclusion: Therefore, 1/2 < 2/3.
The Importance of Understanding Fractions
The comparison of 1/2 and 2/3 might appear elementary, but the underlying principles are fundamental to various mathematical concepts. A solid grasp of fractions is crucial for:
-
Algebra: Solving equations and inequalities involving fractions is a core component of algebra.
-
Geometry: Calculating areas, volumes, and proportions often involves fractional calculations.
-
Calculus: Understanding limits and derivatives heavily relies on a strong foundation in fractions.
-
Real-world applications: Fractions are used in everyday life, from cooking and measuring to budgeting and finance. Understanding fractions allows for accurate calculations and informed decision-making in various situations.
Beyond the Basics: Exploring Equivalent Fractions
The concept of equivalent fractions is central to understanding fraction comparisons. Equivalent fractions represent the same value but have different numerators and denominators. For instance, 1/2, 2/4, 3/6, and 4/8 are all equivalent fractions. Understanding this concept allows for flexibility in choosing the most convenient representation for a given problem.
Frequently Asked Questions (FAQ)
Q: Can I use a calculator to compare fractions?
A: Yes, you can convert fractions to decimals using a calculator and then compare the decimal values. However, understanding the underlying methods of comparison is crucial for building mathematical proficiency.
Q: Why is finding a common denominator important?
A: Finding a common denominator allows for a direct comparison of the numerators, providing a simple and unambiguous way to determine which fraction is larger.
Q: Are there other methods to compare fractions besides the ones mentioned?
A: While the methods described are the most common and practical, other methods exist, often involving more advanced mathematical concepts.
Q: What if the fractions are negative?
A: The same principles apply, but remember that negative fractions follow the order of magnitude in reverse. For instance, -1/2 > -2/3.
Conclusion: Mastering Fractions for Future Success
Comparing 1/2 and 2/3 is more than a simple arithmetic exercise; it’s a gateway to understanding fundamental mathematical concepts. Mastering fractions is not merely about getting the right answer; it's about developing a deep understanding of numerical relationships and building a strong foundation for more advanced mathematical explorations. Through the various methods explored in this article—finding a common denominator, using decimal equivalents, visual representation, and cross-multiplication—we have thoroughly examined this seemingly simple comparison. This deep dive serves as a valuable tool for students and anyone seeking to strengthen their mathematical understanding and confidence. Remember, the journey to mathematical fluency is built upon understanding the fundamentals, and comparing fractions like 1/2 and 2/3 is an excellent starting point for this journey.
Latest Posts
Latest Posts
-
How Many Pounds Is 600 G
Sep 16, 2025
-
Find The Area Of The Region Bounded By The
Sep 16, 2025
-
How To Identify Zero Force Members In A Truss
Sep 16, 2025
-
8 Less Than 3 Times X
Sep 16, 2025
-
Is 1 4 Half Of 1 2 Cup
Sep 16, 2025
Related Post
Thank you for visiting our website which covers about What Is Bigger 1 2 Or 2 3 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.