What Is The Least Common Multiple Of 6 And 24
faraar
Sep 16, 2025 · 6 min read
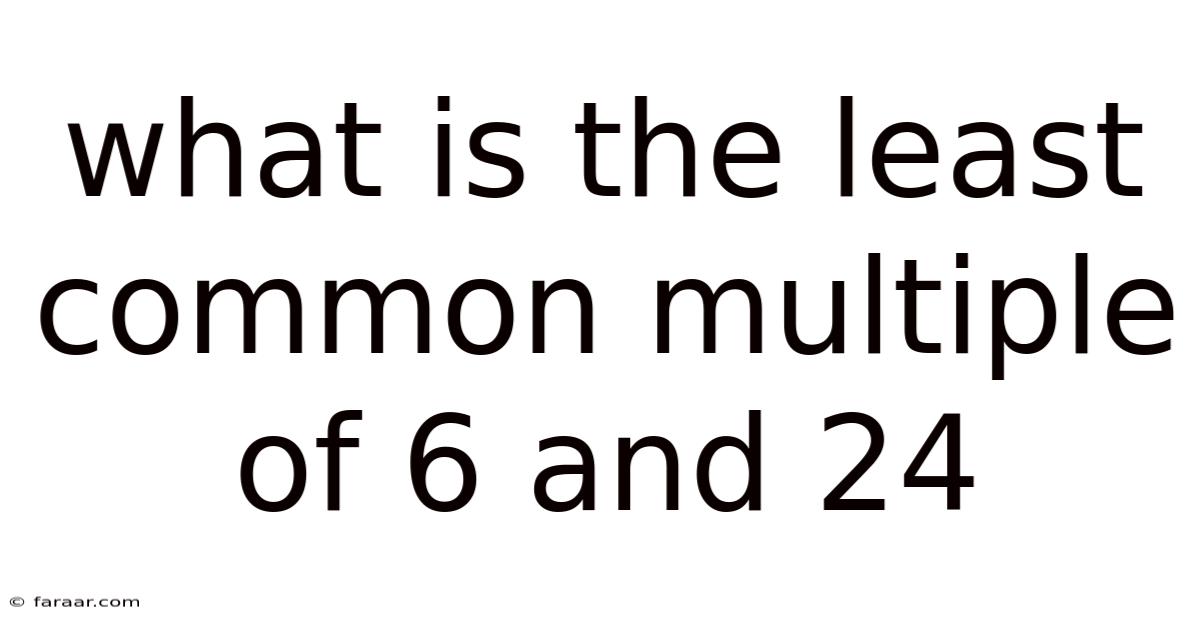
Table of Contents
Unveiling the Least Common Multiple (LCM) of 6 and 24: A Deep Dive into Number Theory
Finding the least common multiple (LCM) might seem like a simple arithmetic task, but understanding the underlying principles unlocks a deeper appreciation for number theory and its applications in various fields. This article will thoroughly explore how to find the LCM of 6 and 24, providing multiple methods and delving into the mathematical concepts behind them. We'll also explore the significance of LCMs in real-world scenarios and answer frequently asked questions. By the end, you’ll not only know the LCM of 6 and 24 but also possess a comprehensive understanding of this fundamental mathematical concept.
Understanding Least Common Multiple (LCM)
Before tackling the specific problem of finding the LCM of 6 and 24, let's establish a clear understanding of what an LCM actually is. The least common multiple of two or more integers is the smallest positive integer that is divisible by all the integers. In simpler terms, it's the smallest number that all the given numbers can divide into evenly without leaving a remainder.
For example, consider the numbers 2 and 3. Multiples of 2 are 2, 4, 6, 8, 10, 12... Multiples of 3 are 3, 6, 9, 12, 15... The common multiples of 2 and 3 are 6, 12, 18... The smallest of these common multiples is 6, so the LCM of 2 and 3 is 6.
Methods for Finding the LCM of 6 and 24
There are several efficient methods to determine the LCM of two numbers. We will explore three prominent techniques: listing multiples, prime factorization, and using the greatest common divisor (GCD).
1. Listing Multiples Method
This is the most straightforward method, particularly useful for smaller numbers. We list the multiples of each number until we find the smallest common multiple.
- Multiples of 6: 6, 12, 18, 24, 30, 36...
- Multiples of 24: 24, 48, 72...
By comparing the lists, we can readily see that the smallest number appearing in both lists is 24. Therefore, the LCM of 6 and 24 is 24.
This method is simple to visualize but becomes less practical as the numbers get larger.
2. Prime Factorization Method
This method leverages the fundamental theorem of arithmetic, which states that every integer greater than 1 can be uniquely represented as a product of prime numbers. The process involves:
-
Finding the prime factorization of each number:
- 6 = 2 × 3
- 24 = 2 × 2 × 2 × 3 = 2³ × 3
-
Identifying the highest power of each prime factor:
- The highest power of 2 is 2³ = 8
- The highest power of 3 is 3¹ = 3
-
Multiplying the highest powers together:
- LCM(6, 24) = 2³ × 3 = 8 × 3 = 24
This method is more efficient than listing multiples, especially for larger numbers, as it avoids extensive listing. It provides a clear and systematic approach to finding the LCM.
3. Using the Greatest Common Divisor (GCD) Method
This method utilizes the relationship between the LCM and the greatest common divisor (GCD) of two numbers. The GCD is the largest number that divides both numbers without leaving a remainder. The formula connecting LCM and GCD is:
LCM(a, b) × GCD(a, b) = a × b
-
Finding the GCD of 6 and 24:
- The factors of 6 are 1, 2, 3, 6.
- The factors of 24 are 1, 2, 3, 4, 6, 8, 12, 24.
- The greatest common factor is 6. Therefore, GCD(6, 24) = 6.
-
Applying the formula:
- LCM(6, 24) × 6 = 6 × 24
- LCM(6, 24) = (6 × 24) / 6 = 24
This method is particularly efficient when dealing with larger numbers where finding the prime factorization can be more computationally intensive. It leverages a pre-calculated GCD to directly compute the LCM.
Real-World Applications of LCM
The concept of LCM isn't just a theoretical exercise; it has numerous practical applications in various fields:
-
Scheduling: Imagine two buses depart from a station at different intervals. The LCM helps determine when both buses will depart simultaneously again.
-
Construction and Engineering: In construction projects, materials might need to be cut into specific lengths. The LCM ensures efficient utilization of materials by finding the longest common length that can be used without wastage.
-
Music Theory: The LCM plays a role in determining when different musical rhythms will synchronize.
-
Manufacturing: In manufacturing processes, machines might operate at different cycles. Determining the LCM helps optimize production schedules and minimize downtime.
-
Computer Science: LCM is used in various algorithms and data structures, such as finding the least common multiple of array elements or optimizing memory allocation.
A Deeper Dive into Number Theory: Divisibility and Factors
Understanding the LCM is intrinsically linked to the concepts of divisibility and factors. A number 'a' is divisible by a number 'b' if the division of 'a' by 'b' leaves no remainder. The factors of a number are the integers that divide it without leaving a remainder.
For instance, the factors of 6 are 1, 2, 3, and 6. The factors of 24 are 1, 2, 3, 4, 6, 8, 12, and 24. Notice that all the factors of 6 are also factors of 24. This is because 24 is a multiple of 6. The LCM considers the smallest number that contains all the prime factors of both numbers, raised to their highest powers.
Frequently Asked Questions (FAQ)
Q1: Is the LCM always greater than or equal to the larger of the two numbers?
A1: Yes, the LCM will always be greater than or equal to the larger of the two numbers. This is because the LCM must be divisible by both numbers.
Q2: What is the LCM of two prime numbers?
A2: The LCM of two prime numbers is simply their product. Since prime numbers have only two factors (1 and themselves), they don't share any common factors other than 1.
Q3: Can the LCM of two numbers be equal to one of the numbers?
A3: Yes, if one number is a multiple of the other, then the LCM will be the larger number. As we saw with 6 and 24, the LCM is 24.
Q4: How do I find the LCM of more than two numbers?
A4: You can extend the prime factorization method or the GCD method to find the LCM of more than two numbers. For prime factorization, you find the prime factorization of each number and take the highest power of each prime factor present in any of the numbers. For the GCD method, you can find the GCD of the first two numbers, then find the GCD of the result and the third number, and so on, until you've included all the numbers. Then use the formula connecting LCM and GCD to find the final LCM.
Q5: Are there any online calculators or tools to find the LCM?
A5: Yes, many online calculators and mathematical software packages can efficiently calculate the LCM of any set of numbers.
Conclusion: Mastering the LCM
Finding the least common multiple of 6 and 24, as we've demonstrated, is achievable through multiple methods: listing multiples, prime factorization, and utilizing the GCD. Understanding these methods provides a foundational understanding of number theory and its practical implications across diverse fields. While the answer to our specific question is 24, the true value lies in grasping the underlying principles and applying them to solve more complex problems involving LCMs and related concepts. This deep dive into the LCM not only provides a solution but fosters a richer appreciation for the elegance and utility of mathematics.
Latest Posts
Latest Posts
-
How To Find The Volume Of A Half Circle
Sep 16, 2025
-
If A Dog Cell Has 72 Chromosomes
Sep 16, 2025
-
How Many Pounds Is 600 G
Sep 16, 2025
-
Find The Area Of The Region Bounded By The
Sep 16, 2025
-
How To Identify Zero Force Members In A Truss
Sep 16, 2025
Related Post
Thank you for visiting our website which covers about What Is The Least Common Multiple Of 6 And 24 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.