Given Ad Bc And Bcd Adc
faraar
Sep 13, 2025 · 6 min read
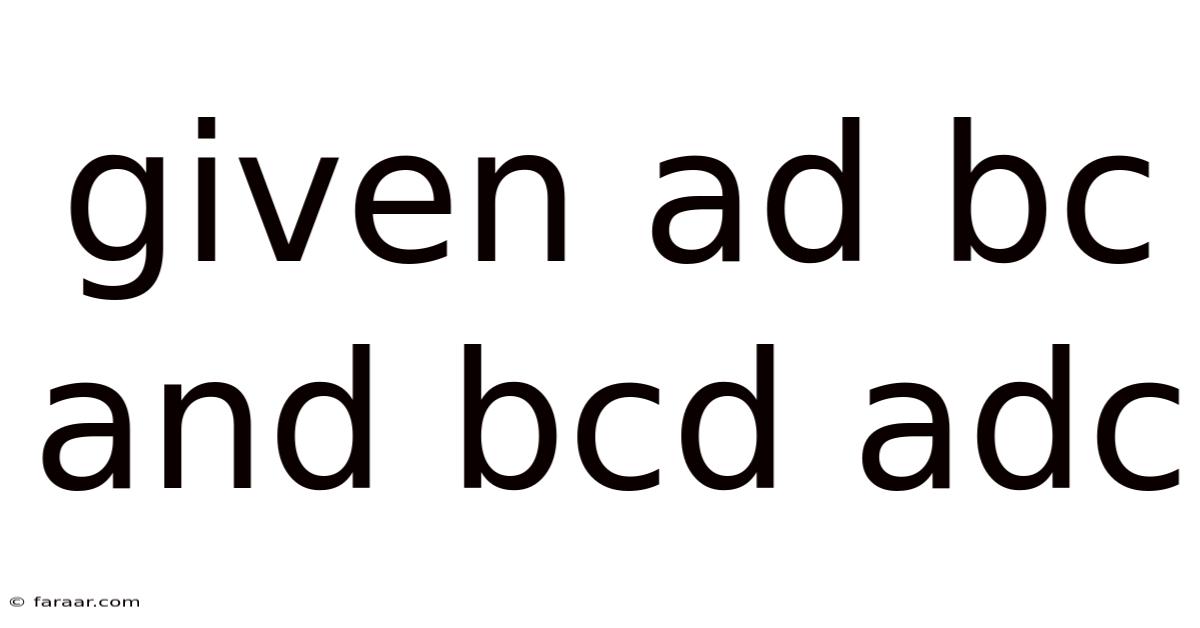
Table of Contents
Understanding Given Angles: Exploring the Relationships Between ∠ABC, ∠BCD, and ∠ADC
This article delves into the geometric relationships between three angles: ∠ABC, ∠BCD, and ∠ADC. We'll explore how these angles interact within different shapes and contexts, providing a comprehensive understanding applicable to various geometric problems. Understanding the properties and potential relationships between these angles is crucial for mastering geometry, particularly when dealing with quadrilaterals, triangles, and cyclic quadrilaterals. We'll examine scenarios where these angles are given, how to deduce other angle measures, and the underlying theorems that govern their relationships.
Introduction: The Foundation of Geometric Analysis
In geometry, identifying and utilizing relationships between angles is fundamental to problem-solving. When given angles like ∠ABC, ∠BCD, and ∠ADC, we need a systematic approach to uncover hidden connections and solve for unknown angles or properties of the shape involved. These three angles often appear in problems involving quadrilaterals, particularly cyclic quadrilaterals, where the relationships between angles are particularly interesting and powerful. This article will guide you through various scenarios, explaining how to analyze these angles and apply your knowledge effectively. The core concepts we will explore will build a strong foundation for more advanced geometrical concepts.
Scenario 1: Angles in a Quadrilateral
Let's begin with the simplest scenario: ∠ABC, ∠BCD, and ∠ADC are three angles of a quadrilateral ABCD. Remember that the sum of the interior angles of any quadrilateral is always 360°. Therefore, if we know the measures of three angles (∠ABC, ∠BCD, and ∠ADC), we can easily calculate the measure of the fourth angle (∠BAD) using the following formula:
∠BAD = 360° - (∠ABC + ∠BCD + ∠ADC)
Example: If ∠ABC = 70°, ∠BCD = 100°, and ∠ADC = 110°, then:
∠BAD = 360° - (70° + 100° + 110°) = 360° - 280° = 80°
This simple calculation highlights the fundamental relationship between interior angles within a quadrilateral. This basic principle forms the groundwork for tackling more complex problems involving these angles.
Scenario 2: Angles in a Cyclic Quadrilateral
A cyclic quadrilateral is a quadrilateral whose vertices all lie on a single circle. Cyclic quadrilaterals possess a unique property: opposite angles are supplementary (their sum is 180°). This property significantly influences the relationships between ∠ABC, ∠BCD, and ∠ADC if they are part of a cyclic quadrilateral.
Let's assume ABCD is a cyclic quadrilateral. If we are given ∠ABC and ∠BCD, we can determine ∠ADC and ∠BAD using the supplementary angle property:
- ∠ADC = 180° - ∠ABC
- ∠BAD = 180° - ∠BCD
Example: If ∠ABC = 85° and ∠BCD = 95° in a cyclic quadrilateral ABCD, then:
- ∠ADC = 180° - 85° = 95°
- ∠BAD = 180° - 95° = 85°
This reveals the symmetrical nature of opposite angles in cyclic quadrilaterals. Knowing that the quadrilateral is cyclic drastically simplifies the calculation of the unknown angles. The cyclic quadrilateral property allows us to deduce angles solely from the knowledge of two opposite angles.
Scenario 3: Angles in Adjacent Triangles
The angles ∠ABC, ∠BCD, and ∠ADC might be part of adjacent triangles sharing a common side. For example, consider triangles ABC and ADC sharing the side AC. If we know two angles in one triangle and one angle in the adjacent triangle, we can utilize the angle sum property of triangles (180°) to find unknown angles.
Suppose we know ∠ABC, ∠BAC, and ∠ADC. We can find ∠BCA using the triangle angle sum property in triangle ABC:
∠BCA = 180° - (∠ABC + ∠BAC)
Similarly, in triangle ADC, we can find ∠CAD using:
∠CAD = 180° - (∠ADC + ∠ACD) (Note: ∠ACD = ∠BCA if the points B and D are collinear)
This approach emphasizes the importance of understanding how angles in connected triangles relate. By recognizing shared sides and using the triangle angle sum rule, we can systematically solve for unknown angles within a more complex geometric figure.
Scenario 4: Angles Formed by Intersecting Lines
If the lines AB and CD intersect at a point, forming angles ∠ABC and ∠ADC, and line BC intersects with another line forming ∠BCD, then we have to consider the properties of vertically opposite angles and other angle relationships associated with intersecting lines. Vertically opposite angles are equal. If lines AB and CD intersect at a point O, then ∠AOB = ∠COD and ∠AOC = ∠BOD. However, without additional information regarding the intersection of lines, we cannot establish a direct relationship between ∠ABC, ∠BCD, and ∠ADC in this context. We need more information or constraints.
Scenario 5: Application in Coordinate Geometry
When dealing with points in a Cartesian coordinate system, we can utilize the distance formula and trigonometric functions to determine the angles. For instance, if we know the coordinates of points A, B, C, and D, we can use the dot product formula to find the cosine of the angles and subsequently calculate the angle measures. This approach can be more complex but provides a powerful tool for determining angles in a precise and computationally efficient way. This method is especially useful when dealing with precisely defined points.
The Importance of Diagrams and Visual Representation
Throughout all these scenarios, the crucial first step is to create a clear and accurate diagram. A well-drawn diagram allows for a better understanding of the problem and visual identification of potential relationships between the given angles. It aids in recognizing the shape formed by the points (quadrilateral, triangle, etc.), helping to apply the correct theorems and formulas. A visual representation can often unlock the solution more quickly than algebraic manipulation alone.
Mathematical Proof and Rigor
Many geometric problems require more than simple calculations. They often necessitate the development of a formal mathematical proof to establish a relationship between angles and other geometric properties. Such proofs usually start with the given information, apply relevant axioms, postulates, and theorems, and finally arrive at the conclusion, rigorously demonstrating the relationship. This approach is crucial for rigorous mathematical reasoning and building a comprehensive understanding of geometry.
Frequently Asked Questions (FAQ)
Q: Can ∠ABC, ∠BCD, and ∠ADC always be part of the same polygon?
A: No. They could be angles in different polygons that share a common point or line, or even be unrelated angles in separate geometric figures. The context of the problem is crucial in determining their relationship.
Q: What if some of the angles are obtuse or reflex?
A: The principles remain the same. Obtuse (greater than 90° but less than 180°) and reflex (greater than 180° but less than 360°) angles are still subject to the angle sum properties of polygons and the relationships discussed above. Remember to account for their specific values when calculating sums or differences.
Q: How can I improve my problem-solving skills in this area?
A: Consistent practice is key. Work through various problems of increasing complexity, focusing on visualizing the geometry and applying the appropriate theorems. Regularly reviewing fundamental geometric principles will also improve your ability to recognize and solve more complex scenarios.
Conclusion: Mastering Angular Relationships
Understanding the relationships between ∠ABC, ∠BCD, and ∠ADC hinges on recognizing the geometric context. Whether they're angles within a quadrilateral, cyclic quadrilateral, adjacent triangles, or even formed by intersecting lines, applying the correct theorems and principles—such as the angle sum of polygons, supplementary angles in cyclic quadrilaterals, and the angle sum of triangles—is crucial. The ability to systematically analyze these angles and uncover their connections is a cornerstone of geometric proficiency. Remember to always start with a clear diagram and apply rigorous mathematical reasoning to arrive at accurate and well-supported solutions. Mastering these concepts provides a robust foundation for tackling more advanced geometry problems. Through practice and consistent application of principles, you can build confidence and skill in solving increasingly complex geometric challenges involving these angles and many others.
Latest Posts
Latest Posts
-
Compute Displaystyle Left Frac 8 125 Right 1 3
Sep 13, 2025
-
Closed Circle Vs Open Circle Graph
Sep 13, 2025
-
How Do You Find Slope In Standard Form
Sep 13, 2025
-
How To Calculate H3o From Ph
Sep 13, 2025
-
According To Bronsted Lowry Theory A Base Is
Sep 13, 2025
Related Post
Thank you for visiting our website which covers about Given Ad Bc And Bcd Adc . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.