Find 2 Consecutive Even Integers Whose Sum Is 126
faraar
Sep 22, 2025 · 5 min read
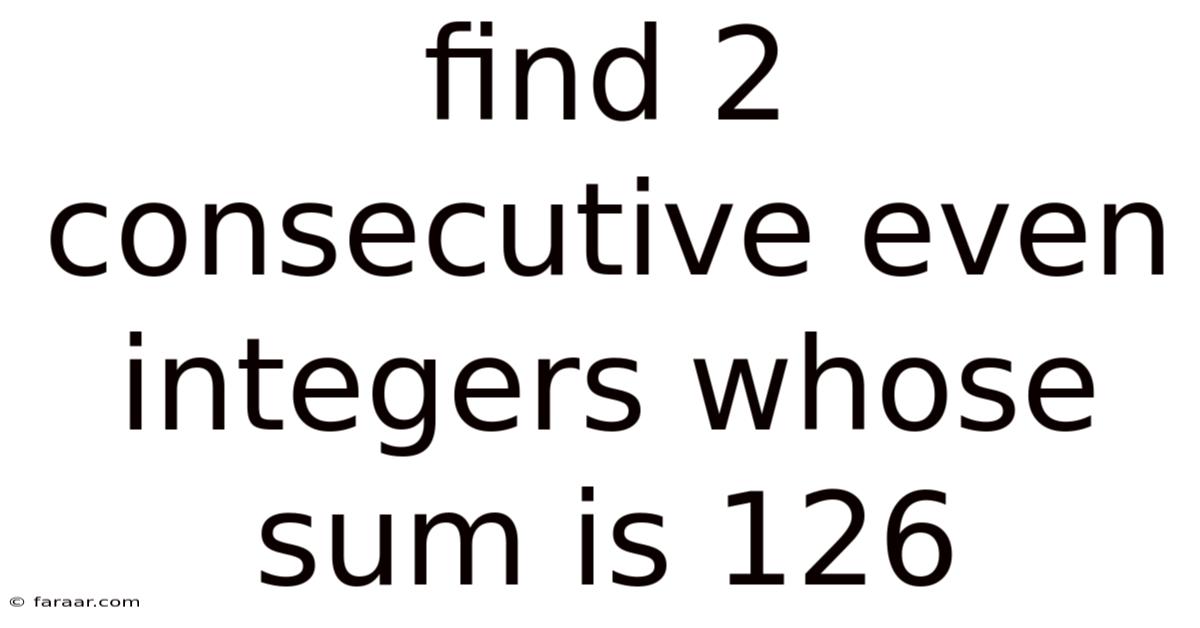
Table of Contents
Finding Consecutive Even Integers: A Comprehensive Guide
Finding consecutive even integers whose sum equals a specific number is a common problem in elementary algebra. This article will not only guide you through solving the problem of finding two consecutive even integers that sum to 126 but also provide a deeper understanding of the underlying mathematical principles, explore different solution methods, and delve into related problems. We’ll cover everything from basic algebraic techniques to more advanced approaches, ensuring a comprehensive understanding for learners of all levels.
Understanding the Problem: Consecutive Even Integers
The core of this problem lies in understanding the concept of "consecutive even integers." Consecutive simply means numbers that follow each other without any gaps. Even integers are whole numbers divisible by 2 (e.g., 2, 4, 6, 8...). Therefore, consecutive even integers are even numbers that follow each other, such as 2 and 4, 10 and 12, or 100 and 102. Our challenge is to find two such numbers that add up to 126.
Method 1: The Algebraic Approach
This is the most common and straightforward method. We can represent the problem algebraically:
- Let 'x' represent the first even integer. Since we are dealing with consecutive even integers, the next even integer will be 'x + 2'.
Now, we can translate the problem into an equation:
- x + (x + 2) = 126
This equation states that the sum of the first even integer ('x') and the next consecutive even integer ('x + 2') equals 126.
Let's solve this equation:
- Combine like terms: 2x + 2 = 126
- Subtract 2 from both sides: 2x = 124
- Divide both sides by 2: x = 62
Therefore, the first even integer is 62. The next consecutive even integer is x + 2 = 62 + 2 = 64.
Solution: The two consecutive even integers are 62 and 64. Let's check our answer: 62 + 64 = 126. Our solution is correct.
Method 2: The Intuitive Approach (Trial and Error)
While the algebraic method is precise and efficient, for smaller numbers, an intuitive approach using trial and error can also work. We know the two numbers must be close to half of 126 (which is 63). Since we need even numbers, we can try numbers around 63:
- 60 + 62 = 122 (Too low)
- 62 + 64 = 126 (Correct!)
This method is quicker for simple problems but becomes less practical as the target sum increases.
Method 3: Using Arithmetic Sequences
Consecutive even integers form an arithmetic sequence where the common difference between terms is 2. We can utilize the formula for the sum of an arithmetic series:
- S<sub>n</sub> = n/2 [2a + (n - 1)d]
Where:
- S<sub>n</sub> is the sum of the series (126 in our case)
- n is the number of terms (2 in our case)
- a is the first term (which we need to find)
- d is the common difference (2 in our case)
Substituting our values:
126 = 2/2 [2a + (2 - 1)2] 126 = 2a + 2 124 = 2a a = 62
This confirms that the first term (the first even integer) is 62, and the next consecutive even integer is 64.
Extending the Problem: More Than Two Consecutive Even Integers
The methods described above can be adapted to find more than two consecutive even integers. For example, let's say we need to find three consecutive even integers that add up to 126.
We can represent the integers as: x, x + 2, and x + 4.
The equation becomes: x + (x + 2) + (x + 4) = 126
Solving this equation:
- Combine like terms: 3x + 6 = 126
- Subtract 6 from both sides: 3x = 120
- Divide both sides by 3: x = 40
Therefore, the three consecutive even integers are 40, 42, and 44. Let's check: 40 + 42 + 44 = 126.
Solving for Odd Consecutive Integers
The principles remain the same if we're dealing with consecutive odd integers. For example, to find two consecutive odd integers that add up to 126, we would represent them as x and x + 2 (the difference between consecutive odd integers is also 2). The solution process would follow the same algebraic steps as shown above.
The Importance of Understanding the Underlying Principles
The ability to solve problems involving consecutive even or odd integers is not just about finding the numerical answer. It demonstrates a crucial understanding of:
- Algebraic representation: Translating word problems into mathematical equations.
- Equation solving: Mastering the techniques to solve linear equations.
- Number patterns and sequences: Recognizing and utilizing patterns in number series.
- Problem-solving strategies: Choosing the most appropriate method based on the problem's complexity.
Frequently Asked Questions (FAQs)
Q: Can I use negative even integers?
A: Yes, absolutely. The methods outlined above apply equally to negative even integers. For example, if the sum were a negative number, you would find negative even integers as a solution.
Q: What if the sum is an odd number?
A: It's impossible to find two consecutive even integers that add up to an odd number. The sum of two even integers is always even.
Q: How can I solve this problem using a computer program?
A: You can easily write a simple program (in Python, Java, or any other language) to iterate through even numbers and check their sums until the target sum is found.
Q: Are there any real-world applications of this type of problem?
A: While this might seem like a purely mathematical exercise, the underlying principles are applicable in various fields, including:
- Inventory management: Calculating stock levels or orders based on even or odd quantities.
- Scheduling and resource allocation: Optimizing tasks or assigning resources in even or odd intervals.
- Data analysis: Identifying patterns and sequences in numerical datasets.
Conclusion: Mastering the Fundamentals
Finding consecutive even integers whose sum equals a specific number is a fundamental problem that reinforces key algebraic concepts. Mastering this type of problem builds a solid foundation for more advanced mathematical studies. Remember that understanding the underlying principles is as important as finding the correct answer. By utilizing the algebraic approach, the intuitive approach, or the arithmetic sequence method, you can efficiently solve such problems and extend your understanding to similar challenges involving consecutive odd integers or a larger number of terms. The key is to practice and apply the methods in various contexts to solidify your understanding.
Latest Posts
Latest Posts
-
343 To The Power Of 1 3
Sep 22, 2025
-
What Element Has The Symbol 0
Sep 22, 2025
-
A Super Dart Of Mass 20g
Sep 22, 2025
-
How Many Pounds Of Potato Salad For 50
Sep 22, 2025
-
What Is The Northernmost State In The Us
Sep 22, 2025
Related Post
Thank you for visiting our website which covers about Find 2 Consecutive Even Integers Whose Sum Is 126 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.