4 Is Subtracted From The Square Of A Number
faraar
Sep 22, 2025 · 5 min read
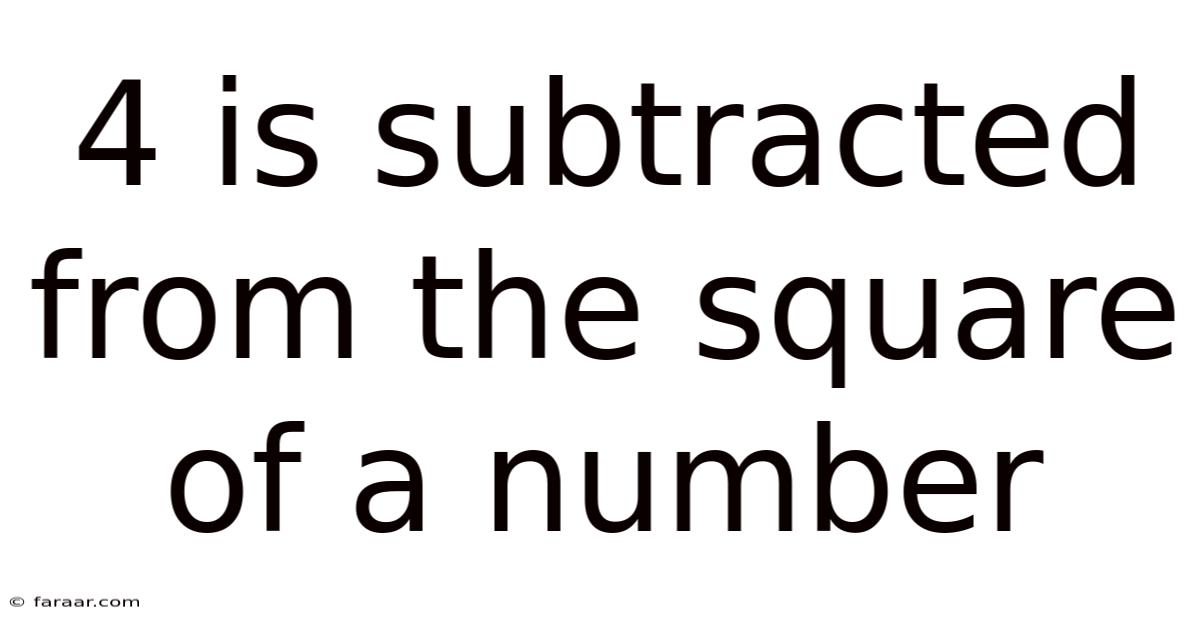
Table of Contents
Exploring the Equation: 4 Subtracted from the Square of a Number
This article delves into the mathematical expression "4 subtracted from the square of a number," exploring its various interpretations, solutions, and applications. We'll unpack the underlying concepts, demonstrate how to solve related problems, and address common misconceptions. Understanding this seemingly simple equation opens doors to more complex algebraic manipulations and problem-solving strategies. We'll cover everything from basic algebra to more advanced considerations, making this a comprehensive guide suitable for students and enthusiasts alike.
Understanding the Equation: x² - 4
The core of our exploration is the algebraic expression: x² - 4. This represents the operation of subtracting 4 from the square of a variable, x. The variable x can represent any real number. The square of a number (x²) is the result of multiplying the number by itself (x * x). The expression simplifies mathematical descriptions of various real-world scenarios, from calculating areas to modeling physical phenomena.
Keywords: x² - 4, quadratic expression, algebra, factoring, difference of squares, solving equations, roots, parabola.
Solving x² - 4 = 0
Let's start with a fundamental case: x² - 4 = 0. This equation asks: "What number, when squared and then has 4 subtracted, equals zero?" To solve this, we can use several methods:
1. Factoring: This is often the quickest and most elegant method. Notice that x² - 4 is a difference of squares. The difference of squares formula states that a² - b² = (a + b)(a - b). In our case, a = x and b = 2. Therefore:
x² - 4 = (x + 2)(x - 2) = 0
This means either (x + 2) = 0 or (x - 2) = 0. Solving these gives us two solutions:
- x = -2
- x = 2
2. Using the Square Root Property: We can rearrange the equation:
x² = 4
Taking the square root of both sides gives:
x = ±√4
x = ±2
This method directly yields both positive and negative solutions.
3. Quadratic Formula: While overkill for this simple equation, the quadratic formula is a powerful tool for solving any quadratic equation of the form ax² + bx + c = 0. In our case, a = 1, b = 0, and c = -4. The quadratic formula is:
x = [-b ± √(b² - 4ac)] / 2a
Substituting our values:
x = [0 ± √(0² - 4 * 1 * -4)] / 2 * 1
x = ±√16 / 2
x = ±4 / 2
x = ±2
All three methods arrive at the same solutions: x = 2 and x = -2. These are the roots or zeros of the equation.
Graphical Representation: The Parabola
The equation y = x² - 4 represents a parabola, a U-shaped curve. Plotting this equation reveals the roots we found algebraically. The parabola intersects the x-axis (where y = 0) at x = -2 and x = 2, confirming our solutions. The vertex of the parabola, its lowest point, is at (0, -4). Understanding the graphical representation provides a visual interpretation of the equation's behavior.
Solving x² - 4 = k (where k is a constant)
Let's generalize the problem. Instead of x² - 4 = 0, let's consider x² - 4 = k, where k is any constant. The solution method remains similar:
x² = k + 4
x = ±√(k + 4)
The solutions depend entirely on the value of k.
- If k + 4 > 0: There will be two real solutions.
- If k + 4 = 0: There will be one real solution (x = 0).
- If k + 4 < 0: There will be no real solutions; the solutions will be imaginary numbers involving the imaginary unit i (where i² = -1).
Real-World Applications
The equation x² - 4, or variations of it, appears in numerous real-world scenarios:
-
Area Calculations: Imagine a square with sides of length (x + 2) and (x - 2). The area of the square is (x + 2)(x - 2) = x² - 4. Setting this equal to a specific area allows us to find the side length x.
-
Physics: In physics, equations involving squares often describe relationships between variables like distance, velocity, and time. Subtracting a constant might represent a starting condition or a force acting against motion.
-
Engineering: Similar to physics, engineering problems involving forces, stresses, and strains may utilize quadratic equations with similar structures.
Frequently Asked Questions (FAQ)
Q: What if the equation is 4 - x² = 0?
A: This is simply a rearrangement of our original equation. Solving 4 - x² = 0 is equivalent to solving x² - 4 = 0, yielding the same solutions: x = 2 and x = -2.
Q: Can this equation be solved graphically using a calculator or software?
A: Yes, graphing calculators and mathematical software (like GeoGebra or Desmos) can easily plot the function y = x² - 4 and visually identify the x-intercepts (the points where the graph crosses the x-axis), which represent the solutions to the equation x² - 4 = 0.
Q: What are imaginary numbers and how do they relate to this equation?
A: If k (in the equation x² - 4 = k) results in a negative value inside the square root (√(k+4)), the solutions become imaginary numbers. Imaginary numbers involve the imaginary unit i, where i² = -1. For example, if k = -5, then x = ±√(-1) = ±i. These solutions have no real-world geometric representation on a standard x-y plane but are crucial in advanced mathematics and physics.
Q: Are there more complex variations of this equation?
A: Yes, consider equations like (x - a)² - 4 = 0, where 'a' is a constant. This shifts the parabola horizontally. More complex quadratic equations with terms like bx and a constant c (ax² + bx + c = 0) require the quadratic formula or other methods for solving.
Conclusion
The seemingly simple equation "4 subtracted from the square of a number" provides a gateway to understanding fundamental algebraic concepts, from factoring and solving quadratic equations to interpreting graphical representations. Through factoring, the square root property, and the quadratic formula, we can efficiently find the solutions. This simple equation has far-reaching applications in various fields, highlighting the power of basic mathematical principles in solving complex real-world problems. By mastering these concepts, you build a strong foundation for tackling more advanced mathematical challenges. Remember to practice solving various variations of this equation to solidify your understanding and develop your problem-solving skills.
Latest Posts
Latest Posts
-
How Can A Signal Be Amplified During Signal Transduction
Sep 22, 2025
-
4 1 2 5 1 2
Sep 22, 2025
-
How Much Sour Cream Is A Pint
Sep 22, 2025
-
Two Lines Orthogonal To A Third Line Are Parallel
Sep 22, 2025
-
Oxidation Number Of P In Po4 3
Sep 22, 2025
Related Post
Thank you for visiting our website which covers about 4 Is Subtracted From The Square Of A Number . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.