4 1 2 5 1 2
faraar
Sep 22, 2025 · 7 min read
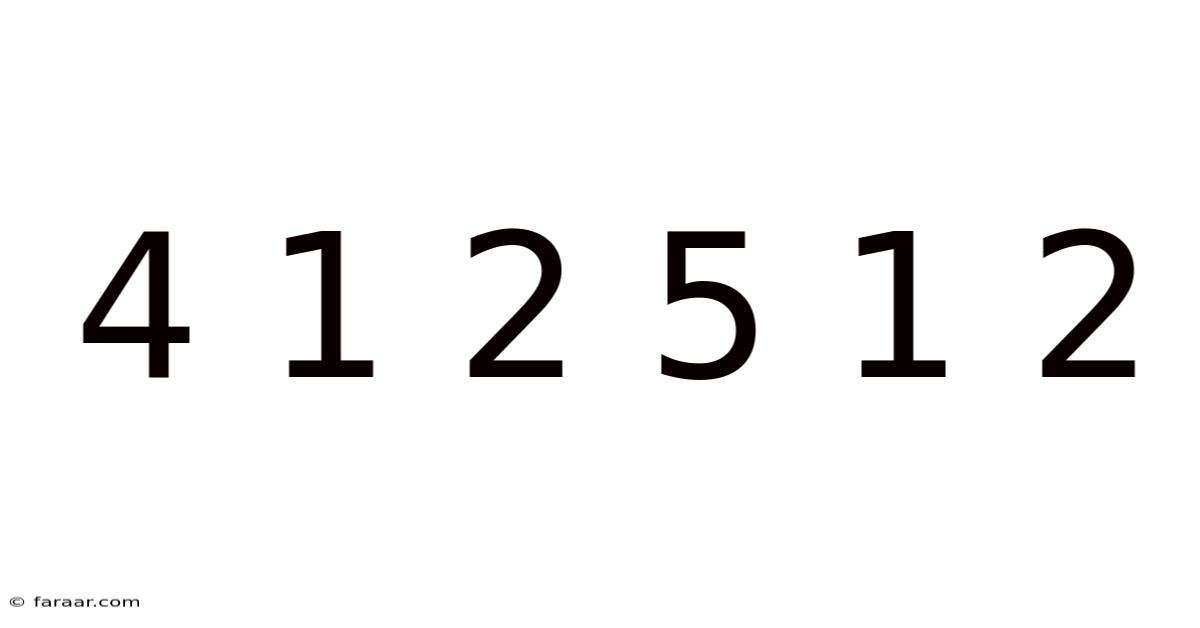
Table of Contents
Decoding the Sequence: Unveiling the Mysteries Behind 4 1 2 5 1 2
The seemingly simple sequence "4 1 2 5 1 2" might appear innocuous at first glance. However, this numerical arrangement holds a fascinating potential for deeper analysis, depending on the context in which it's presented. This article delves into various perspectives, exploring possible interpretations, mathematical patterns, and the importance of context in decoding such sequences. We'll journey from simple observation to complex analysis, uncovering the potential hidden meanings and applications of this intriguing number pattern.
Introduction: The Allure of Numerical Sequences
Numerical sequences, patterns of numbers arranged in a specific order, have captivated mathematicians and puzzle enthusiasts for centuries. From the Fibonacci sequence to prime numbers, these patterns often reveal underlying mathematical principles and structures. The sequence "4 1 2 5 1 2," while seemingly less famous than others, presents a unique opportunity to explore different analytical approaches and appreciate the beauty of mathematical discovery. Understanding this sequence can sharpen our observation skills and introduce us to the fundamental principles of pattern recognition.
Possible Interpretations: Context is Key
The true meaning of "4 1 2 5 1 2" depends entirely on its context. Without additional information, multiple interpretations are possible. Let's explore some:
1. A Random Sequence:
The most straightforward interpretation is that the sequence is simply random. There's no inherent mathematical relationship between the numbers. This possibility shouldn't be dismissed, as randomness is a fundamental concept in many fields, including statistics and cryptography. In the absence of further data, assuming randomness is a valid starting point.
2. A Code or Cipher:
The sequence could represent a code or cipher. Numbers can be used to represent letters, symbols, or even musical notes. To decipher it, we would need a key or additional information. For example, a simple substitution cipher, using a numeric alphabet, could unlock its meaning. Consider the possibility of a more complex cipher requiring knowledge of cryptographic techniques.
3. A Measurement or Observation:
The numbers could represent measurements or observations in a scientific experiment, a real-world phenomenon, or an engineering process. Each number might represent a different parameter or stage in a process. Understanding the units of measurement and the context of the observation is crucial to interpreting the significance of the data.
4. A Mathematical Puzzle:
The sequence might be part of a larger mathematical puzzle or problem. It could be a clue, a fragment of a larger pattern, or a stepping stone to a more complex sequence. Determining the type of mathematical operation involved – arithmetic, geometric, or another more intricate process – is vital to solving the puzzle.
Exploring Mathematical Patterns: The Search for Structure
If we assume the sequence isn't purely random, we can explore potential mathematical relationships. Let’s consider some possibilities:
1. Arithmetic Progression:
An arithmetic progression is a sequence where the difference between consecutive terms is constant. In this case, the differences are not constant (3, -1, 3, -4, 1), indicating this isn't an arithmetic progression.
2. Geometric Progression:
A geometric progression is a sequence where the ratio between consecutive terms is constant. Again, this is not the case here, as the ratios vary considerably.
3. Fibonacci-like Sequences:
Fibonacci sequences are characterized by each number being the sum of the two preceding numbers. While "4 1 2 5 1 2" doesn't directly fit this pattern, we can explore variations. We might find a modified Fibonacci-type sequence with different starting values or a slightly altered addition rule that produces similar results. Exploring variations on well-known mathematical patterns can be revealing.
4. Modular Arithmetic:
Modular arithmetic involves working with remainders after division. We can investigate if the sequence exhibits patterns within a specific modulus. For example, examining the remainders when each number is divided by a particular integer might unveil hidden structure. Experimentation with different moduli is necessary to discover potential patterns.
5. Recursive Relationships:
Recursive relationships define a sequence by relating each term to previous terms. We could attempt to formulate a recursive rule that generates the sequence. This might involve experimenting with different combinations of previous terms and arithmetic or other operations. Finding a recursive rule would provide a definitive mathematical explanation for the sequence.
Advanced Analysis: Statistical and Probabilistic Approaches
If the sequence remains enigmatic after investigating basic mathematical relationships, we can turn to more advanced techniques:
1. Statistical Analysis:
Statistical analysis can help us determine if the sequence exhibits characteristics of randomness or if it displays a hidden structure. Techniques like autocorrelation and spectral analysis can reveal hidden periodicities or correlations within the data.
2. Information Theory:
Information theory can quantify the amount of information contained within the sequence. This can help us assess the complexity of the sequence and guide further analysis. A low information content might suggest randomness, while a high information content could indicate a structured pattern.
3. Probabilistic Modeling:
Probabilistic modeling can help us predict the next term in the sequence or the likelihood of observing certain patterns. Different models can be tested to find the best fit for the data. This approach is particularly useful if we suspect that the sequence is generated by a stochastic process (a process that involves random variables).
The Importance of Context and Further Investigation
The key to unlocking the mystery of "4 1 2 5 1 2" lies in understanding its origin and context. The sequence, without additional information, remains open to multiple interpretations. To gain a deeper understanding, we need answers to critical questions:
- Source: Where did this sequence originate? Knowing the source might provide crucial clues about its meaning.
- Purpose: What was the purpose of creating this sequence? Was it a code, a measurement, a puzzle, or simply a random set of numbers?
- Surrounding Data: Are there other related sequences or data points that could provide context?
Further investigation could involve seeking more information about its origin, looking for patterns in larger datasets containing the sequence, or applying more advanced statistical techniques. The challenge lies in defining a clear hypothesis for the sequence's generation and testing it rigorously.
Frequently Asked Questions (FAQ)
Q: Is the sequence "4 1 2 5 1 2" part of a known mathematical sequence?
A: Based on currently available information, it doesn't directly correspond to any widely known mathematical sequence like Fibonacci or arithmetic progressions. However, it could be a variation or a fragment of a larger, undiscovered sequence.
Q: Could this sequence be a code?
A: Yes, it's entirely possible. Without a key or further context, determining its meaning as a code is challenging. It could represent letters, symbols, or other data using a substitution or more complex cipher.
Q: What are some ways to analyze this sequence further?
A: Further analysis could involve statistical methods like autocorrelation, spectral analysis, or the application of information theory concepts to quantify its information content. Exploring recursive relationships and modular arithmetic are also viable approaches.
Q: Is the sequence random?
A: It's possible. Without a known origin or context, the assumption of randomness is as valid as any other interpretation until further evidence suggests otherwise. Statistical tests can help evaluate this hypothesis.
Conclusion: The Enduring Mystery and the Joy of Discovery
The sequence "4 1 2 5 1 2" presents a captivating challenge, reminding us that even seemingly simple numerical patterns can hold surprising depth and complexity. While this article has explored various interpretations and analytical approaches, the ultimate meaning remains elusive without additional context. The journey of decoding this sequence underscores the importance of observation, critical thinking, and the power of diverse analytical methods in unraveling mathematical and logical puzzles. The mystery surrounding this sequence highlights the enduring appeal of pattern recognition and the rewarding experience of mathematical discovery. It serves as a reminder that the quest for understanding is an ongoing process, and even seemingly simple patterns can lead us down fascinating paths of exploration. The true value of this exploration is not necessarily finding a definitive answer, but rather the process of critical thinking and problem-solving that it encourages.
Latest Posts
Latest Posts
-
How To Find Area Of A Parabola
Sep 22, 2025
-
What Expression Is Equivalent To Mc012 1 Jpg
Sep 22, 2025
-
How To Find Secant Line Equation
Sep 22, 2025
-
What Macromolecule Makes Up The Majority Of The Cell Membrane
Sep 22, 2025
-
What Is 5 3 As A Percent
Sep 22, 2025
Related Post
Thank you for visiting our website which covers about 4 1 2 5 1 2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.