3/4 + 1/2 Answer In Fraction
faraar
Sep 11, 2025 · 6 min read
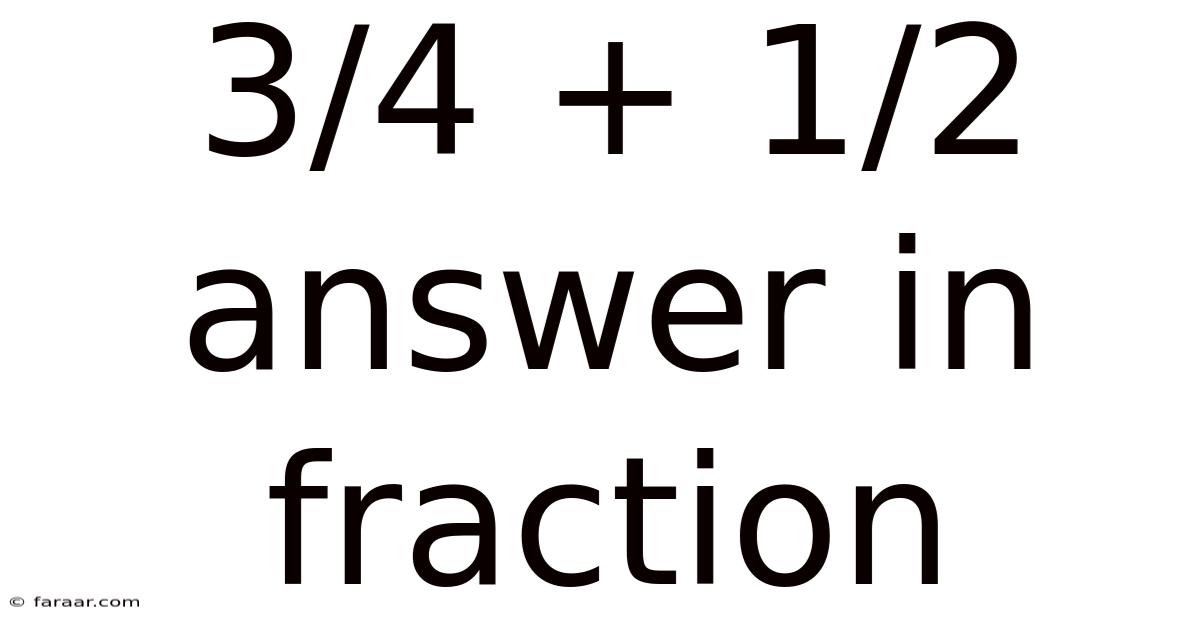
Table of Contents
Mastering Fractions: A Comprehensive Guide to Adding 3/4 and 1/2
Adding fractions might seem daunting at first, but with a little practice and understanding of the underlying principles, it becomes a straightforward process. This comprehensive guide will walk you through adding 3/4 and 1/2, explaining the steps in detail, exploring the underlying mathematical concepts, and answering frequently asked questions. Understanding this seemingly simple addition forms the foundation for more complex fractional arithmetic and is crucial for various applications in mathematics and beyond. This guide aims to demystify this process and build your confidence in working with fractions.
Understanding Fractions: A Quick Recap
Before diving into the addition, let's refresh our understanding of fractions. A fraction represents a part of a whole. It's composed of two key parts:
- Numerator: The top number, indicating how many parts we have.
- Denominator: The bottom number, indicating the total number of equal parts the whole is divided into.
For example, in the fraction 3/4, 3 is the numerator and 4 is the denominator. This means we have 3 out of 4 equal parts.
Adding Fractions: The Common Denominator
The fundamental rule of adding fractions is that they must have a common denominator. This means the bottom numbers (denominators) must be the same. If the denominators are different, we need to find a common denominator before we can add them.
This is where finding the least common multiple (LCM) comes in handy. The LCM is the smallest number that is a multiple of both denominators. Let's illustrate this with our example: 3/4 + 1/2.
Finding the Least Common Multiple (LCM)
Our denominators are 4 and 2. Let's find their LCM:
- Multiples of 4: 4, 8, 12, 16...
- Multiples of 2: 2, 4, 6, 8, 10...
The smallest number that appears in both lists is 4. Therefore, the LCM of 4 and 2 is 4. This will be our common denominator.
Converting Fractions to a Common Denominator
Now that we have our common denominator (4), we need to convert both fractions so they have this denominator.
-
3/4: This fraction already has a denominator of 4, so it remains unchanged.
-
1/2: To convert this fraction to a denominator of 4, we need to multiply both the numerator and the denominator by 2: (1 x 2) / (2 x 2) = 2/4
Now both fractions have the same denominator: 3/4 and 2/4.
Adding the Fractions
With both fractions having a common denominator, adding them is simple: we add the numerators and keep the denominator the same.
3/4 + 2/4 = (3 + 2) / 4 = 5/4
Simplifying the Fraction (Improper Fractions and Mixed Numbers)
The result, 5/4, is an improper fraction because the numerator (5) is larger than the denominator (4). We can convert this to a mixed number, which combines a whole number and a fraction.
To do this, we divide the numerator (5) by the denominator (4):
5 ÷ 4 = 1 with a remainder of 1
This means 5/4 is equal to 1 whole and 1/4. Therefore, the simplified answer is 1 1/4.
Visual Representation
Let's visualize this addition. Imagine a pizza cut into four equal slices.
- 3/4 represents having three slices.
- 1/2 represents having two slices (since 1/2 is equivalent to 2/4).
Adding the slices together (3 + 2 = 5), we have five slices in total. Since the pizza has only four slices, we have one whole pizza and one extra slice. This visually represents our answer of 1 1/4.
Mathematical Explanation: The Process in Detail
The process we followed can be formally described using the following steps:
-
Identify the denominators: Determine the denominators of the fractions being added (in this case, 4 and 2).
-
Find the least common multiple (LCM): Calculate the LCM of the denominators. This is the smallest number divisible by both denominators. Several methods exist for finding the LCM, including listing multiples or using prime factorization.
-
Convert fractions to equivalent fractions with the common denominator: Multiply the numerator and denominator of each fraction by the appropriate value to obtain the common denominator.
-
Add the numerators: Once the fractions share a common denominator, add the numerators together. The denominator remains unchanged.
-
Simplify the result: If the resulting fraction is an improper fraction (numerator greater than denominator), convert it to a mixed number (whole number and a fraction) by dividing the numerator by the denominator. The quotient becomes the whole number part, and the remainder becomes the numerator of the fractional part, while the denominator remains the same.
Expanding on the Concept: Adding More Than Two Fractions
The principles discussed above extend to adding more than two fractions. The key remains finding the least common multiple of all denominators and then converting all fractions to have this common denominator before adding the numerators.
Frequently Asked Questions (FAQ)
Q1: What if the LCM is difficult to find?
A1: For larger numbers, prime factorization can be a helpful technique to find the LCM. Break down each denominator into its prime factors, and then take the highest power of each prime factor present in the factorizations. Multiply these highest powers together to get the LCM.
Q2: Can I add fractions with different denominators directly without finding a common denominator?
A2: No. The common denominator is essential. Adding the numerators directly without a common denominator would be mathematically incorrect and would not represent the correct portion of the whole.
Q3: Are there other ways to simplify fractions?
A3: Yes. Besides converting improper fractions to mixed numbers, you can also simplify proper fractions (where the numerator is smaller than the denominator) by finding the greatest common divisor (GCD) of the numerator and denominator and dividing both by the GCD.
Q4: What are some real-world applications of adding fractions?
A4: Adding fractions is crucial in many areas, including cooking (measuring ingredients), construction (measuring materials), sewing (measuring fabric), and various scientific and engineering calculations.
Conclusion
Adding fractions, while seemingly simple, involves a systematic process requiring a thorough understanding of fractions and the concept of the least common multiple. By mastering these concepts and following the steps outlined above, you can confidently tackle the addition of fractions, whether it's adding 3/4 and 1/2 or more complex fractional expressions. Remember, practice is key! The more you work with fractions, the more intuitive and comfortable this process will become. This skill forms a cornerstone for more advanced mathematical concepts, making its mastery a worthwhile endeavor.
Latest Posts
Latest Posts
-
List Four Different Ways In Which Scientists Can Manipulate Dna
Sep 11, 2025
-
Find Three Consecutive Odd Integers Whose Sum Is 117
Sep 11, 2025
-
A 1 2 B1 B2 H Solve For B2
Sep 11, 2025
-
The Starting Substances In A Chemical Reaction
Sep 11, 2025
-
3x 2y 12 Solve For Y
Sep 11, 2025
Related Post
Thank you for visiting our website which covers about 3/4 + 1/2 Answer In Fraction . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.