3x 2y 12 Solve For Y
faraar
Sep 11, 2025 · 5 min read
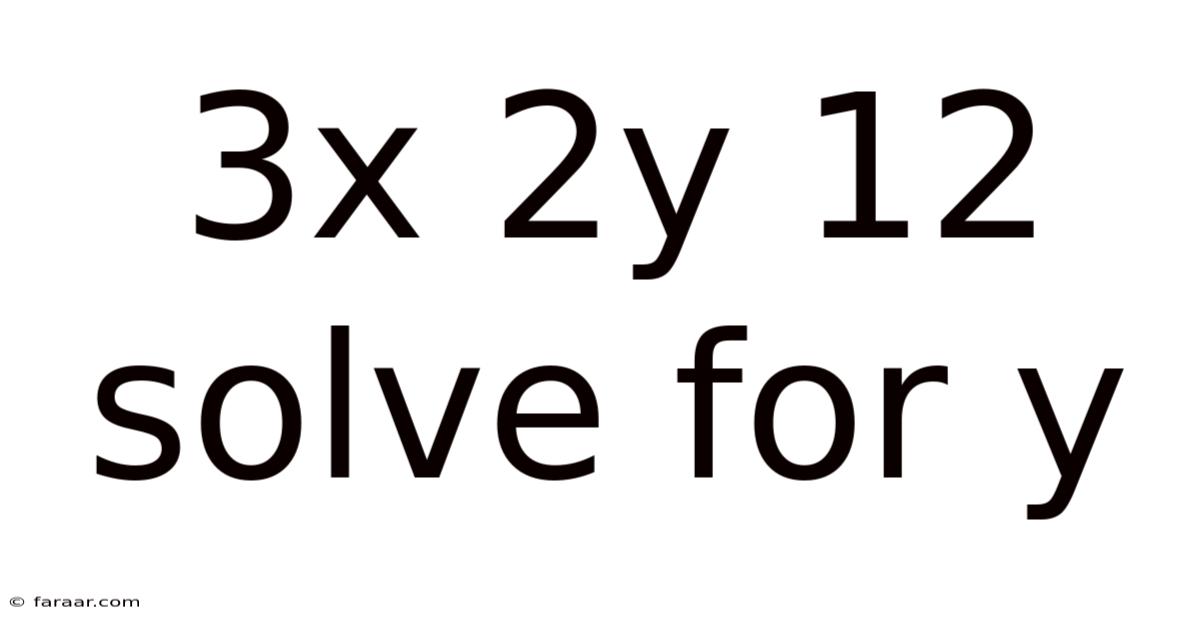
Table of Contents
Solving for y: A Deep Dive into 3x + 2y = 12
This article provides a comprehensive guide on how to solve the equation 3x + 2y = 12 for y. We'll explore the underlying algebraic principles, demonstrate the solution process step-by-step, and delve into various scenarios and applications. Understanding this seemingly simple equation unlocks a fundamental skill in algebra, crucial for tackling more complex problems in mathematics and related fields. This guide caters to students of all levels, from beginners needing a solid foundation to those seeking a deeper understanding of algebraic manipulation.
Introduction: Understanding Linear Equations
The equation 3x + 2y = 12 is a linear equation in two variables, x and y. A linear equation represents a straight line when graphed on a coordinate plane. The goal of "solving for y" is to isolate y on one side of the equation, expressing it as a function of x (y = f(x)). This allows us to easily determine the value of y for any given value of x. This process is fundamental to understanding linear relationships and their applications in various fields, including physics, economics, and computer science.
Step-by-Step Solution: Isolating y
Let's break down the process of solving 3x + 2y = 12 for y:
-
Identify the term containing y: In our equation, this is 2y.
-
Isolate the term containing y: To isolate 2y, we need to move the term 3x to the other side of the equation. We do this by subtracting 3x from both sides:
3x + 2y - 3x = 12 - 3x
This simplifies to:
2y = 12 - 3x
-
Solve for y: Now, we need to isolate y by dividing both sides of the equation by 2:
2y / 2 = (12 - 3x) / 2
This simplifies to:
y = (12 - 3x) / 2
-
Simplify (Optional): We can further simplify the expression by distributing the division:
y = 12/2 - (3x)/2
y = 6 - (3/2)x
or, equivalently:
y = 6 - 1.5x
Therefore, the solution for y in terms of x is y = 6 - (3/2)x or y = 6 - 1.5x. This equation tells us that for any given value of x, we can calculate the corresponding value of y.
Graphical Representation: Visualizing the Solution
The equation y = 6 - (3/2)x represents a straight line on a coordinate plane. The y-intercept (the point where the line crosses the y-axis) is 6, and the slope (the steepness of the line) is -3/2. This means the line slopes downwards from left to right. Plotting points using different values of x and calculating the corresponding y values using our equation will allow you to visually confirm the solution. For instance:
- If x = 0, y = 6 - (3/2)*0 = 6 (Point: (0, 6))
- If x = 2, y = 6 - (3/2)*2 = 3 (Point: (2, 3))
- If x = 4, y = 6 - (3/2)*4 = 0 (Point: (4, 0))
By plotting these points and drawing a line through them, you will obtain a visual representation of the solution to the equation 3x + 2y = 12.
Applications and Further Exploration
The ability to solve for a variable in a linear equation is essential in numerous applications:
-
Finding Intercepts: As shown above, we can easily find the x and y intercepts by setting y=0 and x=0 respectively and solving for the other variable. This is useful in graphing linear equations and understanding the equation's meaning in context.
-
Solving Systems of Equations: Solving for y (or x) is a crucial first step in solving systems of linear equations, which involve multiple equations with the same variables. Methods like substitution and elimination rely on isolating one variable in one equation before substituting it into another.
-
Modeling Real-World Problems: Linear equations are used to model a variety of real-world phenomena, from calculating distances and speeds to analyzing economic trends. Solving for a specific variable provides crucial insights into these models. For example, if 3x represents the cost of apples and 2y represents the cost of oranges, and 12 represents the total budget, solving for y would allow you to determine the maximum number of oranges you can buy given a specific number of apples.
-
Linear Programming: In operations research and management science, linear programming techniques are used to optimize resource allocation and decision-making under constraints. Solving linear equations is a fundamental part of this process.
Different Approaches: Alternative Methods
While the method described above is straightforward and commonly used, there are other ways to approach solving for y:
-
Using matrices: For more complex systems of equations, matrix methods can be more efficient. However, this method requires a deeper understanding of linear algebra.
-
Graphing Calculator: Graphing calculators can quickly solve for y or graphically represent the equation, allowing for visual confirmation of the solution.
Frequently Asked Questions (FAQ)
-
What if the equation is different? The basic principle remains the same. No matter the specific coefficients (the numbers in front of x and y), the steps involve isolating the term containing y and then solving for y by performing inverse operations.
-
What if there's a constant on the same side as 2y? First, move the constant to the other side of the equation by subtraction or addition before proceeding with the other steps.
-
What if the coefficient of y is negative? This simply means you'll divide both sides by a negative number, which will change the sign of the resulting expression.
-
Can I solve for x instead of y? Absolutely! The steps would be similar, but you would isolate the term containing x and then solve for x.
-
What does it mean if I end up with no solution or infinite solutions? These scenarios arise when dealing with inconsistent or dependent systems of equations, which go beyond the scope of a single equation like this.
Conclusion: Mastering the Fundamentals
Solving the equation 3x + 2y = 12 for y, resulting in y = 6 - (3/2)x, is more than just a mathematical exercise. It demonstrates a crucial algebraic skill applicable to a wide range of problems. Understanding the step-by-step process, visualizing the solution graphically, and exploring various applications significantly enhances your mathematical comprehension. This foundational knowledge empowers you to tackle more complex equations and real-world problems with confidence. Remember, practice is key to mastering this and other algebraic concepts. By working through various examples and applying the principles outlined here, you'll develop the fluency and understanding needed to succeed in mathematics and beyond.
Latest Posts
Latest Posts
-
Calculate Probability From Standard Deviation And Mean
Sep 11, 2025
-
The Product Of A Number And Negative 8
Sep 11, 2025
-
Swimming Lessons In Valley Stream Ny
Sep 11, 2025
-
Does A Rhombus Have 4 Congruent Angles
Sep 11, 2025
-
High School Math Tutors Near Me
Sep 11, 2025
Related Post
Thank you for visiting our website which covers about 3x 2y 12 Solve For Y . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.