A 1 2 B1 B2 H Solve For B2
faraar
Sep 11, 2025 · 6 min read
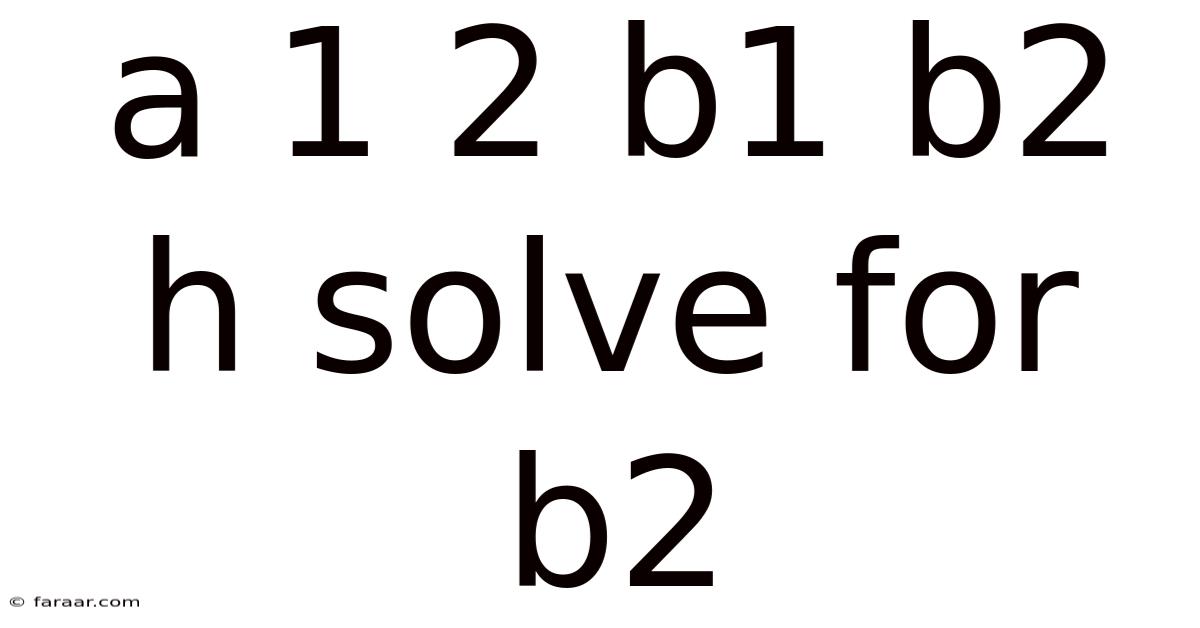
Table of Contents
Solving for b2: A Comprehensive Guide to Understanding and Applying the Formula
This article provides a comprehensive guide to solving for b2 in various mathematical contexts, primarily focusing on the quadratic formula and its applications in different fields. We will delve into the algebraic manipulation required, provide step-by-step examples, explore related concepts, and address frequently asked questions. Understanding how to solve for b2 is a fundamental skill in algebra and has wide-ranging applications in physics, engineering, finance, and more. This guide aims to make this seemingly complex task accessible to everyone, regardless of their prior mathematical background.
Introduction: Understanding the Context of "a 1 2 b1 b2 h"
The expression "a 1 2 b1 b2 h" likely refers to elements within a broader mathematical formula, most commonly found in the context of geometry or physics. Without further context, it is difficult to definitively state the exact formula. However, we can assume that the variables represent different parameters within a specific equation. Let's explore two common scenarios where similar expressions might appear:
-
Area of a Trapezoid: The area of a trapezoid is given by the formula: Area = ½(b1 + b2)h, where b1 and b2 are the lengths of the parallel sides (bases) and h is the height of the trapezoid. In this case, solving for b2 involves algebraic manipulation of this equation.
-
Equations of Motion (Physics): While less directly related to the given expression, equations of motion in physics often involve quadratic expressions. For instance, considering uniformly accelerated motion, we might encounter equations like s = ut + ½at², where s is the displacement, u is the initial velocity, a is the acceleration, and t is the time. Although this doesn't directly contain b1 or b2, understanding quadratic equations and their solutions is crucial for tackling more complex physics problems where such variables might emerge.
This article will primarily focus on solving for b2 within the context of the trapezoid area formula, as it directly incorporates the variables provided. However, the underlying algebraic principles apply equally to other scenarios involving quadratic or linear equations.
1. Solving for b2 in the Trapezoid Area Formula
The formula for the area of a trapezoid is:
Area = ½(b1 + b2)h
To solve for b2, we need to isolate it on one side of the equation. Let's follow these steps:
-
Step 1: Multiply both sides by 2: This eliminates the fraction. 2 * Area = (b1 + b2)h
-
Step 2: Divide both sides by h: This isolates the parenthesis containing b2. (2 * Area) / h = b1 + b2
-
Step 3: Subtract b1 from both sides: This finally isolates b2. (2 * Area) / h - b1 = b2
Therefore, the solution for b2 is:
b2 = (2 * Area) / h - b1
Example:
Let's say the area of a trapezoid is 30 square units, the length of one base (b1) is 4 units, and the height (h) is 5 units. We can find the length of the other base (b2) using the formula we derived:
b2 = (2 * 30) / 5 - 4 b2 = 60 / 5 - 4 b2 = 12 - 4 b2 = 8 units
2. Understanding the Underlying Algebraic Principles
The solution for b2 involves several fundamental algebraic principles:
-
Order of Operations (PEMDAS/BODMAS): Remember to follow the order of operations (Parentheses/Brackets, Exponents/Orders, Multiplication and Division, Addition and Subtraction) when manipulating equations.
-
Distributive Property: The distributive property states that a(b + c) = ab + ac. While not explicitly used in this specific example, it’s crucial in manipulating more complex equations involving parentheses.
-
Inverse Operations: To isolate a variable, we use inverse operations. For example, the inverse of addition is subtraction, and the inverse of multiplication is division.
3. Applications Beyond Geometry: Quadratic Equations and the Quadratic Formula
While the trapezoid example provides a direct application, solving for variables within quadratic equations often requires a more advanced approach. The general form of a quadratic equation is:
ax² + bx + c = 0
While this doesn't directly include b1 and b2, the principles remain the same: manipulate the equation to isolate the desired variable. Solving for x in this case often involves using the quadratic formula:
x = [-b ± √(b² - 4ac)] / 2a
Although we are not directly solving for a variable named b2 here, the concept of isolating a variable within a more complex equation mirrors the steps we took in the trapezoid example. Understanding quadratic equations and the quadratic formula is fundamental to solving many real-world problems in various fields.
4. Real-World Applications
The ability to solve for variables in equations like the trapezoid area formula and quadratic equations has numerous real-world applications:
-
Engineering: Calculating structural loads, designing bridges, and analyzing stress and strain in materials.
-
Physics: Determining projectile motion, calculating energy, and modeling gravitational forces.
-
Finance: Calculating compound interest, analyzing investment returns, and modeling financial growth.
-
Computer Science: Developing algorithms, modeling data structures, and solving optimization problems.
5. Frequently Asked Questions (FAQs)
-
Q: What if the height (h) of the trapezoid is zero? A: If h is zero, the trapezoid collapses into a line segment, and the area becomes zero. The formula becomes undefined because division by zero is not allowed.
-
Q: Can I solve for other variables in the trapezoid area formula? A: Yes, you can solve for b1 or h using similar algebraic manipulation techniques. Isolate the desired variable using inverse operations.
-
Q: What if the equation is more complex and involves multiple variables? A: For more complex equations, you may need to employ more advanced algebraic techniques such as substitution, elimination, or matrix methods to isolate the desired variable.
-
Q: Are there any online tools to help solve for b2? A: While several online calculators can solve for variables in equations, understanding the underlying process of algebraic manipulation is crucial for true comprehension and problem-solving ability. Using calculators solely without understanding the process defeats the purpose of learning.
-
Q: How can I improve my understanding of algebra? A: Practice is key! Work through various problems, explore different types of equations, and consult textbooks or online resources for explanations and examples.
6. Conclusion: Mastering the Fundamentals of Algebraic Manipulation
Solving for b2 in the trapezoid area formula, or any other variable in a given equation, is a foundational skill in mathematics and its applications. By understanding the fundamental algebraic principles—such as the order of operations, inverse operations, and the distributive property—you can confidently tackle a wide range of mathematical problems. This skill is not merely an academic exercise; it's a crucial tool for solving real-world problems across various disciplines, empowering you to analyze data, model systems, and make informed decisions. Continuous practice and a firm grasp of the underlying principles are essential for mastering algebraic manipulation and unlocking its immense potential. Remember, even seemingly complex problems can be broken down into manageable steps, leading you to a successful solution. The journey to mastering algebra is a rewarding one, and the ability to solve for any variable, including b2, is a testament to your growing mathematical prowess.
Latest Posts
Latest Posts
-
Calculate Probability From Standard Deviation And Mean
Sep 11, 2025
-
The Product Of A Number And Negative 8
Sep 11, 2025
-
Swimming Lessons In Valley Stream Ny
Sep 11, 2025
-
Does A Rhombus Have 4 Congruent Angles
Sep 11, 2025
-
High School Math Tutors Near Me
Sep 11, 2025
Related Post
Thank you for visiting our website which covers about A 1 2 B1 B2 H Solve For B2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.