10 To The Power Of -11
faraar
Sep 17, 2025 · 5 min read
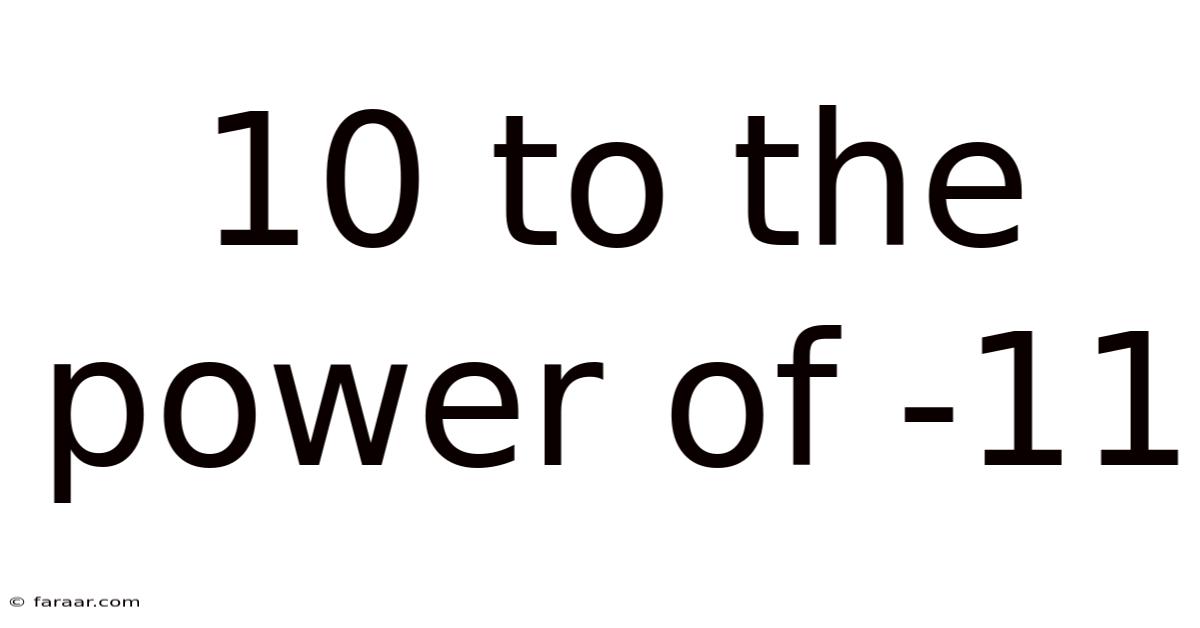
Table of Contents
Unraveling the Mystery of 10 to the Power of -11: A Deep Dive into Scientific Notation
10 to the power of -11, or 10⁻¹¹, is a seemingly small number, but it represents a significant concept in science and mathematics. Understanding this notation is crucial for comprehending vast scales in the universe, from the microscopic world of atoms to the immense expanse of space. This article will explore 10⁻¹¹ in detail, explaining its meaning, applications, and significance across various scientific disciplines. We'll unpack its implications and demonstrate how this seemingly insignificant number plays a vital role in our understanding of the world around us.
Understanding Scientific Notation and Negative Exponents
Before delving into the specifics of 10⁻¹¹, let's establish a firm grasp on scientific notation. Scientific notation is a way of expressing very large or very small numbers concisely. It uses powers of 10 to represent the magnitude of the number. A number written in scientific notation takes the form a x 10<sup>b</sup>, where 'a' is a number between 1 and 10 (but not including 10), and 'b' is an integer representing the power of 10.
Negative exponents in scientific notation indicate that the number is smaller than 1. Each negative power of 10 moves the decimal point one place to the left. For example:
- 10⁻¹ = 0.1
- 10⁻² = 0.01
- 10⁻³ = 0.001
Following this pattern, 10⁻¹¹ represents a number with the decimal point moved eleven places to the left of 1. Therefore, 10⁻¹¹ is equal to 0.00000000001.
Visualizing 10⁻¹¹: Bringing Abstract Concepts to Life
It's difficult to truly grasp the scale of 10⁻¹¹ without some visual aids. Imagine a meter stick. A centimeter is one-hundredth of a meter (10⁻² meters). A millimeter is one-thousandth of a meter (10⁻³ meters). Now, try to visualize something a thousand times smaller than a millimeter – that’s approaching the scale of 10⁻¹¹.
To put it into perspective, consider these examples:
-
Nanotechnology: The realm of nanotechnology deals with structures at the nanoscale, typically ranging from 1 to 100 nanometers. One nanometer is 10⁻⁹ meters. Therefore, 10⁻¹¹ meters is even smaller than a nanometer, falling within the realm of picometers (10⁻¹² meters).
-
Atomic Dimensions: The diameter of an atom is on the order of 10⁻¹⁰ meters. 10⁻¹¹ meters is only a tenth of the diameter of an atom, a scale that pushes the boundaries of our current observational capabilities.
-
Subatomic Particles: We venture into the subatomic world when we consider distances at the scale of 10⁻¹¹, delving into the realm of quarks and other fundamental particles whose precise dimensions remain subject to ongoing scientific investigation.
Applications of 10⁻¹¹ in Science and Technology
Despite its tiny magnitude, 10⁻¹¹ meters and related scales have immense significance in various scientific fields:
-
Nuclear Physics: The size of atomic nuclei and the distances between nucleons (protons and neutrons) are on the order of 10⁻¹⁵ meters, making 10⁻¹¹ meters relevant when dealing with calculations related to nuclear forces and reactions. Understanding these minuscule distances is crucial in areas such as nuclear energy and nuclear medicine.
-
Quantum Mechanics: Quantum mechanics deals with phenomena at the atomic and subatomic levels, where 10⁻¹¹ meters represents a significant length scale. Quantum effects become increasingly important at this scale, impacting the behavior of matter and energy.
-
High-Precision Measurement: Advancements in metrology enable the measurement of incredibly small distances. Techniques like atomic force microscopy (AFM) and scanning tunneling microscopy (STM) allow scientists to probe the surface topography of materials at resolutions approaching or exceeding 10⁻¹¹ meters, enabling the development of novel materials and devices.
-
Material Science: The properties of materials are profoundly influenced by their atomic structure and bonding. Understanding the interactions between atoms and molecules at 10⁻¹¹ meter scales is crucial for designing materials with specific properties, such as high strength, conductivity, or reactivity. This contributes to developments in numerous fields, from aerospace engineering to medicine.
-
Astrophysics: While seemingly counterintuitive, 10⁻¹¹ plays a role even in astrophysics. When dealing with vast distances in space, the relative differences between extremely large numbers might be expressed using such small values to define precision or deviations in astronomical measurements.
10⁻¹¹ and the Limits of Measurement: Pushing the Boundaries of Observation
Measuring something as small as 10⁻¹¹ meters presents significant technological challenges. Current measurement techniques are constantly being refined to reach ever-higher levels of precision. This continuous drive for improved measurement capabilities is crucial for advancing our understanding of the fundamental laws of physics and the nature of matter. The development of new tools and techniques is essential to explore the world at this minuscule scale.
Frequently Asked Questions (FAQs)
Q: How do I convert 10⁻¹¹ meters to other units?
A: To convert 10⁻¹¹ meters to other units, use appropriate conversion factors. For example:
- To convert to nanometers (nm): 10⁻¹¹ m * (10⁹ nm/1 m) = 10⁻² nm = 0.01 nm
- To convert to picometers (pm): 10⁻¹¹ m * (10¹² pm/1 m) = 10 pm
Q: What is the significance of using scientific notation?
A: Scientific notation is essential for representing extremely large or small numbers concisely and efficiently. It simplifies calculations and facilitates comparisons between numbers of vastly different magnitudes.
Q: Are there any practical applications of working with numbers as small as 10⁻¹¹?
A: While not directly used in everyday life, understanding and working with numbers at this scale is crucial for advancements in fields like nanotechnology, material science, and quantum mechanics, leading to innovations in various technologies and industries.
Q: What are some examples of physical quantities that might be measured in units related to 10⁻¹¹ meters?
A: Examples include the wavelength of certain types of electromagnetic radiation, the distance between atoms in a crystal lattice, and the size of certain subatomic particles.
Conclusion: The Significance of the Small
While 10⁻¹¹ might appear insignificant at first glance, its true importance lies in its ability to represent and quantify the extraordinarily small scales relevant to fundamental aspects of our universe. Understanding this notation and its implications is crucial for appreciating the intricate workings of the universe, from the fundamental forces that govern the behavior of matter to the incredible precision required for advanced technological achievements. As we continue to push the boundaries of scientific discovery, the significance of 10⁻¹¹ and similar scales will only continue to grow, driving advancements in various scientific and technological fields. The exploration of the infinitely small continues to unveil profound insights into the fabric of reality.
Latest Posts
Latest Posts
-
Consecutive Angles Of A Parallelogram Are Supplementary
Sep 17, 2025
-
What Is The Gcf Of 42 And 14
Sep 17, 2025
-
Find Four Consecutive Integers With The Sum Of 54
Sep 17, 2025
-
Eliminate The Parameter T To Find A Cartesian Equation For
Sep 17, 2025
-
Match Each Task With Its Corresponding Memory Type
Sep 17, 2025
Related Post
Thank you for visiting our website which covers about 10 To The Power Of -11 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.