What Is The Gcf Of 42 And 14
faraar
Sep 17, 2025 · 5 min read
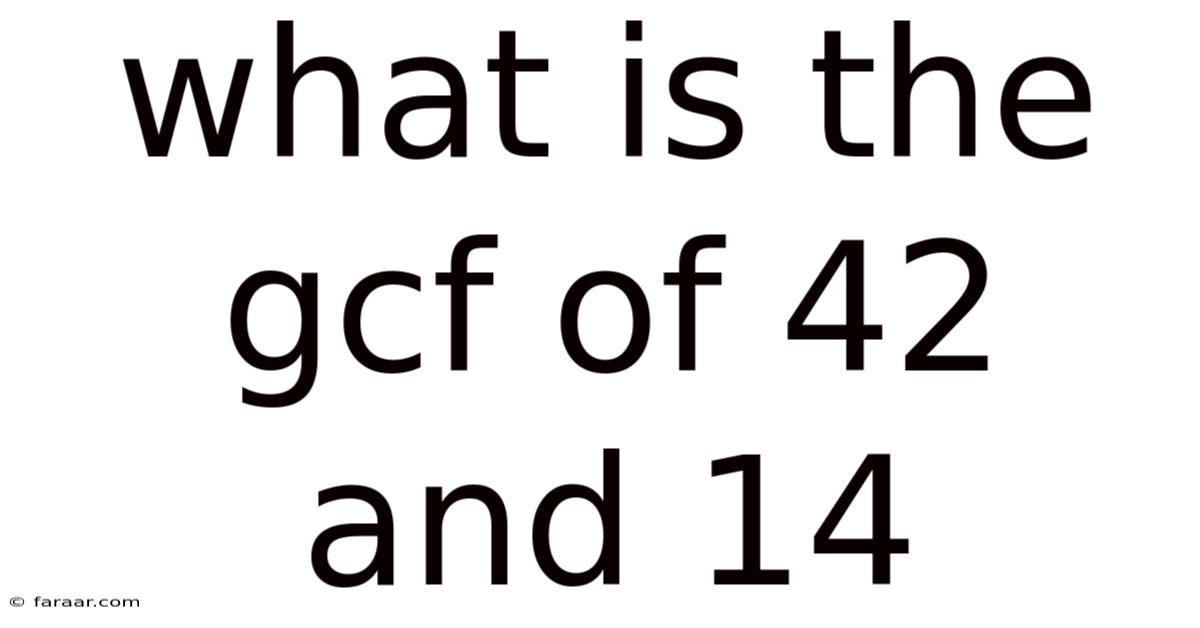
Table of Contents
Unveiling the Greatest Common Factor (GCF) of 42 and 14: A Deep Dive into Number Theory
Finding the greatest common factor (GCF), also known as the greatest common divisor (GCD), of two numbers might seem like a simple arithmetic task. However, understanding the underlying principles reveals a fascinating glimpse into number theory and its applications in various fields, from cryptography to computer science. This article will not only determine the GCF of 42 and 14 but will also explore different methods for calculating the GCF, delving into the theoretical underpinnings and providing practical examples to solidify your understanding.
Introduction: What is the Greatest Common Factor (GCF)?
The greatest common factor (GCF) of two or more integers is the largest positive integer that divides each of the integers without leaving a remainder. In simpler terms, it's the biggest number that goes evenly into both numbers. For example, the GCF of 12 and 18 is 6 because 6 is the largest number that divides both 12 and 18 without leaving a remainder. Understanding the GCF is crucial in simplifying fractions, solving algebraic equations, and understanding more complex mathematical concepts. This article will focus on determining the GCF of 42 and 14, employing multiple methods to illustrate the versatility of this fundamental concept.
Method 1: Prime Factorization
This method is arguably the most fundamental and conceptually clear way to find the GCF. It involves breaking down each number into its prime factors—numbers that are only divisible by 1 and themselves.
- Step 1: Find the prime factorization of 42.
We can express 42 as a product of its prime factors: 2 x 3 x 7.
- Step 2: Find the prime factorization of 14.
The prime factorization of 14 is 2 x 7.
- Step 3: Identify common prime factors.
Both 42 and 14 share the prime factors 2 and 7.
- Step 4: Multiply the common prime factors.
Multiplying the common prime factors together gives us 2 x 7 = 14.
Therefore, the GCF of 42 and 14 is 14.
Method 2: Listing Factors
This method involves listing all the factors of each number and then identifying the largest common factor. While straightforward for smaller numbers, this method becomes cumbersome for larger numbers.
- Step 1: List the factors of 42.
The factors of 42 are 1, 2, 3, 6, 7, 14, 21, and 42.
- Step 2: List the factors of 14.
The factors of 14 are 1, 2, 7, and 14.
- Step 3: Identify common factors.
The common factors of 42 and 14 are 1, 2, 7, and 14.
- Step 4: Determine the greatest common factor.
The greatest among the common factors is 14.
Therefore, the GCF of 42 and 14 is 14.
Method 3: Euclidean Algorithm
The Euclidean algorithm is a highly efficient method for finding the GCF of two integers, especially useful when dealing with larger numbers. It's based on the principle that the GCF of two numbers doesn't change if the larger number is replaced by its difference with the smaller number. This process is repeated until the two numbers are equal, and that number is the GCF.
- Step 1: Divide the larger number (42) by the smaller number (14).
42 ÷ 14 = 3 with a remainder of 0.
- Step 2: Interpret the result.
Since the remainder is 0, the smaller number (14) is the GCF.
Therefore, the GCF of 42 and 14 is 14.
Understanding the Significance of the GCF
The GCF has numerous applications across various mathematical domains and practical scenarios:
-
Simplifying Fractions: The GCF is essential for reducing fractions to their simplest form. For instance, the fraction 42/14 can be simplified to 3/1 (or simply 3) by dividing both the numerator and the denominator by their GCF, which is 14.
-
Solving Equations: The GCF plays a crucial role in solving certain types of algebraic equations, particularly those involving factoring and simplifying expressions.
-
Number Theory: The GCF is a fundamental concept in number theory, forming the basis for more advanced theorems and concepts like the least common multiple (LCM).
-
Cryptography: GCF calculations are integral to various cryptographic algorithms, ensuring secure data transmission and storage.
-
Computer Science: The GCF, particularly the Euclidean algorithm, is used in various computer science applications, such as simplifying calculations and optimizing algorithms.
Why is 14 the GCF of 42 and 14? A Deeper Look
The fact that 14 is the GCF of 42 and 14 is inherently linked to the divisibility rules and the prime factorization of both numbers. 42 is a multiple of 14 (42 = 14 x 3), meaning 14 divides 42 evenly. Since 14 divides itself evenly (14 = 14 x 1), and there's no larger number that divides both 42 and 14 without leaving a remainder, 14 is unequivocally the greatest common factor. This underscores the relationship between divisibility, factors, and the concept of the GCF.
Frequently Asked Questions (FAQs)
-
What is the difference between GCF and LCM? The greatest common factor (GCF) is the largest number that divides two or more numbers without leaving a remainder. The least common multiple (LCM) is the smallest number that is a multiple of two or more numbers.
-
Can the GCF of two numbers be 1? Yes, if two numbers have no common factors other than 1, their GCF is 1. Such numbers are called relatively prime or coprime.
-
Is there a limit to the size of numbers for which the GCF can be calculated? No, the methods described (especially the Euclidean algorithm) can be used to calculate the GCF of arbitrarily large numbers.
-
Why is the Euclidean algorithm efficient? The Euclidean algorithm is efficient because it reduces the size of the numbers involved in each step, converging quickly to the GCF, even for large numbers.
Conclusion: Mastering the GCF
Finding the greatest common factor of two numbers, as demonstrated with 42 and 14, is a fundamental skill in mathematics. Understanding the different methods—prime factorization, listing factors, and the Euclidean algorithm—allows for flexibility in approaching such problems. This knowledge extends beyond simple arithmetic, serving as a building block for more advanced mathematical concepts and real-world applications. Mastering the GCF isn’t merely about finding a number; it’s about understanding the deeper relationships within number theory and its practical relevance in various fields. The GCF, a seemingly simple concept, reveals a surprisingly rich and intricate world of mathematical possibilities.
Latest Posts
Latest Posts
-
A Number Is At Least 16
Sep 17, 2025
-
When I Was 6 My Sister Answer
Sep 17, 2025
-
How To Find The Standard Matrix Of A Linear Transformation
Sep 17, 2025
-
How To Find The Points Of Discontinuity
Sep 17, 2025
-
What Are The Vertices Of Pqr
Sep 17, 2025
Related Post
Thank you for visiting our website which covers about What Is The Gcf Of 42 And 14 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.