Find Four Consecutive Integers With The Sum Of 54.
faraar
Sep 17, 2025 · 5 min read
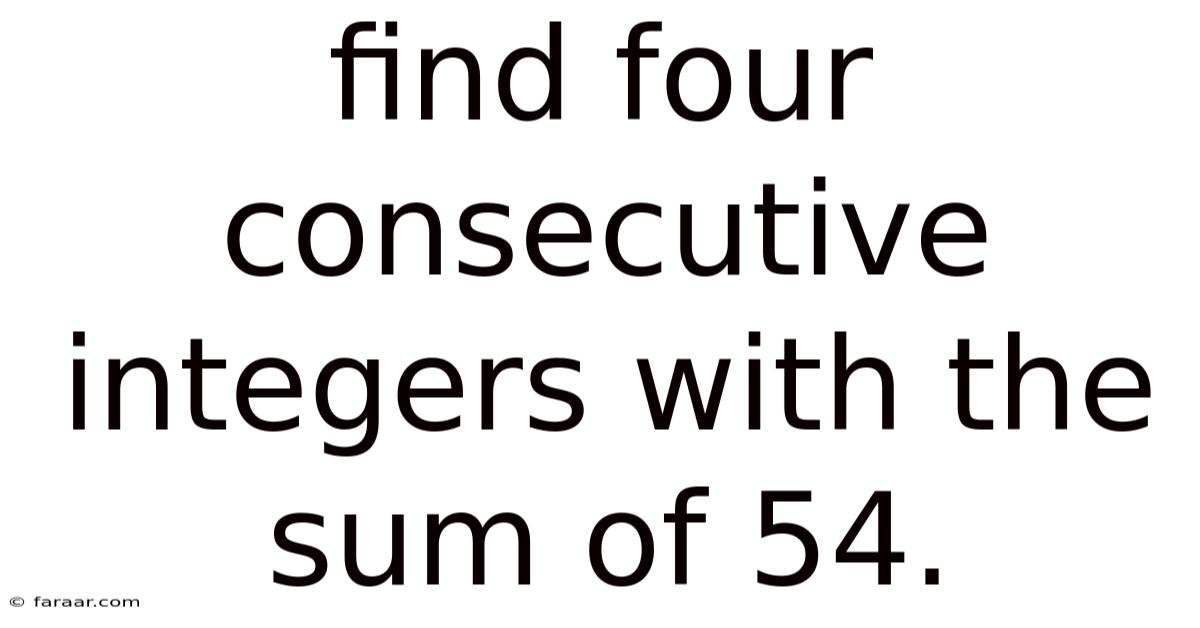
Table of Contents
Finding Four Consecutive Integers that Sum to 54: A Deep Dive into Problem Solving
This article explores the problem of finding four consecutive integers whose sum is 54. We'll move beyond simply finding the answer to understand the underlying mathematical principles, explore different solution methods, and delve into the broader context of solving similar problems. This will equip you with the skills to tackle a wide range of arithmetic and algebraic problems.
Introduction: Understanding the Problem
The core of the problem lies in translating a word problem into a mathematical equation. We're looking for four numbers that follow each other sequentially (consecutive integers) and add up to 54. This seemingly simple problem offers a great opportunity to practice fundamental algebraic techniques and develop problem-solving strategies. We'll examine both arithmetic and algebraic approaches, highlighting their strengths and weaknesses.
Method 1: The Arithmetic Approach - Trial and Error
While not the most elegant method, a trial-and-error approach can be surprisingly effective, especially for smaller numbers. We can start by estimating. If we divide 54 by 4, we get 13.5. This suggests that our integers will be centered around 13.5. Let's try a few sets:
- 11 + 12 + 13 + 14 = 50 (Too low)
- 12 + 13 + 14 + 15 = 54 (Correct!)
This method works well for simple problems but becomes inefficient and impractical for larger numbers or more complex scenarios.
Method 2: The Algebraic Approach - Using Variables
This method is more powerful and generalizable. We can represent the four consecutive integers using variables. Let's say:
- The first integer is x
- The second integer is x + 1
- The third integer is x + 2
- The fourth integer is x + 3
Now, we can write an equation representing the sum:
x + (x + 1) + (x + 2) + (x + 3) = 54
Simplifying the equation:
4x + 6 = 54
Subtracting 6 from both sides:
4x = 48
Dividing both sides by 4:
x = 12
Therefore, the first integer is 12. The four consecutive integers are:
- 12, 13, 14, and 15
Expanding the Problem: Generalizing the Solution
Let's generalize our algebraic solution. Suppose we want to find n consecutive integers that add up to a sum S. We can use the following formula:
x + (x + 1) + (x + 2) + ... + (x + n - 1) = S
This can be simplified to:
nx + (1 + 2 + ... + (n - 1)) = S
The sum of integers from 1 to (n - 1) can be calculated using the formula: (n - 1)n/2. Substituting this, we get:
nx + (n - 1)n/2 = S
This formula allows us to solve for x (the first integer) given any n (number of consecutive integers) and S (the sum). Let's use it to verify our original problem:
4x + (4 - 1)4/2 = 54 4x + 6 = 54 4x = 48 x = 12
Solving Similar Problems: Variations and Extensions
The core principles used to solve this problem can be applied to many similar situations. Consider these variations:
-
Finding consecutive even or odd integers: If we are dealing with consecutive even integers, we would represent them as x, x + 2, x + 4, x + 6. For consecutive odd integers, we would use x, x + 2, x + 4, x + 6. The methodology remains the same – set up an equation and solve for x.
-
Finding a different number of consecutive integers: The generalized formula we derived earlier can be used to find any number of consecutive integers adding up to a given sum. Simply substitute the values of n and S and solve for x.
-
Problems involving other arithmetic progressions: This problem is a specific case of finding the sum of an arithmetic sequence. The principles used here can be extended to other sequences with a common difference.
The Importance of Understanding the Underlying Mathematics
The seemingly simple problem of finding four consecutive integers that add up to 54 provides a powerful illustration of the importance of understanding the underlying mathematics. While trial and error can work for simple cases, the algebraic approach is far more robust, efficient, and generalizable. Developing the ability to translate word problems into mathematical equations is a crucial skill in mathematics and beyond. This ability allows you to tackle complex problems systematically and solve for unknowns.
Frequently Asked Questions (FAQ)
Q1: Can this problem be solved without algebra?
A1: Yes, a trial-and-error approach can work, especially for smaller numbers. However, it becomes increasingly inefficient for larger numbers or more complex variations.
Q2: What if the sum wasn't 54, but a different number?
A2: The algebraic method is easily adaptable. Simply substitute the new sum into the equation (4x + 6 = S) and solve for x.
Q3: Can this method be used for consecutive numbers that aren't integers?
A3: Yes, the algebraic approach is generalizable to consecutive numbers that are not integers (e.g., consecutive decimals). You'll use the same principles to build and solve your equation.
Q4: Are there any other ways to solve this problem?
A4: While less common for this specific problem, you could potentially use graphical methods or advanced mathematical concepts for similar problems in more complex scenarios.
Q5: What is the significance of this problem in higher-level mathematics?
A5: This problem introduces fundamental concepts of algebra, arithmetic sequences, and equation solving, all of which are building blocks for more advanced mathematical topics like calculus and number theory.
Conclusion: Beyond the Numbers
Solving the problem of finding four consecutive integers with a sum of 54 is more than just arriving at the answer (12, 13, 14, 15). It’s about mastering a problem-solving process, understanding the power of algebraic methods, and appreciating the underlying mathematical principles. The skills developed through this problem – translating word problems into equations, simplifying expressions, and solving for unknowns – are invaluable tools for tackling more complex mathematical challenges in the future. This problem serves as a stepping stone to a deeper understanding of mathematics and the beauty of its applications. It encourages a mindset of exploring different approaches, verifying solutions, and generalizing the solution process to solve a broader range of problems. This problem-solving approach isn't just confined to mathematics; it is a valuable skill applicable to various aspects of life, promoting critical thinking and analytical skills.
Latest Posts
Latest Posts
-
A Number Is At Least 16
Sep 17, 2025
-
When I Was 6 My Sister Answer
Sep 17, 2025
-
How To Find The Standard Matrix Of A Linear Transformation
Sep 17, 2025
-
How To Find The Points Of Discontinuity
Sep 17, 2025
-
What Are The Vertices Of Pqr
Sep 17, 2025
Related Post
Thank you for visiting our website which covers about Find Four Consecutive Integers With The Sum Of 54. . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.