X1 X2 2 Y1 Y2 2
faraar
Sep 16, 2025 · 7 min read
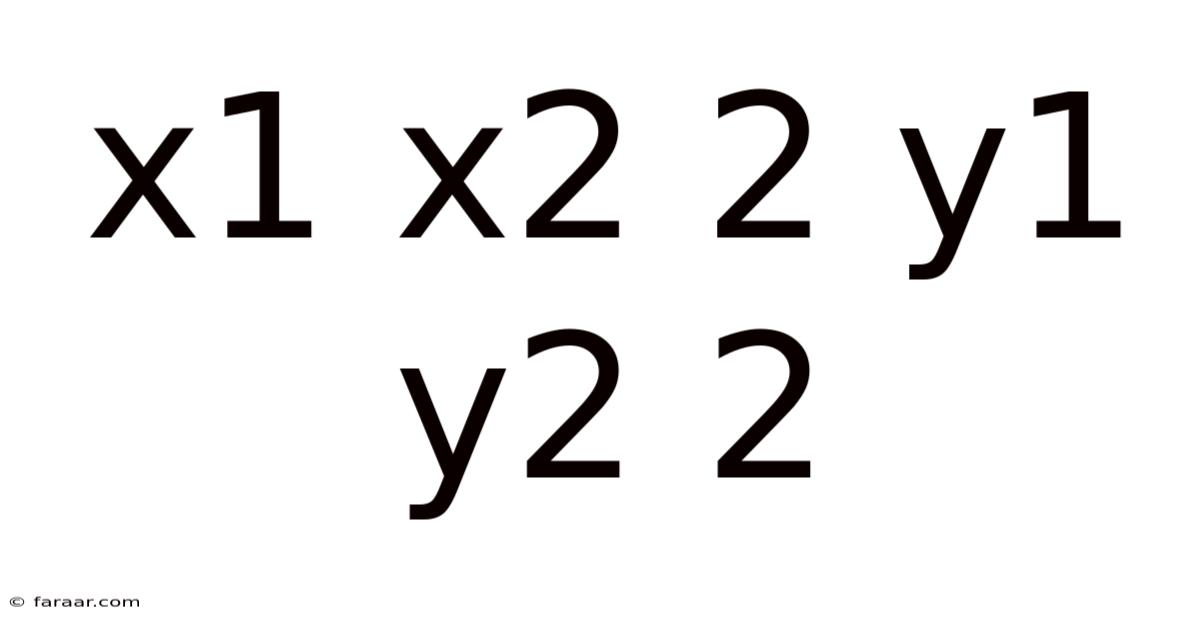
Table of Contents
Decoding the Mystery: A Deep Dive into x1 x2 2 y1 y2 2
The expression "x1 x2 2 y1 y2 2" might initially seem cryptic, like a secret code from a mathematical society. However, with a little unpacking, we can reveal its significance and understand its implications in various mathematical contexts. This seemingly simple expression opens doors to concepts like distance formulas, vector operations, and even the foundations of Euclidean geometry. This article will explore this expression in depth, examining its meaning, applications, and broader mathematical implications.
Understanding the Components: Variables and Operations
Before delving into the intricacies, let's dissect the expression itself. We have four variables: x1, x2, y1, and y2. These variables typically represent coordinates in a two-dimensional space. Think of them as points on a graph, where x represents the horizontal position and y represents the vertical position. The subscripts "1" and "2" differentiate between two distinct points: Point 1 (x1, y1) and Point 2 (x2, y2).
The "2" following each variable pair suggests an operation of squaring. And, implicitly, the addition signs (+) between the squared terms indicate that we're summing these squared differences. Therefore, the whole expression represents a calculation involving the differences in the x-coordinates and the y-coordinates of two points.
The Distance Formula: Unveiling the Geometric Significance
The expression "x1 x2 2 y1 y2 2" is fundamentally related to the distance formula in two-dimensional Euclidean space. This formula calculates the straight-line distance between two points (x1, y1) and (x2, y2). The complete distance formula is:
d = √[(x2 - x1)² + (y2 - y1)²]
Notice the striking similarity? The expression "x1 x2 2 y1 y2 2" forms the core of the distance formula – specifically, the radicand (the expression inside the square root). This means that the value of "(x2 - x1)² + (y2 - y1)²" represents the square of the distance between the two points.
To clarify, let's walk through a simple example. Consider two points: Point 1 (2, 3) and Point 2 (5, 7). Let's calculate the square of the distance between them using our expression:
(5 - 2)² + (7 - 3)² = 3² + 4² = 9 + 16 = 25
Therefore, the square of the distance between these two points is 25. To find the actual distance, we take the square root: √25 = 5. The distance between Point 1 and Point 2 is 5 units.
Applications Beyond the Distance Formula: Vectors and More
While the connection to the distance formula is prominent, the expression’s applications extend far beyond simply calculating distances. It plays a crucial role in various mathematical operations, especially those involving vectors.
-
Vector Magnitude: In vector algebra, the expression (x2 - x1)² + (y2 - y1)² represents the squared magnitude (or squared length) of the vector connecting Point 1 to Point 2. The magnitude of a vector is its length and is frequently used in physics and engineering to represent quantities like displacement, velocity, or force.
-
Vector Dot Product: The dot product of two vectors is a scalar (a single number) that can be interpreted geometrically as the product of the magnitudes of the two vectors and the cosine of the angle between them. While not directly equal to our expression, components of this calculation are inherently linked. The squared magnitudes of individual vectors are calculated using similar principles.
-
Variance and Standard Deviation: In statistics, this expression finds application in calculating variance and standard deviation. If we consider the coordinates as data points, the calculation is closely related to the sum of squared differences from the mean, a fundamental concept in statistical analysis. In essence, you could think of x1 and x2 as individual data points and the operation as the squared difference of these values around a hypothetical mean.
Expanding the Dimensions: Moving Beyond Two Dimensions
While our discussion has focused on two dimensions (x and y), the core concept easily extends to higher dimensions. For three dimensions (x, y, z), the analogous expression for the square of the distance between points (x1, y1, z1) and (x2, y2, z2) becomes:
(x2 - x1)² + (y2 - y1)² + (z2 - z1)²
This pattern continues for even higher dimensions. Each added dimension simply adds another squared difference term to the sum. This extension highlights the fundamental nature of the expression – it's a representation of the squared Euclidean distance between two points in any number of dimensions.
A Deeper Dive: The Pythagorean Theorem and its Implications
At the heart of the expression "x1 x2 2 y1 y2 2" lies the Pythagorean Theorem. This theorem, fundamental to Euclidean geometry, states that in a right-angled triangle, the square of the hypotenuse (the longest side) is equal to the sum of the squares of the other two sides.
The expression mirrors this theorem. The difference in x-coordinates (x2 - x1) and the difference in y-coordinates (y2 - y1) represent the lengths of the two legs of a right-angled triangle. The expression then calculates the square of the hypotenuse, which is the direct distance between the two points. This highlights the deep connection between the seemingly simple algebraic expression and fundamental geometric principles.
Practical Applications and Real-World Examples
The concepts discussed here are not confined to theoretical mathematics. They have widespread practical applications in various fields:
-
Computer Graphics and Game Development: Calculating distances between points is crucial for rendering images, detecting collisions, and managing object interactions in video games and computer-generated imagery.
-
Navigation and GPS Systems: GPS technology relies heavily on distance calculations to determine locations, plot routes, and calculate travel times. The distance formula, rooted in our expression, is the underlying mathematical engine powering these systems.
-
Robotics and Automation: In robotics, precise distance calculations are essential for robot navigation, obstacle avoidance, and accurate manipulation of objects.
-
Physics and Engineering: Many physical quantities, such as displacement, velocity, and force, are represented as vectors. The magnitude of these vectors, calculated using principles directly related to our expression, is crucial in solving various engineering and physics problems.
-
Machine Learning and Data Science: Distance calculations are frequently used in machine learning algorithms, such as k-nearest neighbors, which rely on measuring the proximity of data points to classify or predict outcomes.
Frequently Asked Questions (FAQ)
Q1: What happens if x1 = x2 and y1 = y2?
A1: If x1 = x2 and y1 = y2, then the expression evaluates to 0. This makes intuitive sense, as the distance between a point and itself is zero.
Q2: Can this expression be used with negative coordinates?
A2: Yes, absolutely. The squaring operation ensures that negative differences are treated correctly and contribute positively to the overall squared distance.
Q3: What if I have more than two points? How do I calculate the total distance?
A3: Calculating the total distance between multiple points requires a different approach. You'd need to calculate the individual distances between consecutive points and then sum those distances.
Q4: Is there a simpler way to represent this concept without the explicit squaring?
A4: No, the squaring is essential because it allows us to correctly calculate the distance using the Pythagorean theorem. Without squaring, we wouldn't obtain the correct Euclidean distance.
Q5: Are there alternative distance metrics besides the Euclidean distance?
A5: Yes, while Euclidean distance is the most common, there are other distance metrics, such as Manhattan distance (also known as L1 distance), which calculates distance along axes rather than a direct line.
Conclusion
The seemingly simple expression "x1 x2 2 y1 y2 2" reveals a wealth of mathematical significance. From its fundamental connection to the distance formula and the Pythagorean theorem to its applications in vectors, statistics, and various fields of science and engineering, this expression is a cornerstone of numerous mathematical concepts. Understanding its implications provides a deeper appreciation of the elegant interconnectivity between algebra, geometry, and their practical applications in the real world. This foundational understanding paves the way for further exploration into more complex mathematical concepts and their diverse applications across various disciplines.
Latest Posts
Latest Posts
-
Can You Use The Word We In A Research Paper
Sep 16, 2025
-
Write The Quotient In The Form A Bi
Sep 16, 2025
-
How To Calculate Protein Concentration From Absorbance
Sep 16, 2025
-
Y Varies Directly As X And Inversely As Z
Sep 16, 2025
-
What Is The Total Area Of The Figure
Sep 16, 2025
Related Post
Thank you for visiting our website which covers about X1 X2 2 Y1 Y2 2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.