Y Varies Directly As X And Inversely As Z
faraar
Sep 16, 2025 · 6 min read
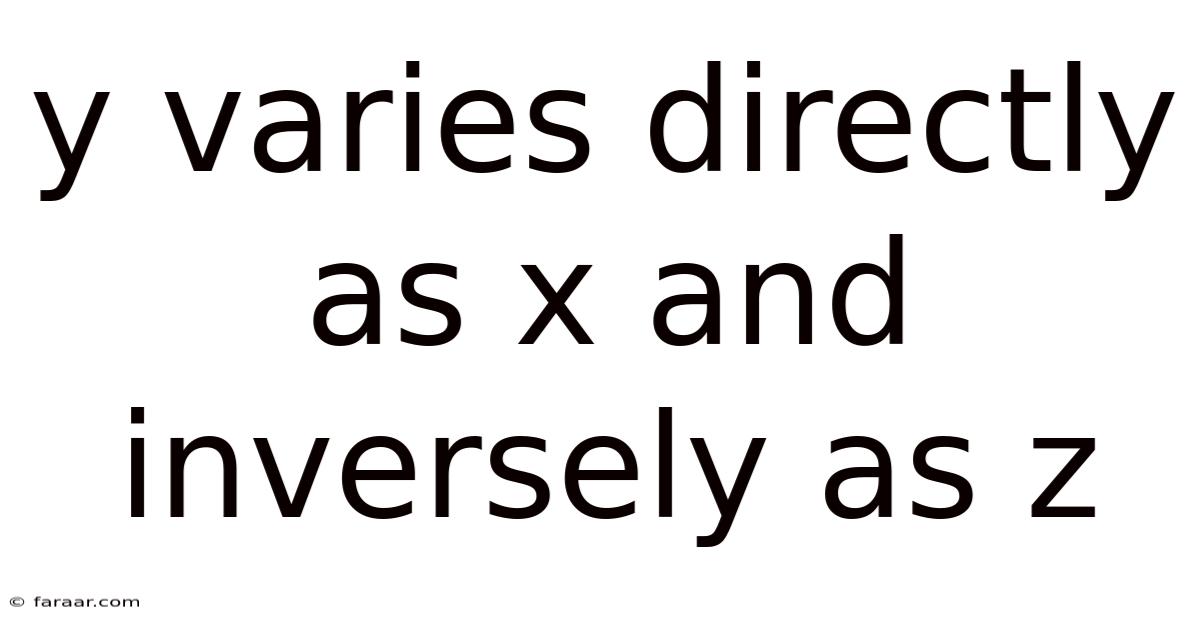
Table of Contents
Understanding Direct and Inverse Variation: When Y Varies Directly as X and Inversely as Z
This article delves into the concept of combined variation, specifically where one variable (y) varies directly with another (x) and inversely with a third (z). Understanding this relationship is crucial in various fields, from physics and engineering to economics and data analysis. We'll explore the underlying principles, demonstrate how to solve problems involving this type of variation, and clarify common misconceptions. This comprehensive guide will equip you with the tools to confidently tackle problems involving direct and inverse proportionality.
Introduction to Direct and Inverse Variation
Before diving into the combined variation of y varying directly as x and inversely as z, let's establish a firm understanding of direct and inverse variations individually.
Direct Variation: Two variables are said to be in direct variation if an increase in one variable causes a proportional increase in the other, and a decrease in one causes a proportional decrease in the other. Mathematically, this is represented as:
y = kx
where:
- y and x are the variables.
- k is the constant of proportionality. This constant represents the rate of change between the variables.
For example, the distance traveled (y) is directly proportional to the speed (x) if the time remains constant. A faster speed (increased x) results in a greater distance covered (increased y).
Inverse Variation: Two variables are in inverse variation (or indirect variation) if an increase in one variable causes a proportional decrease in the other, and vice versa. The mathematical representation is:
y = k/x
where:
- y and x are the variables.
- k is the constant of proportionality.
Consider the relationship between speed (x) and time (y) to travel a fixed distance. If you increase your speed (increased x), the time taken to travel the distance (y) decreases.
Combining Direct and Inverse Variation: y varies directly as x and inversely as z
Now, let's combine these concepts. When we say "y varies directly as x and inversely as z," it means that y increases proportionally with x but decreases proportionally with z. The mathematical formula representing this combined variation is:
y = kx/z
where:
- y, x, and z are the variables.
- k is the constant of proportionality.
This equation implies that:
- If x increases, y increases (direct proportionality with x).
- If z increases, y decreases (inverse proportionality with z).
This type of variation is commonly encountered in real-world scenarios. For example, the force of gravity (y) varies directly with the product of the masses of two objects (x) and inversely with the square of the distance between them (z).
Solving Problems Involving Combined Variation
Solving problems involving combined variation generally requires a two-step process:
-
Finding the constant of proportionality (k): This step involves using a given set of values for x, y, and z to solve for k in the equation y = kx/z.
-
Using k to solve for an unknown variable: Once k is determined, you can use the equation with the known value of k to find the unknown variable (either x, y, or z) given other values.
Let's illustrate with an example:
Problem: The volume (V) of a gas varies directly as its temperature (T) and inversely as its pressure (P). If V = 10 liters when T = 200 Kelvin and P = 5 atmospheres, find the volume when T = 300 Kelvin and P = 10 atmospheres.
Solution:
- Find k: The relationship is V = kT/P. Substitute the given values:
10 = k(200)/5
Solving for k, we get:
k = (10 * 5) / 200 = 1/4
- Find V for new conditions: Now that we have k = 1/4, we can use the equation V = (1/4)T/P with the new values of T and P:
V = (1/4)(300)/10 = 7.5 liters
Therefore, the volume of the gas will be 7.5 liters under the new conditions.
Real-World Applications of Combined Variation
The concept of y varying directly as x and inversely as z has numerous applications across various disciplines:
-
Physics: As mentioned earlier, Newton's Law of Universal Gravitation exemplifies this type of variation. The force of gravity is directly proportional to the product of the masses and inversely proportional to the square of the distance between them. Similarly, many concepts in electricity and magnetism involve combined variations.
-
Engineering: Designing structures and systems often requires considering factors that vary both directly and inversely. For instance, the strength of a beam might be directly proportional to its width and inversely proportional to its length.
-
Economics: Supply and demand models sometimes incorporate combined variation. The price of a commodity might vary directly with demand and inversely with supply.
-
Chemistry: In chemical reactions, the rate of reaction can be influenced by factors that exhibit both direct and inverse proportionality.
Addressing Common Misconceptions
A frequent mistake is incorrectly interpreting the relationship between the variables. Remember that:
- Direct variation implies a proportional increase or decrease between variables.
- Inverse variation means an increase in one variable leads to a proportional decrease in the other, and vice versa.
- In combined variation, both relationships must be considered simultaneously.
It's essential to carefully analyze the problem statement to identify which variable varies directly and which varies inversely. Incorrect identification will lead to incorrect solutions.
Further Exploration: More Complex Variations
While we focused on the case where y varies directly as x and inversely as z, combined variations can involve more variables. For instance, y could vary directly as x and inversely as the product of z and w:
y = kx/(zw)
The principles remain the same; you would still need to find the constant of proportionality k using a given set of values and then use it to solve for an unknown variable. The complexity increases with the number of variables, but the underlying concepts remain consistent.
Frequently Asked Questions (FAQ)
Q1: What if the problem doesn't explicitly state "varies directly" or "varies inversely"?
A1: The problem statement might describe the relationship using words like "proportional to," "inversely proportional to," or phrases that imply a direct or inverse relationship. Carefully read the problem and identify the nature of the relationships between the variables.
Q2: Can k be negative?
A2: Yes, k can be negative. A negative k indicates an inverse relationship between the variables, even in a combined variation scenario. For example, if y = -kx/z, an increase in x would lead to a decrease in y, considering the negative sign.
Q3: How do I handle situations with exponents?
A3: When variables are raised to powers, the equation adapts accordingly. For example, if y varies directly as the square of x and inversely as the cube of z, the equation becomes: y = kx²/z³. The methods for solving remain the same; you still find k using known values and then use it to solve for unknowns.
Conclusion
Understanding how y varies directly as x and inversely as z is essential for effectively modeling and solving problems in diverse fields. By mastering the principles of direct and inverse variation and their combination, you develop a valuable problem-solving skill applicable in many areas of study and work. Remember to carefully interpret the problem statements, identify the relationships between variables, and systematically solve for the constant of proportionality to accurately determine unknown quantities. This comprehensive approach will build a strong foundation for tackling more complex variation problems in the future.
Latest Posts
Latest Posts
-
Can I Use Calculator On Teas Test
Sep 16, 2025
-
Order Of Operations With Distributive Property
Sep 16, 2025
-
Compared To Wave A Wave B Has A
Sep 16, 2025
-
Perimeter Of A Triangle With Points
Sep 16, 2025
-
Boyles Law Describes The Relationship Between The
Sep 16, 2025
Related Post
Thank you for visiting our website which covers about Y Varies Directly As X And Inversely As Z . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.