Write 1/8 As A Decimal Number.
faraar
Sep 20, 2025 · 6 min read
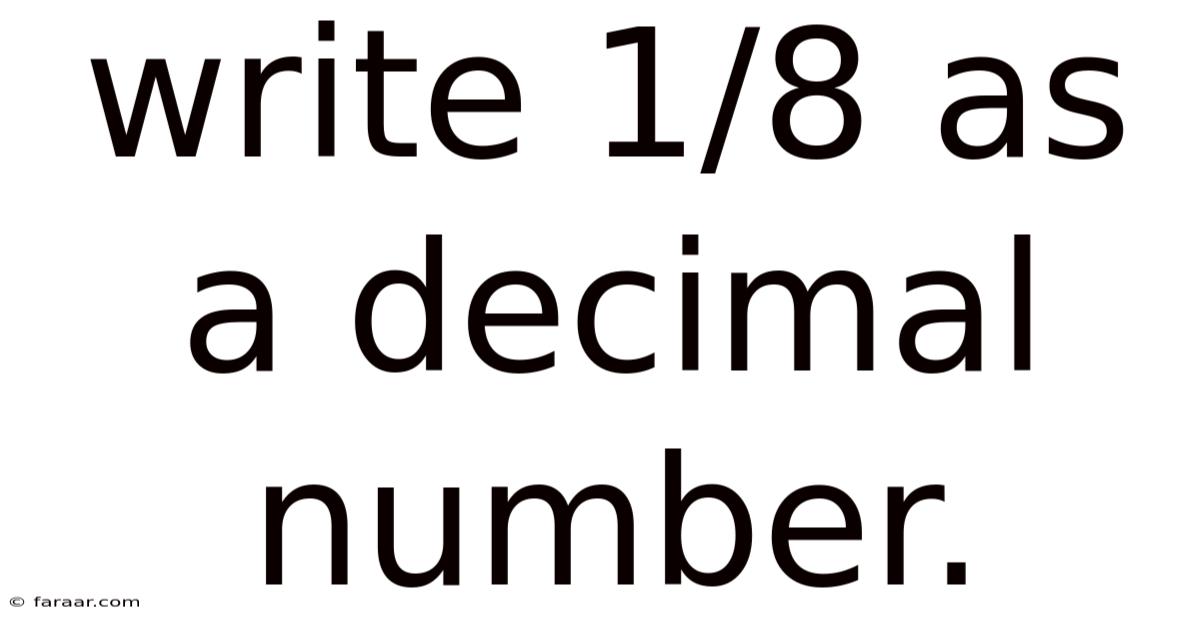
Table of Contents
Writing 1/8 as a Decimal Number: A Comprehensive Guide
Many find working with fractions challenging, but understanding how to convert them to decimals is a crucial skill in mathematics and everyday life. This comprehensive guide will walk you through the process of converting the fraction 1/8 into its decimal equivalent, exploring various methods and offering insights into the underlying mathematical principles. We'll cover not only the 'how' but also the 'why,' ensuring a solid grasp of this fundamental concept. This article will also delve into related topics, providing a broader understanding of fraction-to-decimal conversions and their applications.
Understanding Fractions and Decimals
Before we dive into the conversion process, let's briefly review the concepts of fractions and decimals. A fraction represents a part of a whole, expressed as a ratio of two numbers: the numerator (top number) and the denominator (bottom number). For example, in the fraction 1/8, 1 is the numerator and 8 is the denominator. This means we are considering one out of eight equal parts.
A decimal is a way of writing a number that uses a base-ten system. The digits to the right of the decimal point represent tenths, hundredths, thousandths, and so on. For example, 0.5 represents five tenths (5/10), and 0.25 represents twenty-five hundredths (25/100).
The key to converting a fraction to a decimal is to understand that both represent the same value – just expressed differently. Converting a fraction to a decimal essentially means finding the equivalent decimal representation of that fraction.
Method 1: Direct Division
The most straightforward method to convert 1/8 to a decimal is through direct division. The fraction 1/8 essentially represents the division problem 1 ÷ 8. Using long division or a calculator:
1 ÷ 8 = 0.125
Therefore, 1/8 expressed as a decimal is 0.125.
This method is simple and effective, especially for fractions with relatively small denominators. It relies on the fundamental understanding that a fraction is a division problem.
Method 2: Finding an Equivalent Fraction with a Denominator of 10, 100, 1000, etc.
Another approach involves finding an equivalent fraction with a denominator that is a power of 10 (10, 100, 1000, and so on). This allows for a direct conversion to a decimal. While this method isn't always possible (some fractions don't have an equivalent with a power-of-10 denominator), it's a useful technique when applicable.
Unfortunately, 1/8 doesn't easily convert to an equivalent fraction with a denominator of 10, 100, or 1000. We could try multiplying both the numerator and denominator by various numbers, but we'll always end up with a remainder. This demonstrates that this method isn't always the most efficient approach.
Method 3: Understanding Decimal Place Value
Understanding decimal place value is key to interpreting decimal numbers. The digit immediately to the right of the decimal point represents tenths, the next digit represents hundredths, then thousandths, and so on.
In the case of 0.125, we have:
- 0.1: One tenth (1/10)
- 0.02: Two hundredths (2/100)
- 0.005: Five thousandths (5/1000)
Adding these together, we get 1/10 + 2/100 + 5/1000 = 125/1000. If we simplify this fraction by dividing both the numerator and the denominator by 125, we get 1/8. This illustrates the equivalence between the decimal 0.125 and the fraction 1/8.
Illustrative Examples: Converting Other Simple Fractions to Decimals
Let's look at a few more examples to solidify the understanding of fraction-to-decimal conversions.
- 1/2: This is easily converted to a decimal by recognizing that 1/2 is equivalent to 5/10, which is 0.5.
- 1/4: Similar to 1/2, 1/4 is equivalent to 25/100, giving us 0.25.
- 3/4: This is equivalent to 75/100, resulting in the decimal 0.75.
- 1/5: This is equivalent to 2/10, resulting in the decimal 0.2.
- 1/10: This is directly 0.1.
These examples demonstrate that some fractions convert easily to decimals, particularly those with denominators that are factors of powers of 10.
Applications of Decimal Conversions
Converting fractions to decimals is a crucial skill with widespread applications in various fields:
- Finance: Calculating percentages, interest rates, and discounts often involves working with decimals.
- Science: Measuring quantities and expressing results in scientific notation often necessitates decimal conversions.
- Engineering: Precision measurements and calculations in engineering projects rely heavily on decimals.
- Everyday Life: Many everyday calculations, from calculating tips to sharing expenses, benefit from an understanding of decimals.
Mastering this skill enhances problem-solving abilities and provides a deeper understanding of numerical representation.
Addressing Potential Challenges and Misconceptions
A common misconception is that all fractions can be easily converted to terminating decimals (decimals that end). This isn't true; some fractions, when converted to decimals, result in repeating decimals (decimals with a pattern of digits that repeats infinitely). For instance, 1/3 converts to 0.3333... (the 3 repeats indefinitely).
Another challenge is dealing with larger numbers in the numerator or denominator. While the division method works for any fraction, it can become more time-consuming with larger numbers. In these cases, calculators are invaluable tools.
Frequently Asked Questions (FAQ)
Q: Is 0.125 the only decimal representation of 1/8?
A: Yes, 0.125 is the only decimal representation of 1/8. This is a terminating decimal, meaning it has a finite number of digits.
Q: Can I convert any fraction to a decimal?
A: Yes, every fraction can be converted to a decimal through division. However, the resulting decimal may be terminating or repeating.
Q: What is the best method for converting fractions to decimals?
A: Direct division is generally the most efficient and versatile method for converting any fraction to a decimal. Finding an equivalent fraction with a power-of-10 denominator is useful for certain fractions but not universally applicable.
Q: What if I get a repeating decimal? How do I handle that?
A: Repeating decimals are a valid representation of some fractions. You can represent them using a bar over the repeating digits (e.g., 0.333... is written as 0.̅3). Sometimes, you may round the repeating decimal to a certain number of decimal places for practical purposes.
Q: Are there any online tools or calculators that can help me with this conversion?
A: While this article encourages understanding the underlying mathematical principles, many online calculators and converters are readily available to assist with fraction-to-decimal conversions.
Conclusion
Converting the fraction 1/8 to a decimal number, which is 0.125, is a fundamental concept in mathematics with practical applications in various fields. This guide has explored multiple methods for achieving this conversion, highlighting the importance of understanding both fractions and decimals and their relationship to each other. By grasping these concepts and techniques, you'll enhance your numerical literacy and build a strong foundation for more advanced mathematical studies. Remember, practice is key! The more you work with fractions and decimals, the more comfortable and proficient you will become.
Latest Posts
Latest Posts
-
How To Take Ln Of Both Sides
Sep 20, 2025
-
Which Substance Can Be Broken Down By A Chemical Change
Sep 20, 2025
-
Does H2o Have Dipole Dipole Forces
Sep 20, 2025
-
1 10 000 As A Power Of 10
Sep 20, 2025
-
For The Chemical Equation So2 No2
Sep 20, 2025
Related Post
Thank you for visiting our website which covers about Write 1/8 As A Decimal Number. . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.