1/10 000 As A Power Of 10
faraar
Sep 20, 2025 · 7 min read
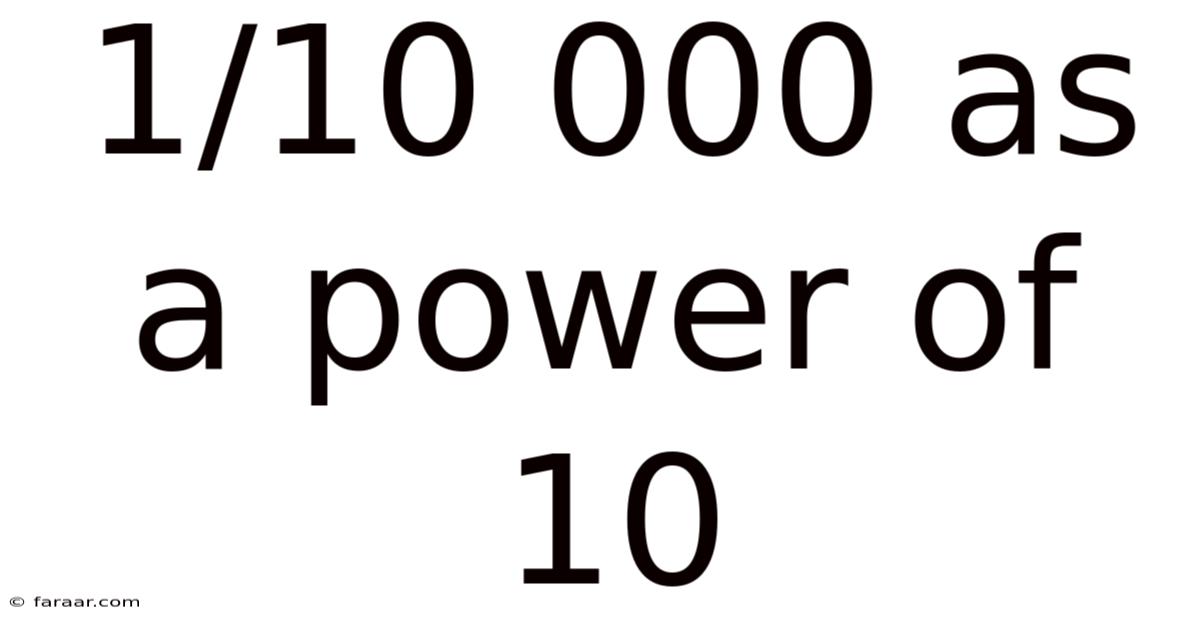
Table of Contents
Understanding 1/10,000 as a Power of 10: A Deep Dive into Scientific Notation
Have you ever wondered how to express incredibly small numbers in a concise and manageable way? Scientists and mathematicians frequently encounter minuscule values, and expressing them as powers of 10, also known as scientific notation, provides a powerful tool for simplification and clarity. This article delves into the representation of 1/10,000 as a power of 10, exploring the underlying principles and applications of this essential mathematical concept. We'll move beyond the simple answer and explore the broader implications of working with very small numbers in scientific contexts.
Introduction: Why Powers of 10 Matter
Scientific notation is a standardized way of writing numbers that are either very large or very small. It utilizes powers of 10 to express these numbers efficiently. Instead of writing out lengthy strings of zeros, we use exponents to represent the magnitude of the number. This method significantly simplifies calculations and improves readability, particularly in fields like physics, chemistry, and engineering where incredibly large or small numbers are commonplace.
For instance, the distance to the sun is approximately 150,000,000,000 meters. In scientific notation, this is written as 1.5 x 10<sup>11</sup> meters. This representation is far more concise and manageable than the original number. Similarly, extremely small values, like the size of an atom (on the order of 10<sup>-10</sup> meters), are easily expressed and compared using this system.
Expressing 1/10,000 as a Power of 10
The fraction 1/10,000 can be readily expressed as a decimal: 0.0001. To convert this decimal to scientific notation, we need to move the decimal point four places to the right until we have a number between 1 and 10. Each place we move the decimal point represents a power of 10. Since we moved the decimal point four places to the right, the exponent of 10 will be -4.
Therefore, 1/10,000 = 0.0001 = 1 x 10<sup>-4</sup>.
This signifies that 1/10,000 is one ten-thousandth, or one multiplied by ten raised to the power of negative four. The negative exponent indicates that the number is smaller than one.
Understanding Negative Exponents
A crucial aspect of understanding scientific notation involves grasping the concept of negative exponents. A negative exponent indicates the reciprocal of the positive exponent. In simpler terms:
- 10<sup>2</sup> = 100
- 10<sup>-2</sup> = 1/10<sup>2</sup> = 1/100 = 0.01
The negative sign doesn't imply a negative number; instead, it denotes a fraction or a number less than one. The magnitude of the number decreases as the negative exponent increases.
For example:
- 10<sup>-1</sup> = 0.1 (one tenth)
- 10<sup>-2</sup> = 0.01 (one hundredth)
- 10<sup>-3</sup> = 0.001 (one thousandth)
- 10<sup>-4</sup> = 0.0001 (one ten-thousandth)
Calculations with Powers of 10
Scientific notation simplifies calculations involving very large or very small numbers. When multiplying or dividing numbers in scientific notation, we follow these rules:
-
Multiplication: Multiply the coefficients and add the exponents.
- (a x 10<sup>m</sup>) x (b x 10<sup>n</sup>) = (a x b) x 10<sup>(m+n)</sup>
-
Division: Divide the coefficients and subtract the exponents.
- (a x 10<sup>m</sup>) / (b x 10<sup>n</sup>) = (a / b) x 10<sup>(m-n)</sup>
Let's illustrate with an example:
(2 x 10<sup>3</sup>) x (5 x 10<sup>-2</sup>) = (2 x 5) x 10<sup>(3 + (-2))</sup> = 10 x 10<sup>1</sup> = 1 x 10<sup>2</sup> = 100
This demonstrates how efficiently scientific notation simplifies complex calculations.
Applications of Scientific Notation: Real-World Examples
The application of scientific notation extends far beyond the classroom. Consider these real-world scenarios:
-
Astronomy: Distances in space are vast. Expressing these distances in standard notation would be cumbersome. Scientific notation allows astronomers to easily represent distances to stars and galaxies (e.g., light-years).
-
Chemistry: The number of atoms and molecules in even a small amount of substance is enormous. Scientific notation provides a convenient method for representing these quantities (e.g., Avogadro's number, 6.022 x 10<sup>23</sup>).
-
Physics: Subatomic particles are incredibly tiny. Scientific notation provides a practical way to handle their sizes and masses.
-
Computer Science: Computers often work with extremely large or small numbers, especially in data processing and simulations. Scientific notation aids in handling such numbers efficiently.
-
Engineering: In various engineering disciplines, especially those dealing with electrical circuits and signal processing, dealing with small voltages and currents necessitates the use of scientific notation.
Comparing Numbers in Scientific Notation
Scientific notation simplifies the comparison of very large or very small numbers. When comparing two numbers expressed in scientific notation, we compare the exponents first. The number with the larger exponent is generally larger, provided the coefficients are of comparable magnitude. If the exponents are the same, we then compare the coefficients.
For instance:
- 2 x 10<sup>5</sup> is larger than 8 x 10<sup>4</sup> (because 5 > 4).
- 8 x 10<sup>4</sup> is larger than 2 x 10<sup>4</sup> (because 8 > 2).
Beyond the Basics: Significant Figures and Precision
When working with scientific notation, it's crucial to consider significant figures. Significant figures indicate the precision of a measurement. The number of significant figures in a measurement reflects the accuracy of the measuring instrument and the uncertainty involved in the measurement process. For instance, 1.000 x 10<sup>-4</sup> implies a higher degree of precision than 1 x 10<sup>-4</sup>.
Converting Between Scientific Notation and Standard Notation
Converting between standard notation and scientific notation involves shifting the decimal point and adjusting the exponent accordingly.
-
Standard to Scientific: Move the decimal point to obtain a number between 1 and 10. The number of places moved determines the exponent. If the decimal point moves to the left, the exponent is positive; if it moves to the right, the exponent is negative.
-
Scientific to Standard: Move the decimal point according to the exponent. A positive exponent indicates a movement to the right; a negative exponent indicates a movement to the left.
Frequently Asked Questions (FAQ)
Q1: What is the difference between 10<sup>-4</sup> and -10<sup>4</sup>?
A1: 10<sup>-4</sup> represents one ten-thousandth (0.0001), while -10<sup>4</sup> represents negative ten thousand (-10,000). The negative sign in the exponent indicates a fraction, whereas the negative sign before the base indicates a negative number.
Q2: Can I use scientific notation for all numbers?
A2: While you technically can, it's generally not necessary for numbers that are easily expressed in standard notation. Scientific notation is most useful for extremely large or small numbers where it enhances clarity and simplifies calculations.
Q3: How do I perform addition and subtraction with numbers in scientific notation?
A3: For addition and subtraction, you must ensure the numbers have the same exponent before adding or subtracting the coefficients. You might need to rewrite one or both numbers to achieve this.
Conclusion: Mastering Scientific Notation for a Deeper Understanding
Understanding how to express 1/10,000 as a power of 10 (1 x 10<sup>-4</sup>) is a fundamental step in grasping the power and utility of scientific notation. This method provides a concise, efficient, and accurate way to represent and manipulate incredibly small (and large) numbers across numerous scientific and engineering disciplines. By mastering the concepts outlined in this article, you'll not only improve your mathematical skills but also gain a deeper appreciation for the vast scales involved in the natural world and the tools scientists use to understand them. The ability to confidently convert between decimal form, fractional form, and scientific notation is a key skill for anyone pursuing STEM fields or any area involving quantitative analysis.
Latest Posts
Latest Posts
-
Choose The Solution To The Equation Mc001 1 Jpg Mc001 2 Jpg Mc001 3 Jpg
Sep 20, 2025
-
How To Improve English Score On Act
Sep 20, 2025
-
Find All Solutions Of The Equation
Sep 20, 2025
-
How To Order Concrete In Yards
Sep 20, 2025
-
45 Is 30 Of What Number
Sep 20, 2025
Related Post
Thank you for visiting our website which covers about 1/10 000 As A Power Of 10 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.