Which Is The Correct Graph Of The Inequality Y 2x+1
faraar
Sep 22, 2025 · 6 min read
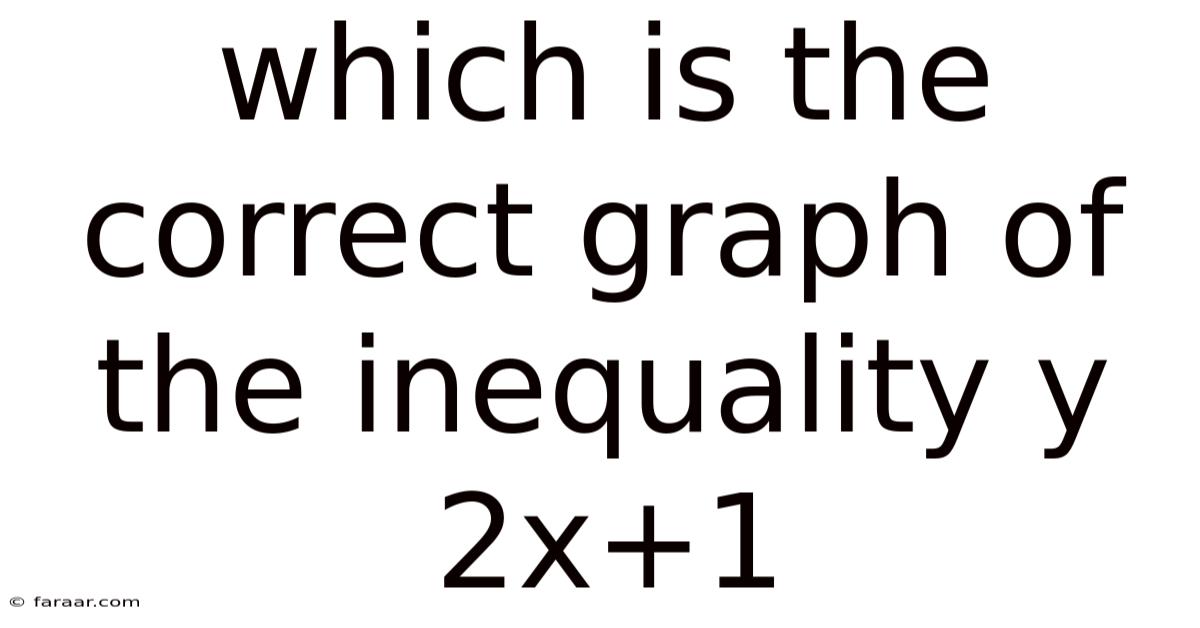
Table of Contents
Decoding the Inequality: Understanding the Graph of y ≥ 2x + 1
Understanding how to graph inequalities is a crucial skill in algebra. This article will delve into the process of graphing the linear inequality y ≥ 2x + 1, explaining not only the steps involved but also the underlying mathematical principles. We'll cover how to interpret the inequality, how to plot the boundary line, and how to shade the correct region representing all the solutions. By the end, you’ll be confident in graphing similar inequalities and understanding the meaning behind the graphical representation.
Introduction: Linear Inequalities and Their Graphs
A linear inequality, unlike a linear equation, doesn't represent a single line but rather a region on the coordinate plane. The inequality y ≥ 2x + 1 states that the value of y must be greater than or equal to the value of 2x + 1. This means there's an infinite number of points (x, y) that satisfy this condition. Graphing helps visualize this infinite set of solutions. The key to understanding the graph lies in recognizing the boundary line and the direction of the shaded region.
Step-by-Step Guide to Graphing y ≥ 2x + 1
Let's break down the graphing process into manageable steps:
1. Treat the Inequality as an Equation:
First, we treat the inequality y ≥ 2x + 1 as if it were an equation: y = 2x + 1. This gives us the boundary line of our inequality. This line separates the coordinate plane into two regions: one where the inequality y ≥ 2x + 1 is true, and one where it's false.
2. Identify the y-intercept and Slope:
The equation y = 2x + 1 is in slope-intercept form (y = mx + b), where m is the slope and b is the y-intercept. In this case:
m = 2(the slope)b = 1(the y-intercept)
The y-intercept means the line crosses the y-axis at the point (0, 1). The slope of 2 means that for every 1 unit increase in x, y increases by 2 units.
3. Plot the Boundary Line:
Using the y-intercept and slope, we can plot the boundary line. Start at the point (0, 1). Since the slope is 2, move 1 unit to the right and 2 units up to find another point on the line (1, 3). Plot these points and draw a straight line through them. Because the inequality includes "or equal to" (≥), the line itself is part of the solution set, so we draw it as a solid line. If the inequality were y > 2x + 1 (strictly greater than), we would draw a dashed line to indicate that the line itself is not included in the solution.
4. Determine the Shaded Region:
This is the crucial step. The inequality y ≥ 2x + 1 tells us that we want all the points where the y-coordinate is greater than or equal to the corresponding value on the line. To find the correct region, we can use a test point. A convenient test point is the origin (0, 0). Substitute the coordinates of the origin into the inequality:
0 ≥ 2(0) + 1
0 ≥ 1
This statement is false. Since the test point (0, 0) does not satisfy the inequality, the region containing (0, 0) is not part of the solution. Therefore, we shade the region above the line.
Graphical Representation and Interpretation
The correct graph of y ≥ 2x + 1 shows a solid line passing through (0, 1) with a slope of 2. The region above and including this line is shaded. Every point within the shaded region represents a pair of (x, y) values that satisfy the inequality y ≥ 2x + 1. For example, the point (2, 5) lies within the shaded region because 5 ≥ 2(2) + 1 (5 ≥ 5), which is true. The point (-1, -1) lies outside the shaded region because -1 ≥ 2(-1) + 1 (-1 ≥ -1), which is false. Therefore, the shaded region accurately represents all possible solutions to the inequality.
Understanding the Mathematical Concepts
The process of graphing inequalities hinges on several key mathematical concepts:
- Linear Equations: The foundation of graphing inequalities lies in understanding linear equations and their representation on a coordinate plane. The boundary line is derived directly from the corresponding linear equation.
- Slope and Intercept: The slope and y-intercept are essential for quickly plotting the boundary line. Understanding these concepts streamlines the graphing process.
- Inequality Symbols: The meaning of inequality symbols (>, <, ≥, ≤) is critical. These symbols determine whether the boundary line is solid or dashed and which region to shade.
- Test Points: Using test points allows for a systematic way to determine which region satisfies the inequality. Any point not on the line can be used as a test point.
Common Mistakes to Avoid
Several common mistakes can lead to incorrect graphs:
- Confusing the Inequality Symbols: Mistaking ">" for "≥" or "<" for "≤" will result in the wrong type of line (dashed instead of solid or vice versa) and potentially the wrong shaded region.
- Incorrect Shading: Failing to correctly identify the region that satisfies the inequality is a frequent error. Always use a test point to confirm the shading.
- Ignoring the Boundary Line: For inequalities with "≥" or "≤," remember to include the boundary line as part of the solution by drawing a solid line.
Frequently Asked Questions (FAQ)
Q: What if the inequality is y < 2x + 1? How does the graph change?
A: The boundary line would remain the same (a line with a slope of 2 and y-intercept of 1), but it would be a dashed line because the inequality is strictly less than. The shaded region would be the area below the line.
Q: Can I use any point as a test point?
A: Yes, any point not on the boundary line can be used as a test point. However, the origin (0,0) is often the easiest to use because it simplifies the calculation.
Q: What if the inequality is not in slope-intercept form?
A: If the inequality is not in slope-intercept form (y = mx + b), you can rearrange it to that form or use other graphing methods like finding the x and y intercepts.
Q: How do I graph inequalities with more than one variable?
A: Graphing inequalities with more than one variable involves understanding systems of inequalities and involves shading regions where all the inequalities are satisfied simultaneously. This requires a more advanced understanding of linear programming.
Conclusion: Mastering Inequality Graphs
Graphing linear inequalities is a fundamental skill in algebra. By understanding the steps involved—treating the inequality as an equation to find the boundary line, using the slope and intercept to plot the line, and using a test point to determine the shaded region—you can accurately and confidently graph any linear inequality. Remember to pay close attention to the inequality symbols and use a test point to avoid common mistakes. The graphical representation not only visually displays the solution set but also provides a deeper understanding of the underlying mathematical relationships. With practice, graphing inequalities will become second nature, enhancing your problem-solving skills in algebra and beyond.
Latest Posts
Latest Posts
-
Which Of The Following Has The Largest Second Ionization Energy
Sep 22, 2025
-
Write An Equation For The Line Graphed Below
Sep 22, 2025
-
How To Factor Polynomials With A Coefficient
Sep 22, 2025
-
The Sum Of 3 And Four Times A Number
Sep 22, 2025
-
Do Valence Electrons Have The Most Energy
Sep 22, 2025
Related Post
Thank you for visiting our website which covers about Which Is The Correct Graph Of The Inequality Y 2x+1 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.