The Sum Of 3 And Four Times A Number
faraar
Sep 22, 2025 · 7 min read
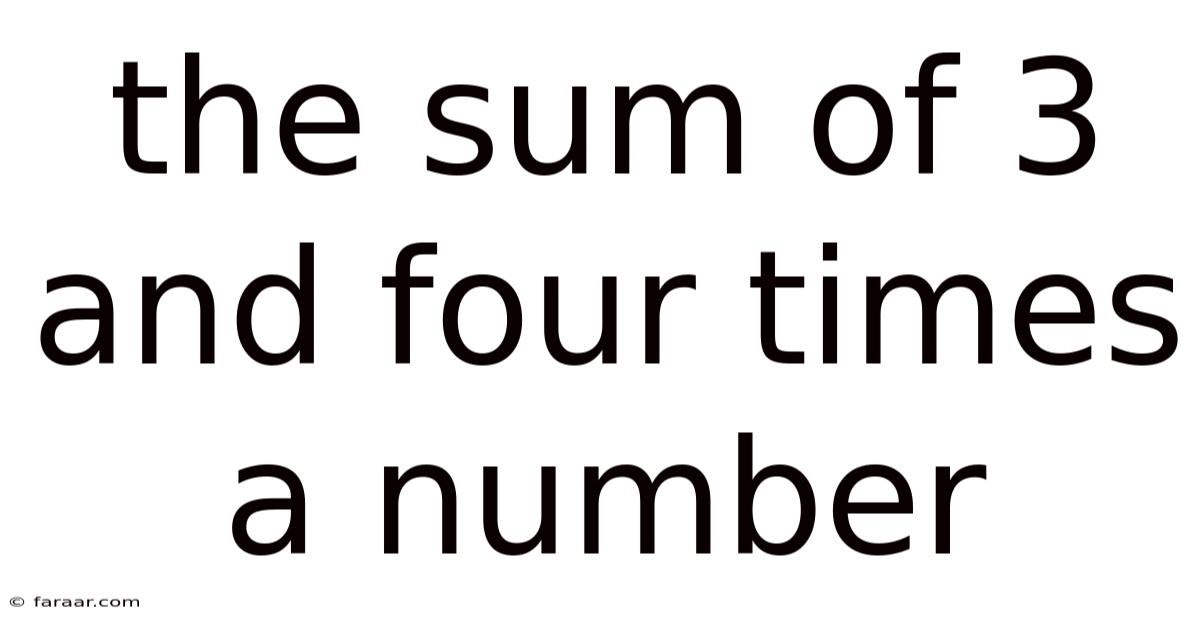
Table of Contents
Unraveling the Mystery: The Sum of 3 and Four Times a Number
Understanding algebraic expressions is a fundamental building block in mathematics. This article delves into the seemingly simple yet incredibly important concept of "the sum of 3 and four times a number." We'll explore its representation, manipulation, and applications, providing a comprehensive guide for students of all levels, from beginners grappling with basic algebra to those seeking a deeper understanding of mathematical concepts. This exploration will cover various aspects including translating word problems, solving equations, and understanding the broader implications of this type of algebraic expression within more complex mathematical scenarios.
Understanding the Expression: Breaking it Down
The phrase "the sum of 3 and four times a number" might initially seem daunting, but it can be easily broken down into its constituent parts. Let's dissect it step-by-step:
-
A number: This represents an unknown value, typically denoted by a variable, most commonly x. However, any letter can be used.
-
Four times a number: This translates to 4 multiplied by the number, or 4*x (or simply 4x).
-
The sum of 3 and four times a number: This indicates the addition of 3 and 4x. Therefore, the complete algebraic expression is 3 + 4x.
This seemingly simple expression forms the basis for countless mathematical problems and real-world applications. Understanding its construction is crucial for progressing to more advanced algebraic concepts.
Representing the Expression Graphically
Visualizing mathematical concepts can significantly enhance understanding. The expression 3 + 4x can be represented graphically in several ways. The most common method is using a Cartesian coordinate system to plot the linear equation y = 3 + 4x. This creates a straight line with a y-intercept of 3 (the point where the line crosses the y-axis) and a slope of 4 (representing the rate of change of y with respect to x). Each point on this line represents a solution to the equation, showing the relationship between x and y.
For instance, if x = 1, then y = 3 + 4(1) = 7. This means the point (1,7) lies on the line. Similarly, if x = 2, y = 11, resulting in the point (2,11). By plotting several such points and connecting them, the line representing the equation y = 3 + 4x is generated. This visual representation provides an intuitive understanding of how the value of y changes as x varies.
Solving Equations Involving the Expression
The expression 3 + 4x frequently appears within equations that need solving. Let's examine a few examples:
Example 1: Finding the value of x
Suppose we have the equation: 3 + 4x = 19. To solve for x, we need to isolate x on one side of the equation. This involves performing the inverse operations in reverse order of operations (PEMDAS/BODMAS):
- Subtract 3 from both sides: 4x = 16
- Divide both sides by 4: x = 4
Therefore, the solution to the equation 3 + 4x = 19 is x = 4.
Example 2: A more complex equation
Consider the equation: 2(3 + 4x) + 5 = 21. Here, we need to follow the order of operations:
- Distribute the 2: 6 + 8x + 5 = 21
- Combine like terms: 11 + 8x = 21
- Subtract 11 from both sides: 8x = 10
- Divide both sides by 8: x = 10/8 = 5/4 or 1.25
Thus, the solution to the equation 2(3 + 4x) + 5 = 21 is x = 5/4 or 1.25.
Example 3: Equations with variables on both sides
Solving equations where the expression appears on both sides requires a slightly different approach. For instance, consider: 3 + 4x = 11 + 2x.
- Subtract 2x from both sides: 2 + 4x = 11
- Subtract 3 from both sides: 2x = 8
- Divide both sides by 2: x = 4
These examples illustrate the versatility of the expression 3 + 4x in different equation contexts. Mastering these techniques is essential for progressing to more intricate algebraic problems.
Real-World Applications
The seemingly simple expression 3 + 4x has far-reaching real-world applications across various disciplines. Here are a few examples:
-
Calculating Costs: Imagine you're renting a car. The rental fee is $3 plus $4 per hour. The total cost (y) after renting the car for x hours can be represented by the equation y = 3 + 4x. This allows easy calculation of the total cost based on the rental duration.
-
Determining Earnings: Suppose you earn a base salary of $3 per day plus $4 for each item you sell. Your total daily earnings (y) can be calculated using the expression y = 3 + 4x, where x represents the number of items sold.
-
Modeling Growth: In certain biological or economic contexts, the expression can model growth where 3 represents an initial value and 4 represents a growth rate. For example, a population starting at 3 individuals that grows by 4 individuals each generation can be modeled by this expression.
-
Physics and Engineering: Linear relationships are ubiquitous in physics and engineering. Many physical quantities are related linearly, and the expression 3 + 4x might represent the relationship between two variables in a given system, such as distance traveled given initial displacement and velocity.
These examples demonstrate the practical relevance of the expression 3 + 4x in diverse real-world situations. The ability to translate word problems into algebraic expressions like this is a fundamental skill in applied mathematics.
Expanding the Concept: More Complex Scenarios
The foundation laid with the expression 3 + 4x can be expanded to encompass more complex algebraic scenarios. For instance:
-
Polynomials: The expression can be incorporated into higher-degree polynomials. For example, (3 + 4x)² or (3 + 4x)(x + 2) would involve expanding and simplifying these expressions using the distributive property and other algebraic rules.
-
Inequalities: Instead of an equation, the expression could be part of an inequality, such as 3 + 4x > 15. Solving these inequalities involves similar steps to solving equations, but the solution will be a range of values rather than a single value.
-
Systems of Equations: The expression might be part of a system of equations, requiring the simultaneous solution of multiple equations involving this expression and other related expressions.
-
Calculus: In calculus, the expression can be used in differential and integral calculus to find derivatives and integrals, respectively. Understanding derivatives would reveal the instantaneous rate of change of the expression with respect to x, while integration would show the area under the curve of the function y = 3 + 4x.
These advanced applications demonstrate that the fundamental understanding of "the sum of 3 and four times a number" lays the groundwork for much more complex mathematical modeling and problem-solving.
Frequently Asked Questions (FAQ)
Q1: What if the expression was "the sum of four times a number and 3"?
A1: This is equivalent to the original expression. Addition is commutative, meaning the order doesn't change the result. So, 3 + 4x is the same as 4x + 3.
Q2: Can the variable be a letter other than x?
A2: Absolutely! Any letter can represent the unknown number, such as y, z, a, b, etc. The expression could be written as 3 + 4y, 3 + 4z, and so on.
Q3: What if the problem involved subtraction instead of addition?
A3: The expression would change. For instance, "the difference between 3 and four times a number" would be represented as 3 - 4x. The order matters here because subtraction is not commutative.
Q4: How do I know when to use this expression in a real-world problem?
A4: Look for situations where a constant value is added to a value that's proportional to another variable. The constant represents the initial value or fixed cost, while the proportional part signifies a rate or additional cost per unit.
Q5: Can this expression represent a negative number?
A5: Yes. If the value of x is negative enough, the entire expression 3 + 4x can be negative.
Conclusion
The seemingly simple algebraic expression "the sum of 3 and four times a number," represented as 3 + 4x, is a cornerstone of mathematical understanding. Its exploration reveals not only the basic principles of algebra but also its vast applicability in solving equations, modeling real-world scenarios, and forming the foundation for more complex mathematical concepts. By mastering this fundamental concept, students build a solid base for tackling more challenging mathematical problems and gaining a deeper appreciation for the power and elegance of mathematics. Remember, the key lies in understanding the underlying principles and practicing regularly to build confidence and proficiency.
Latest Posts
Latest Posts
-
Fill In The Blank To Make The Statement True
Sep 22, 2025
-
Compared To Jovian Planets Terrestrial Planets Have
Sep 22, 2025
-
Slope Of 3 4 And Y Intercept Of
Sep 22, 2025
-
What Is 1 3 Of 2 Tablespoons
Sep 22, 2025
-
How To Find Sum Of Infinite Series
Sep 22, 2025
Related Post
Thank you for visiting our website which covers about The Sum Of 3 And Four Times A Number . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.