Which Is Greater 3/4 Or 5/6
faraar
Sep 22, 2025 · 6 min read
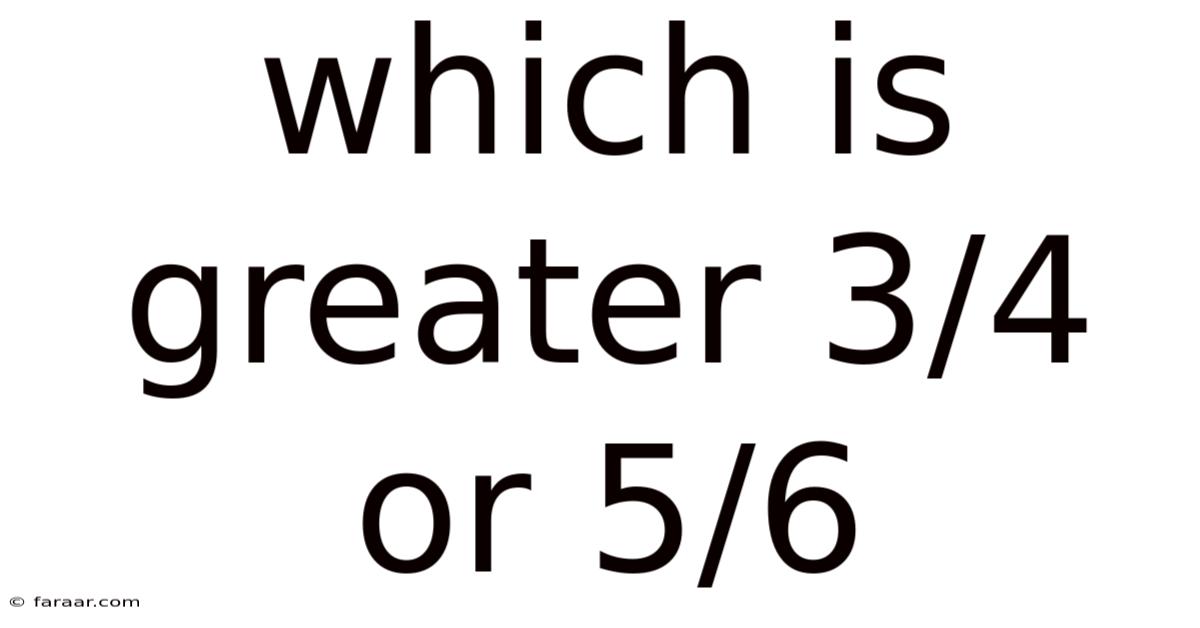
Table of Contents
Which is Greater: 3/4 or 5/6? A Deep Dive into Fraction Comparison
Determining which fraction is greater, 3/4 or 5/6, might seem like a simple task, especially for those comfortable with fractions. However, understanding the underlying principles and various methods for comparing fractions is crucial for developing a strong foundation in mathematics. This article will not only answer the question directly but also explore several methods for comparing fractions, providing you with a comprehensive understanding of this fundamental mathematical concept. We'll delve into the practical applications and even touch upon the historical context of fractions, making this a truly enriching learning experience.
Introduction: Understanding Fractions
Before we tackle the comparison, let's refresh our understanding of fractions. A fraction represents a part of a whole. It is written as a ratio of two integers, the numerator (top number) and the denominator (bottom number). The denominator indicates the total number of equal parts the whole is divided into, while the numerator indicates how many of those parts are being considered. For example, in the fraction 3/4, the denominator 4 tells us the whole is divided into four equal parts, and the numerator 3 tells us we are considering three of those parts.
Method 1: Finding a Common Denominator
The most straightforward method for comparing fractions is to find a common denominator. This involves converting both fractions into equivalent fractions with the same denominator. To do this, we find the least common multiple (LCM) of the denominators.
The denominators in our case are 4 and 6. The multiples of 4 are 4, 8, 12, 16, 20... The multiples of 6 are 6, 12, 18, 24... The least common multiple of 4 and 6 is 12.
Now, we convert both fractions to have a denominator of 12:
-
3/4: To get a denominator of 12, we multiply both the numerator and the denominator by 3 (because 4 x 3 = 12): (3 x 3) / (4 x 3) = 9/12
-
5/6: To get a denominator of 12, we multiply both the numerator and the denominator by 2 (because 6 x 2 = 12): (5 x 2) / (6 x 2) = 10/12
Now the comparison is simple: 9/12 and 10/12. Since 10 > 9, we can conclude that 5/6 is greater than 3/4.
Method 2: Converting to Decimals
Another effective method involves converting the fractions into decimals. This method is particularly useful when working with fractions that are difficult to compare using a common denominator.
To convert a fraction to a decimal, we simply divide the numerator by the denominator:
-
3/4: 3 ÷ 4 = 0.75
-
5/6: 5 ÷ 6 ≈ 0.8333...
Comparing the decimal values, 0.8333... > 0.75, confirming that 5/6 is greater than 3/4. This method is particularly helpful when dealing with fractions that don't share easily identifiable common denominators.
Method 3: Visual Representation
While not always practical for complex fractions, visual representation can be a powerful tool for understanding fraction comparison, especially for beginners. Imagine two identical pizzas.
-
Divide the first pizza into four equal slices and shade three of them (representing 3/4).
-
Divide the second pizza into six equal slices and shade five of them (representing 5/6).
By visually comparing the shaded areas, it's evident that the shaded portion of the second pizza (5/6) is larger than the shaded portion of the first pizza (3/4). This visual approach reinforces the understanding of what fractions represent.
Method 4: Cross-Multiplication
This method offers a shortcut for comparing two fractions. We cross-multiply the numerators and denominators:
-
Multiply the numerator of the first fraction by the denominator of the second fraction: 3 x 6 = 18
-
Multiply the numerator of the second fraction by the denominator of the first fraction: 5 x 4 = 20
Compare the results: 18 < 20. Since the result of the second multiplication is greater, the second fraction (5/6) is greater. This method provides a quick way to compare fractions without finding a common denominator.
Further Exploration: Understanding Fraction Magnitude
Understanding fraction magnitude goes beyond simply determining which fraction is larger. It involves grasping the relative size of the fractions in relation to the whole. Consider the following points:
-
Denominator's Influence: A larger denominator indicates smaller pieces. For example, 1/10 is smaller than 1/2 because the whole is divided into more parts.
-
Numerator's Influence: A larger numerator indicates more parts being considered. For example, 3/5 is larger than 2/5 because more parts of the whole are being considered.
-
Relationship to 1: Fractions can be easily compared to the whole (1). Fractions closer to 1 are larger. Both 3/4 and 5/6 are close to 1, but 5/6 is closer, making it larger.
Practical Applications: Where Fraction Comparison is Used
Comparing fractions isn't just an abstract mathematical exercise; it's a skill used extensively in various real-world scenarios:
-
Cooking and Baking: Following recipes often involves understanding and comparing fractions of ingredients.
-
Construction and Engineering: Precise measurements and calculations frequently require comparing fractions.
-
Finance: Understanding percentages and proportions (which are essentially fractions) is vital in financial management.
-
Data Analysis: Representing and comparing data often involves using fractions and percentages.
Frequently Asked Questions (FAQ)
Q: Is there a way to compare more than two fractions at once?
A: Yes. The most reliable method is to find the least common multiple of all the denominators and then convert all fractions to equivalent fractions with that common denominator. You can then compare the numerators.
Q: What if one fraction is a mixed number (e.g., 1 1/2)?
A: Convert the mixed number into an improper fraction. For example, 1 1/2 becomes 3/2. Then, you can apply any of the comparison methods described above.
Q: Can I use a calculator to compare fractions?
A: Yes, most calculators can handle fraction calculations. You can convert the fractions to decimals and compare the decimal values or use the fraction comparison functionality if available.
Conclusion: Mastering Fraction Comparison
Comparing fractions is a fundamental mathematical skill with wide-ranging applications. By understanding the different methods – finding a common denominator, converting to decimals, visual representation, and cross-multiplication – you'll be well-equipped to tackle fraction comparisons confidently. Remember to choose the method that best suits your comfort level and the complexity of the fractions involved. Consistent practice and a solid grasp of fraction fundamentals will solidify your understanding and enable you to apply this skill effectively in various contexts. The key takeaway is that 5/6 is definitively greater than 3/4, a fact readily demonstrated through multiple approaches. Understanding why this is true is far more important than just knowing the answer. This deeper understanding of fractions will serve you well in all your future mathematical endeavors.
Latest Posts
Latest Posts
-
Rational Number But Not An Integer
Sep 22, 2025
-
What Is The Difference Between Aas And Asa
Sep 22, 2025
-
In Photosynthesis Which Molecule Is Oxidized
Sep 22, 2025
-
Mean Of Distribution Of Sample Means
Sep 22, 2025
-
Find The X Values Where The Tangent Line Is Horizontal
Sep 22, 2025
Related Post
Thank you for visiting our website which covers about Which Is Greater 3/4 Or 5/6 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.