What Percent Is Equivalent To 2/5
faraar
Sep 11, 2025 · 5 min read
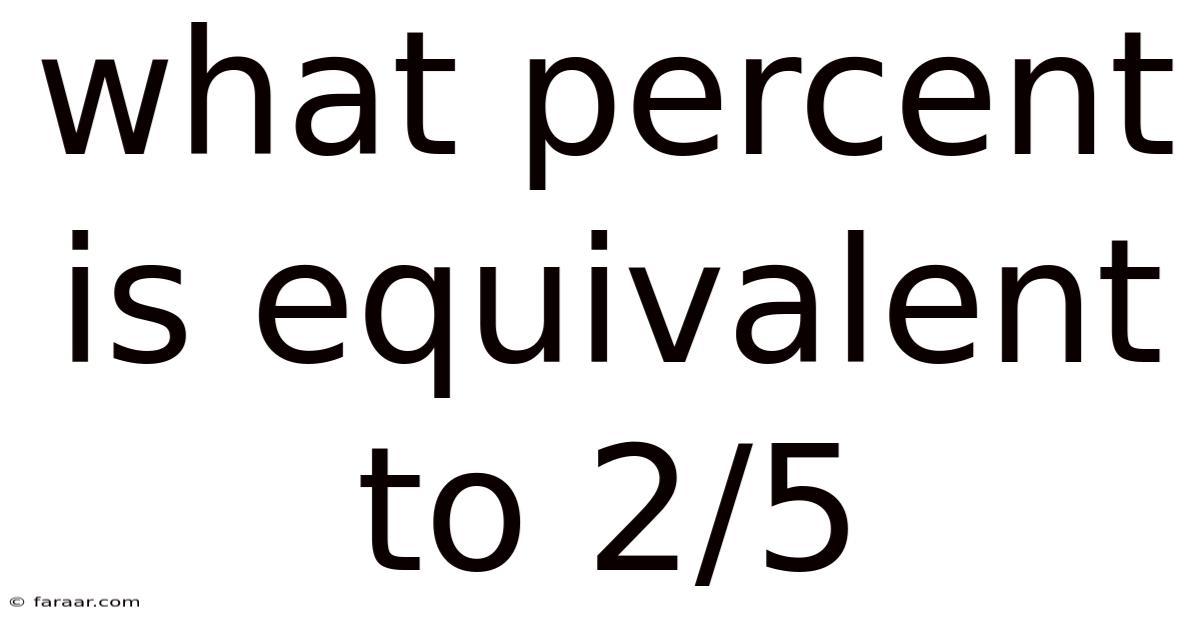
Table of Contents
What Percent is Equivalent to 2/5? A Deep Dive into Fractions, Decimals, and Percentages
Understanding the relationship between fractions, decimals, and percentages is a fundamental skill in mathematics. This article will explore how to convert the fraction 2/5 into a percentage, explaining the process step-by-step and providing a deeper understanding of the underlying concepts. We'll also delve into practical applications and address frequently asked questions to solidify your comprehension. This comprehensive guide will empower you to confidently tackle similar conversions in the future.
Introduction: Understanding the Basics
Before we dive into converting 2/5 to a percentage, let's refresh our understanding of the core concepts involved:
-
Fractions: A fraction represents a part of a whole. It's expressed as a ratio of two numbers: the numerator (top number) and the denominator (bottom number). In the fraction 2/5, 2 is the numerator and 5 is the denominator. This means we have 2 parts out of a total of 5 parts.
-
Decimals: Decimals are another way to represent parts of a whole. They use a base-ten system, with a decimal point separating the whole number from the fractional part. For example, 0.5 represents one-half (1/2).
-
Percentages: Percentages represent a fraction or decimal as parts per hundred. The symbol "%" indicates a percentage. For example, 50% means 50 out of 100, which is equivalent to 1/2 or 0.5.
Converting 2/5 to a Percentage: The Step-by-Step Process
There are two primary methods to convert the fraction 2/5 to a percentage:
Method 1: Converting the Fraction to a Decimal First
This method involves two steps:
-
Convert the fraction to a decimal: To do this, we divide the numerator (2) by the denominator (5): 2 ÷ 5 = 0.4
-
Convert the decimal to a percentage: To convert a decimal to a percentage, we multiply the decimal by 100 and add the "%" symbol: 0.4 x 100 = 40%.
Therefore, 2/5 is equivalent to 40%.
Method 2: Direct Conversion using the Proportion Method
This method directly sets up a proportion to find the equivalent percentage:
-
Set up a proportion: We know that a percentage is a fraction out of 100. So, we set up the following proportion:
2/5 = x/100
where 'x' represents the percentage we want to find.
-
Solve for x: To solve for x, we can cross-multiply:
5x = 200
-
Divide to find x: Divide both sides of the equation by 5:
x = 40
Therefore, 2/5 is equivalent to 40%.
Visual Representation: Understanding the Concept
Imagine a pizza cut into 5 equal slices. The fraction 2/5 represents taking 2 of those 5 slices. If we consider the whole pizza as 100%, then each slice represents 20% (100% / 5 slices = 20% per slice). Taking 2 slices would therefore be 2 slices * 20%/slice = 40%. This visual representation helps to solidify the understanding of the conversion.
The Significance of Understanding Fraction-Decimal-Percentage Conversions
The ability to seamlessly convert between fractions, decimals, and percentages is crucial for a variety of applications across numerous fields:
-
Everyday Life: Calculating discounts, tips, sales tax, and understanding interest rates all require this skill. For instance, a 40% discount on a $100 item means you save $40 (40% of $100).
-
Finance and Accounting: Analyzing financial statements, calculating profit margins, and understanding investment returns rely heavily on these conversions.
-
Science and Engineering: Many scientific and engineering calculations involve manipulating fractions, decimals, and percentages to express ratios, proportions, and probabilities.
-
Data Analysis: Interpreting data presented in different formats requires proficiency in these conversions to accurately analyze trends and make informed decisions.
Expanding on the Concept: Working with More Complex Fractions
The methods described above can be applied to convert any fraction into a percentage. For example, let's convert 3/8 to a percentage:
-
Convert to a decimal: 3 ÷ 8 = 0.375
-
Convert to a percentage: 0.375 x 100 = 37.5%
Therefore, 3/8 is equivalent to 37.5%.
Similarly, for more complex fractions with larger numbers, you can use a calculator or follow the same principles of division and multiplication to achieve the conversion. Remember to always divide the numerator by the denominator before multiplying by 100 to get the percentage.
Addressing Frequently Asked Questions (FAQs)
Q1: Can I convert a percentage back to a fraction?
Yes, absolutely! To convert a percentage to a fraction, divide the percentage by 100 and simplify the resulting fraction. For example, to convert 40% back to a fraction:
40% = 40/100 = 2/5 (after simplifying by dividing both numerator and denominator by 20).
Q2: What if the decimal resulting from the fraction division is a repeating decimal?
When you convert a fraction to a decimal and the result is a repeating decimal (e.g., 1/3 = 0.3333...), you can either round the decimal to a certain number of decimal places before converting it to a percentage, or you can express the percentage with a repeating decimal (e.g., 33.333...%). The level of precision required depends on the context of the problem.
Q3: Are there any shortcuts for converting certain common fractions to percentages?
Yes, memorizing some common fraction-percentage equivalents can be helpful:
- 1/2 = 50%
- 1/4 = 25%
- 3/4 = 75%
- 1/5 = 20%
- 2/5 = 40%
- 3/5 = 60%
- 4/5 = 80%
- 1/10 = 10%
Q4: Why is understanding percentages important in real-world scenarios?
Percentages provide a standardized and easily understandable way to compare and interpret proportions. Whether it's understanding discounts, interest rates, or statistical data, percentages make it simpler to grasp the relative magnitude of quantities.
Conclusion: Mastering Fraction-to-Percentage Conversions
Converting fractions to percentages is a fundamental mathematical skill with wide-ranging applications. By understanding the underlying concepts and employing the straightforward methods outlined in this article, you can confidently convert any fraction to its percentage equivalent. Practice is key to mastering this skill, so try converting different fractions to percentages to build your proficiency and confidence. Remember, this skill is not just about numbers; it's about understanding proportions and applying that understanding to various real-world scenarios. With consistent practice, you will develop a solid understanding of this essential concept and confidently navigate the world of fractions, decimals, and percentages.
Latest Posts
Latest Posts
-
How To Find The X Intercept Of A Logarithmic Function
Sep 11, 2025
-
System Of Equations With The Solution 4
Sep 11, 2025
-
3 4 Divided By 1 8 As A Fraction
Sep 11, 2025
-
How To Convert From Molecules To Atoms
Sep 11, 2025
-
Can Change In Entropy Be Negative
Sep 11, 2025
Related Post
Thank you for visiting our website which covers about What Percent Is Equivalent To 2/5 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.