3 4 Divided By 1 8 As A Fraction
faraar
Sep 11, 2025 · 5 min read
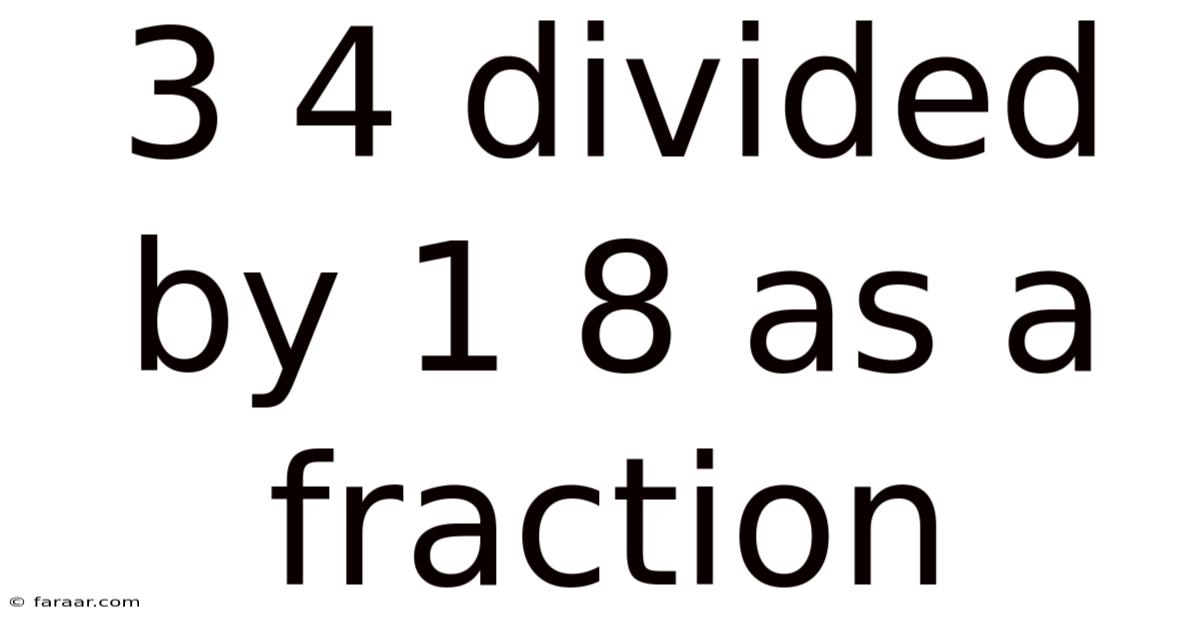
Table of Contents
Understanding 3 4/18 as a Fraction: A Comprehensive Guide
Dividing fractions and mixed numbers can seem daunting, but with a clear understanding of the underlying principles, it becomes a manageable and even enjoyable mathematical exercise. This article will thoroughly explore the division of 3 4/18, explaining the process step-by-step, delving into the underlying mathematical concepts, and addressing common questions and misconceptions. We will break down the problem into easily digestible parts, ensuring you gain not just the answer but a deeper understanding of fractional division.
Understanding Mixed Numbers and Improper Fractions
Before we tackle the division, let's refresh our understanding of mixed numbers and improper fractions. A mixed number combines a whole number and a fraction, like 3 4/18. An improper fraction, on the other hand, has a numerator (top number) larger than or equal to its denominator (bottom number). To divide mixed numbers, it's often easier to convert them into improper fractions.
To convert 3 4/18 to an improper fraction, we follow these steps:
- Multiply the whole number by the denominator: 3 * 18 = 54
- Add the numerator to the result: 54 + 4 = 58
- Keep the same denominator: The denominator remains 18.
Therefore, 3 4/18 is equivalent to the improper fraction 58/18.
Dividing Fractions: The Reciprocal Method
Dividing fractions involves a crucial concept: the reciprocal. The reciprocal of a fraction is simply the fraction flipped upside down. For example, the reciprocal of 2/3 is 3/2. To divide fractions, we replace the division sign with a multiplication sign and use the reciprocal of the second fraction.
Let's illustrate this with a simpler example: 1/2 ÷ 1/4.
- Find the reciprocal of the second fraction: The reciprocal of 1/4 is 4/1.
- Change division to multiplication: 1/2 ÷ 1/4 becomes 1/2 * 4/1.
- Multiply the numerators and the denominators: (1 * 4) / (2 * 1) = 4/2.
- Simplify the result: 4/2 simplifies to 2.
Therefore, 1/2 ÷ 1/4 = 2.
Solving 3 4/18 ÷ 1 8 as a Fraction: A Step-by-Step Approach
Now, let's apply this knowledge to our original problem: 3 4/18 ÷ 1 8.
Step 1: Convert Mixed Numbers to Improper Fractions
- As we established earlier, 3 4/18 converts to 58/18.
- 1 8 (which is 1 and 8/1) converts to (1*1 + 8)/1 = 9/1.
Step 2: Rewrite the Problem Using Improper Fractions
Our problem now becomes: 58/18 ÷ 9/1
Step 3: Find the Reciprocal of the Second Fraction
The reciprocal of 9/1 is 1/9.
Step 4: Change Division to Multiplication and Solve
58/18 ÷ 9/1 becomes 58/18 * 1/9
Multiply the numerators: 58 * 1 = 58 Multiply the denominators: 18 * 9 = 162
This gives us the improper fraction 58/162.
Step 5: Simplify the Fraction (Reduce to Lowest Terms)
To simplify 58/162, we need to find the greatest common divisor (GCD) of 58 and 162. The GCD of 58 and 162 is 2. Dividing both the numerator and the denominator by 2 gives us:
58/2 = 29 162/2 = 81
Therefore, the simplified fraction is 29/81.
Step 6: Final Answer
The solution to 3 4/18 ÷ 1 8 as a fraction is 29/81. This fraction is in its simplest form as 29 and 81 share no common factors other than 1.
Mathematical Explanation and Concepts
The process of dividing fractions relies on the fundamental principles of multiplicative inverses (reciprocals) and the commutative property of multiplication. When we multiply a fraction by its reciprocal, the result is always 1. This is crucial because division is essentially the inverse operation of multiplication. By using the reciprocal and changing division to multiplication, we’re effectively finding the number that, when multiplied by the divisor, equals the dividend.
The simplification process, reducing the fraction to its lowest terms, ensures that the answer is expressed in its most concise and accurate form. This involves finding the greatest common divisor (GCD) of the numerator and denominator and dividing both by this GCD. Finding the GCD can be done through various methods, such as prime factorization or the Euclidean algorithm.
Frequently Asked Questions (FAQ)
Q: Can I convert the final answer back to a mixed number?
A: While the question asked for a fractional answer, you can convert 29/81 back to a mixed number if needed. Since 29 is smaller than 81, the whole number part will be 0. The fractional part remains 29/81. Therefore, 29/81 as a mixed number is 0 29/81.
Q: What if I made a mistake in converting the mixed numbers to improper fractions?
A: Incorrect conversion of mixed numbers to improper fractions will lead to an incorrect final answer. Double-checking this step is crucial for accuracy.
Q: Are there other methods to solve this problem?
A: While the reciprocal method is efficient, you could also convert the mixed numbers to decimals, perform the division, and then convert the decimal back to a fraction. However, this method can sometimes lead to rounding errors, especially with non-terminating decimals. The method described above is generally preferred for its precision.
Q: Why is simplifying the fraction important?
A: Simplifying a fraction is important for several reasons: it makes the answer easier to understand and work with; it presents the answer in its most concise form; and it ensures that the answer is expressed in its most accurate representation. An unsimplified fraction can be more cumbersome and might create confusion in further calculations.
Conclusion
Dividing mixed numbers like 3 4/18 by 1 8 might initially seem complex, but breaking down the problem into smaller, manageable steps, as outlined above, clarifies the process. Mastering this skill involves understanding mixed numbers, improper fractions, reciprocals, and the principles of fraction multiplication and simplification. By applying the steps consistently and carefully checking your work, you can confidently tackle similar division problems and develop a strong foundation in fractional arithmetic. Remember, practice is key to mastering these concepts. Work through additional examples to solidify your understanding and build your confidence. With consistent effort, you'll find that fractional division becomes second nature.
Latest Posts
Latest Posts
-
5 5 5 5 5 Answer
Sep 11, 2025
-
An Organelle That Functions In The Synthesis Of Proteins
Sep 11, 2025
-
Is Ch3 An Electron Withdrawing Group
Sep 11, 2025
-
When To Use Por Vs Para In Spanish
Sep 11, 2025
-
A Voltmeter Has An Internal Resistance Of 1000 Ohm
Sep 11, 2025
Related Post
Thank you for visiting our website which covers about 3 4 Divided By 1 8 As A Fraction . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.