What Is The Solution To 4log4 X 8 4 2
faraar
Sep 21, 2025 · 5 min read
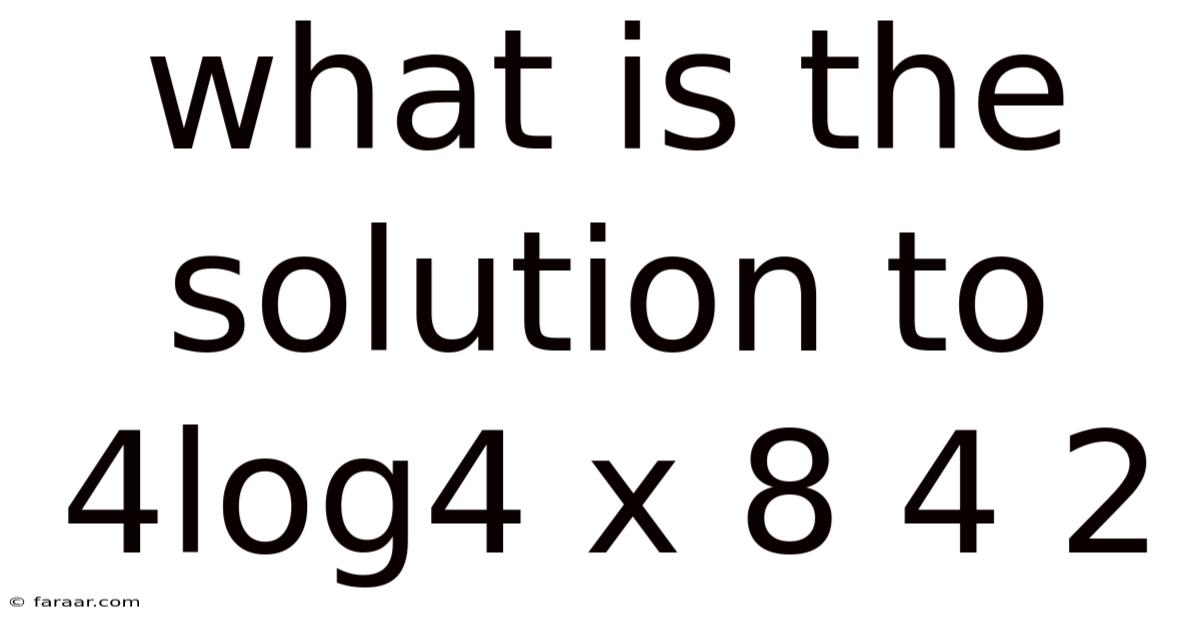
Table of Contents
Decoding the Logarithmic Equation: Solving 4log₄(x) = 8⁴ ÷ 2
This article delves into the solution of the logarithmic equation 4log₄(x) = 8⁴ ÷ 2. We'll break down the problem step-by-step, explaining the underlying principles of logarithms and exponentials, and providing a clear, concise solution. Understanding this equation requires familiarity with logarithmic properties and the order of operations (PEMDAS/BODMAS). This detailed explanation will not only provide the answer but also enhance your understanding of logarithmic functions, making you confident in tackling similar problems.
Understanding the Components: Logarithms and Exponents
Before tackling the equation, let's refresh our understanding of logarithms and exponents. These two mathematical concepts are inversely related.
-
Exponents: An exponent indicates how many times a base number is multiplied by itself. For example, 2³ = 2 * 2 * 2 = 8. Here, 2 is the base, and 3 is the exponent.
-
Logarithms: A logarithm is the inverse operation of exponentiation. The logarithmic expression logₐ(b) = c means that a raised to the power of c equals b (aᶜ = b). In simpler terms, it asks: "To what power must we raise 'a' to get 'b'?" The 'a' is called the base of the logarithm.
In our equation, we have a logarithm with base 4: log₄(x). This means we're looking for the power to which we must raise 4 to obtain x.
Step-by-Step Solution of 4log₄(x) = 8⁴ ÷ 2
Let's solve the equation systematically, following the order of operations:
1. Simplify the Right-Hand Side (RHS):
First, we simplify the right-hand side of the equation: 8⁴ ÷ 2.
8⁴ = 8 * 8 * 8 * 8 = 4096
Therefore, 8⁴ ÷ 2 = 4096 ÷ 2 = 2048.
Our equation now becomes: 4log₄(x) = 2048
2. Isolate the Logarithmic Term:
Next, we isolate the logarithmic term, log₄(x), by dividing both sides of the equation by 4:
(4log₄(x)) / 4 = 2048 / 4
This simplifies to:
log₄(x) = 512
3. Convert the Logarithmic Equation to Exponential Form:
Remember the definition of a logarithm: logₐ(b) = c is equivalent to aᶜ = b. Applying this to our equation (log₄(x) = 512), we get:
4⁵¹² = x
4. Calculate the Value of x:
While calculating 4⁵¹² directly is computationally intensive, we can use the properties of exponents to simplify. We know that 4 = 2². Therefore, we can rewrite the equation as:
(2²)⁵¹² = x
Using the power of a power rule ((aᵇ)ᶜ = aᵇᶜ), we get:
2⁽²*⁵¹²⁾ = x
2¹⁰²⁴ = x
Therefore, the value of x is 2¹⁰²⁴. This is an extremely large number and usually left in exponential form for practical purposes.
A Deeper Dive into Logarithmic Properties
Understanding the properties of logarithms is crucial for solving more complex logarithmic equations. Here are some key properties:
- Product Rule: logₐ(mn) = logₐ(m) + logₐ(n)
- Quotient Rule: logₐ(m/n) = logₐ(m) – logₐ(n)
- Power Rule: logₐ(mⁿ) = nlogₐ(m)
- Change of Base Formula: logₐ(b) = logₓ(b) / logₓ(a) (where x is any valid base)
These properties are incredibly useful for manipulating and simplifying logarithmic expressions. For instance, the power rule was implicitly used in step 2 of our solution when we divided both sides of the equation by 4. This is because dividing by 4 is the same as multiplying by ¼, which can be written as 4⁻¹. Therefore, we could have also written:
4¹log₄(x) = 2048
Applying the power rule in reverse we would obtain:
log₄(x⁴) = 2048
Which could then be converted into exponential form and simplified in a different way.
Practical Applications of Logarithms
Logarithms have widespread applications in various fields:
- Science: Used to measure earthquake intensity (Richter scale), sound intensity (decibels), and acidity (pH scale).
- Engineering: Essential in calculations involving exponential growth and decay (e.g., radioactive decay, population growth).
- Finance: Used in compound interest calculations and modeling financial growth.
- Computer Science: Used in algorithms and data analysis.
Frequently Asked Questions (FAQ)
Q1: Can I use a calculator to solve 4⁵¹²?
A1: Most standard calculators will struggle with a number this large. Scientific calculators or specialized software may handle it, but the result would likely be expressed in scientific notation due to the magnitude of the number. Leaving the answer as 2¹⁰²⁴ is more practical and accurate in most contexts.
Q2: What if the base of the logarithm was different?
A2: The process remains similar. You would still follow the order of operations, isolate the logarithmic term, and then convert the equation to exponential form using the appropriate base. The change of base formula would be useful if you need to convert to a more convenient base for calculation.
Q3: Are there other ways to solve this equation?
A3: While the method outlined above is the most straightforward, alternative approaches involving more advanced logarithmic manipulations might exist, but they would likely add complexity without significant advantage in this specific case.
Conclusion
Solving the equation 4log₄(x) = 8⁴ ÷ 2 requires a solid understanding of logarithms and exponents, along with a methodical approach to simplification. The solution, x = 2¹⁰²⁴, highlights the power of logarithmic manipulation and the importance of using the properties of logarithms and exponents effectively. This equation serves as an excellent exercise to strengthen your problem-solving skills in mathematics and deepen your understanding of logarithmic functions. Remember that practice is key to mastering these concepts, so try solving similar equations to further solidify your knowledge. By understanding the fundamentals and applying the steps outlined above, you can confidently tackle a wide range of logarithmic equations.
Latest Posts
Latest Posts
-
Reading And Writing Tutoring Near Me
Sep 21, 2025
-
How Do You Find The Amplitude Of A Tangent Graph
Sep 21, 2025
-
How Many Valence Electrons Are Found In Phosphorus
Sep 21, 2025
-
How Far Is 40 Miles In Minutes Driving
Sep 21, 2025
-
How To Know If Two Functions Are Inverses
Sep 21, 2025
Related Post
Thank you for visiting our website which covers about What Is The Solution To 4log4 X 8 4 2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.