8 Less Than 3 Times X
faraar
Sep 16, 2025 · 5 min read
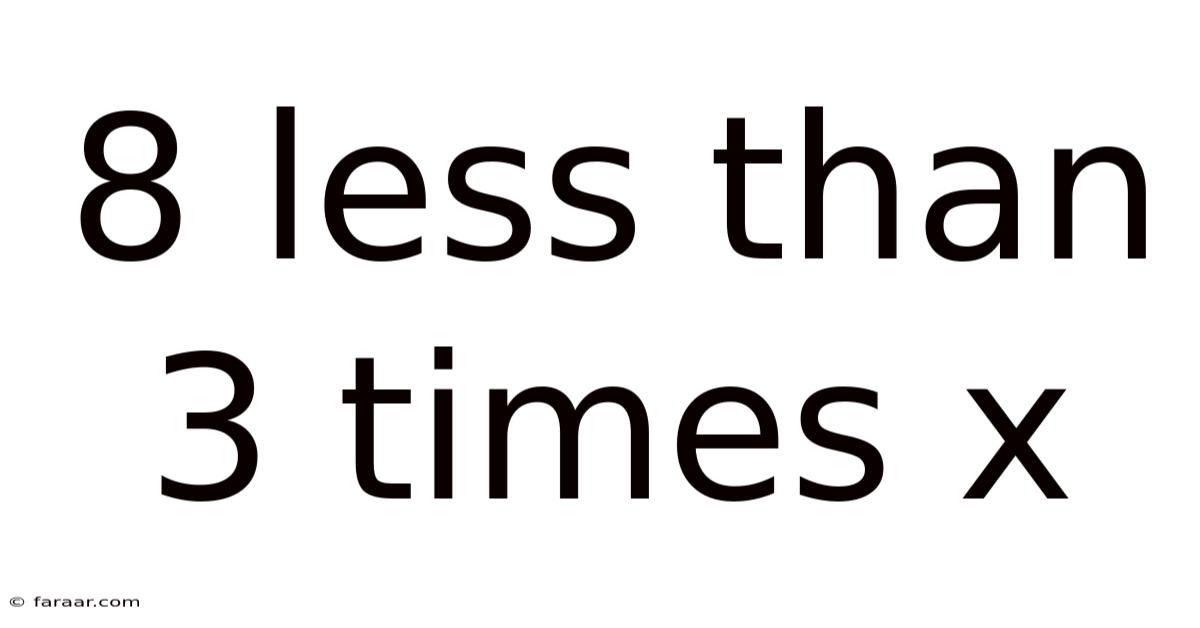
Table of Contents
Decoding "8 Less Than 3 Times x": A Deep Dive into Algebraic Expressions
This article explores the algebraic expression "8 less than 3 times x," breaking down its meaning, explaining how to represent it mathematically, and demonstrating its application in various contexts. Understanding this seemingly simple phrase is foundational to mastering algebra and its practical applications in various fields, from simple calculations to complex problem-solving. We'll delve into its structure, explore different ways to represent it, and provide examples to solidify your understanding. This comprehensive guide will cover everything you need to know about this core algebraic concept.
Understanding the Phrase: "8 Less Than 3 Times x"
At first glance, "8 less than 3 times x" might seem confusing. However, by breaking it down into its constituent parts, the meaning becomes clear. Let's dissect the phrase:
-
"3 times x": This part is straightforward. It means 3 multiplied by x, which can be written as 3x or 3 * x. 'x' here represents a variable, meaning it can take on various numerical values.
-
"8 less than": This phrase indicates subtraction. We are taking 8 away from something.
Combining these parts, "8 less than 3 times x" means we start with "3 times x" (3x) and then subtract 8 from it.
Representing the Phrase Mathematically
The phrase "8 less than 3 times x" translates directly into the algebraic expression: 3x - 8. This is the standard and most concise way to represent this relationship. It's crucial to understand the order of operations; subtraction is performed after the multiplication.
We could also represent it in a slightly less concise, but equally valid way: 3 * x - 8. This emphasizes the multiplication operation, which can be beneficial for beginners. However, as your algebraic skills improve, the shorter form (3x - 8) becomes the preferred method.
Exploring Different Scenarios and Applications
Let's explore how this expression works with different values of x. Imagine ‘x’ representing various real-world quantities:
-
Scenario 1: x represents the number of apples. If you have 'x' apples, and you triple the amount (3x), and then give away 8 apples (3x - 8), the remaining number of apples is represented by the expression 3x - 8. If x = 5 (you initially have 5 apples), then 3x - 8 = 3(5) - 8 = 15 - 8 = 7. You would have 7 apples left.
-
Scenario 2: x represents the price of an item. If an item costs 'x' dollars and you buy three of them (3x), then receive an $8 discount (3x - 8), the total cost after the discount is represented by 3x - 8. If x = 10 (each item costs $10), then 3x - 8 = 3(10) - 8 = 30 - 8 = $22. The total cost would be $22.
-
Scenario 3: x represents hours worked. If you earn 'x' dollars per hour and work three hours (3x), but have $8 deducted for taxes or other fees (3x - 8), your net earnings are 3x - 8. If x = 15 (you earn $15 per hour), then 3x - 8 = 3(15) - 8 = 45 - 8 = $37. Your net pay would be $37.
Solving Equations Involving "3x - 8"
The expression "3x - 8" often forms part of a larger algebraic equation. Let's consider a few examples:
- Example 1: 3x - 8 = 10
To solve for x, we need to isolate x. We do this by following these steps:
- Add 8 to both sides: 3x - 8 + 8 = 10 + 8 => 3x = 18
- Divide both sides by 3: 3x / 3 = 18 / 3 => x = 6
Therefore, the solution to the equation 3x - 8 = 10 is x = 6.
- Example 2: 2(3x - 8) = 20
This equation involves the distributive property. First, we distribute the 2:
- Distribute: 6x - 16 = 20
- Add 16 to both sides: 6x - 16 + 16 = 20 + 16 => 6x = 36
- Divide both sides by 6: 6x / 6 = 36 / 6 => x = 6
Again, x = 6 is the solution.
- Example 3: 3x - 8 > 10 (Inequality)
This is an inequality, not an equation. The steps are similar, but the solution will be a range of values:
- Add 8 to both sides: 3x > 18
- Divide both sides by 3: x > 6
The solution to this inequality is x > 6, meaning x can be any value greater than 6.
The Importance of Order of Operations (PEMDAS/BODMAS)
Remember the order of operations, often represented by the acronyms PEMDAS (Parentheses, Exponents, Multiplication and Division, Addition and Subtraction) or BODMAS (Brackets, Orders, Division and Multiplication, Addition and Subtraction). In the expression 3x - 8, multiplication (3x) must be performed before subtraction (-8). Ignoring this order will lead to incorrect results.
Practical Applications Beyond Simple Arithmetic
The ability to understand and manipulate algebraic expressions like "3x - 8" extends far beyond simple arithmetic problems. It's a fundamental skill used in:
-
Physics: Calculating distances, velocities, accelerations, and forces often involves algebraic expressions.
-
Engineering: Designing structures, circuits, and systems requires extensive use of algebraic equations.
-
Finance: Calculating interest, profits, losses, and investments rely heavily on algebraic manipulations.
-
Computer Science: Programming and algorithms frequently use algebraic logic and expressions.
-
Data Analysis: Statistical modeling and data interpretation often involve algebraic equations.
Frequently Asked Questions (FAQ)
Q: What if the phrase was "8 less than twice x"?
A: That would translate to 2x - 8. The coefficient of x simply changes.
Q: Can 'x' be a negative number?
A: Yes, absolutely. 'x' can represent any real number, positive, negative, or zero.
Q: How do I graph the expression 3x - 8?
A: You can graph it as a linear equation. It will be a straight line with a slope of 3 and a y-intercept of -8.
Q: What if I have a more complex expression involving 3x - 8?
A: The same principles apply. Simplify the expression according to the order of operations, and then solve for x (or manipulate it as needed depending on the problem).
Conclusion
Understanding the algebraic expression "8 less than 3 times x" and its representation as 3x - 8 is a crucial step in mastering fundamental algebraic concepts. This seemingly simple phrase lays the groundwork for solving more complex equations, inequalities, and real-world problems. Through careful understanding of the order of operations and practice solving various equations, you can build a strong foundation in algebra and its widespread applications. Remember, consistent practice and attention to detail are key to achieving proficiency. By breaking down complex problems into their smaller, manageable parts, you can unlock a deeper understanding of the power of algebra.
Latest Posts
Latest Posts
-
Tutoring For 4 Year Olds Near Me
Sep 16, 2025
-
What Is 36 Divided By 2
Sep 16, 2025
-
As Long As Vs So Long As
Sep 16, 2025
-
How Long Should You Study For Mcat
Sep 16, 2025
-
Sum Of Exterior Angles Of A Octagon
Sep 16, 2025
Related Post
Thank you for visiting our website which covers about 8 Less Than 3 Times X . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.