What Is 5/3 As A Percent
faraar
Sep 22, 2025 · 5 min read
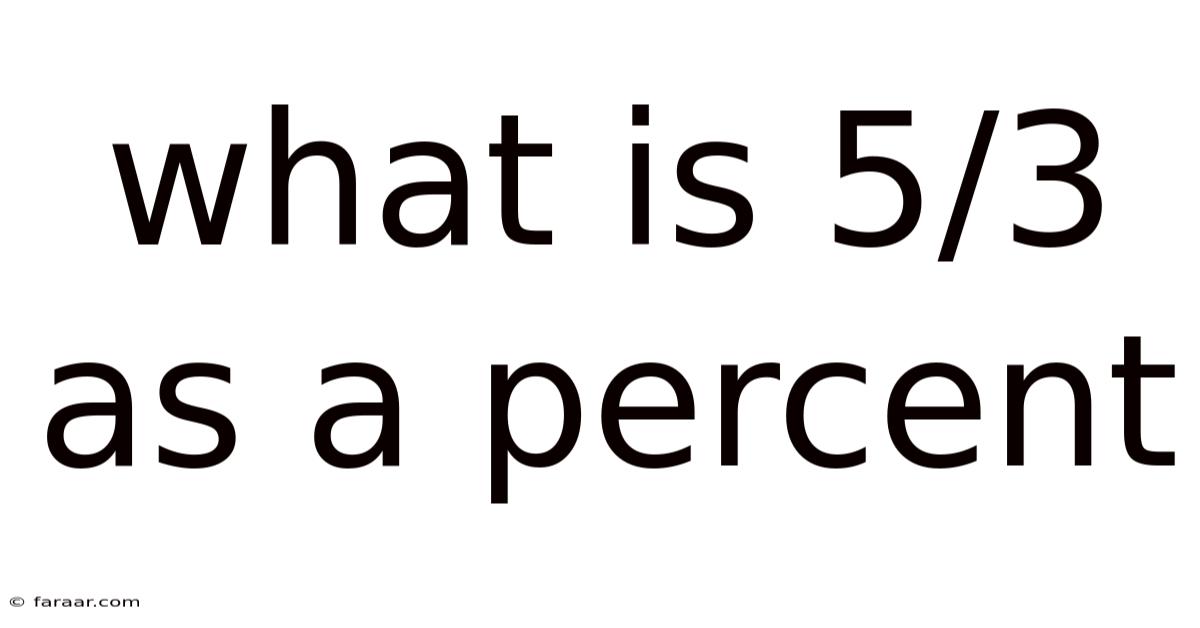
Table of Contents
What is 5/3 as a Percent? A Comprehensive Guide to Fraction-to-Percentage Conversion
Understanding how to convert fractions to percentages is a fundamental skill in mathematics with applications spanning various fields, from finance and statistics to everyday calculations. This comprehensive guide will not only answer the question "What is 5/3 as a percent?" but also provide a thorough understanding of the underlying principles and methods involved in fraction-to-percentage conversions. We'll explore different approaches, address common misconceptions, and equip you with the knowledge to tackle similar problems confidently.
Understanding Fractions and Percentages
Before diving into the conversion process, let's briefly review the concepts of fractions and percentages.
A fraction represents a part of a whole. It consists of a numerator (the top number) and a denominator (the bottom number). The numerator indicates how many parts we have, and the denominator indicates how many equal parts the whole is divided into. For example, in the fraction 5/3, 5 is the numerator and 3 is the denominator. This fraction represents five-thirds, meaning we have five parts of a whole that's been divided into three equal parts. Note that 5/3 is an improper fraction because the numerator is larger than the denominator.
A percentage, denoted by the symbol %, represents a fraction of 100. It expresses a proportion out of a hundred. For instance, 25% means 25 out of 100, which can be written as the fraction 25/100 or the decimal 0.25.
Method 1: Converting the Fraction to a Decimal, Then to a Percentage
This is arguably the most straightforward method for converting fractions to percentages. It involves two steps:
Step 1: Convert the Fraction to a Decimal
To convert a fraction to a decimal, we simply divide the numerator by the denominator. In our case:
5 ÷ 3 = 1.666...
The result is a repeating decimal (1.666...). We can round this to a certain number of decimal places for practical purposes. For example, rounding to two decimal places, we get 1.67.
Step 2: Convert the Decimal to a Percentage
To convert a decimal to a percentage, we multiply the decimal by 100 and add the "%" symbol. Using our rounded decimal value of 1.67:
1.67 × 100 = 167%
Therefore, 5/3 as a percent is approximately 167%. The "..." indicates that the decimal continues infinitely, implying that 167% is an approximation.
Method 2: Finding an Equivalent Fraction with a Denominator of 100
This method involves finding an equivalent fraction where the denominator is 100. This equivalent fraction directly represents the percentage. However, this method isn't always practical, particularly with fractions that don't easily simplify to a denominator of 100.
To illustrate, let's try this method. We want to find a number that, when multiplied by 3 (the denominator), results in 100. This would involve solving the equation 3x = 100, which gives x = 100/3. This is not a whole number, making this approach less efficient in this specific instance. While theoretically possible, the resulting calculation will be more complex than the decimal-to-percentage method.
Method 3: Understanding the Concept of Improper Fractions and Percentages Greater Than 100%
The result, 167%, is a percentage greater than 100%. This is perfectly valid and signifies that the fraction 5/3 represents more than one whole. Imagine you have three equal slices of pizza, and you have five of these slices. This means you have more than one whole pizza (one whole pizza would be 3/3). The extra two slices represent the amount exceeding 100%.
Addressing Common Misconceptions
A common mistake is to directly multiply the numerator by 100 and then divide by the denominator. This is incorrect. The correct approach is to first convert the fraction to a decimal before multiplying by 100.
Another misconception involves interpreting fractions as percentages without proper conversion. While some fractions might intuitively suggest a percentage (e.g., 1/2 = 50%), this is not a general rule and applying this without calculation is unreliable.
Practical Applications
The ability to convert fractions to percentages is crucial in many real-world situations:
- Finance: Calculating interest rates, profit margins, and discounts often involves converting fractions to percentages.
- Statistics: Representing data proportions and probabilities often uses percentages derived from fractions.
- Everyday Life: Calculating tips, sale prices, and portion sizes often requires converting fractions to percentages.
Frequently Asked Questions (FAQ)
Q: Can all fractions be converted to percentages?
A: Yes, all fractions, whether proper or improper, can be converted to percentages.
Q: What if the decimal resulting from the fraction is non-terminating and non-repeating?
A: In such cases, you'll need to round the decimal to a suitable number of decimal places for practical purposes.
Q: Is it always necessary to round the percentage?
A: Rounding is often necessary for practicality, especially when dealing with non-terminating decimals. However, you can retain the exact percentage representation using the repeating decimal format (e.g., 166.666...).
Q: How do I convert a mixed number (e.g., 1 2/3) to a percentage?
A: First, convert the mixed number to an improper fraction (in this case, 5/3). Then, follow the methods described above to convert the improper fraction to a percentage.
Q: Are there other methods to convert fractions to percentages?
A: While the methods outlined above are the most common and straightforward, more advanced mathematical techniques exist but are generally not necessary for basic conversions.
Conclusion
Converting fractions to percentages is a fundamental mathematical skill with widespread applications. By understanding the underlying principles and employing the methods discussed in this guide, you can confidently convert any fraction to a percentage. Remember that the key steps involve converting the fraction to a decimal and then multiplying by 100 to obtain the percentage. This guide has not only answered the specific question of what 5/3 is as a percent (approximately 167%) but also provided you with the broader tools to tackle various fraction-to-percentage conversion problems accurately and efficiently. Understanding the concept of improper fractions and percentages exceeding 100% is crucial for complete comprehension of this mathematical concept.
Latest Posts
Latest Posts
-
What Is The Purpose Of A Topic Sentence
Sep 22, 2025
-
Which Is The Correct Graph Of The Inequality Y 2x 1
Sep 22, 2025
-
Write The Balanced Ka And Kb Reactions For Hso3
Sep 22, 2025
-
How To Find Height Of Pyramid
Sep 22, 2025
-
Which Of The Lines Below Has A Slope Of Zero
Sep 22, 2025
Related Post
Thank you for visiting our website which covers about What Is 5/3 As A Percent . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.