What Is 3 4 1 3 As A Fraction
faraar
Sep 23, 2025 · 6 min read
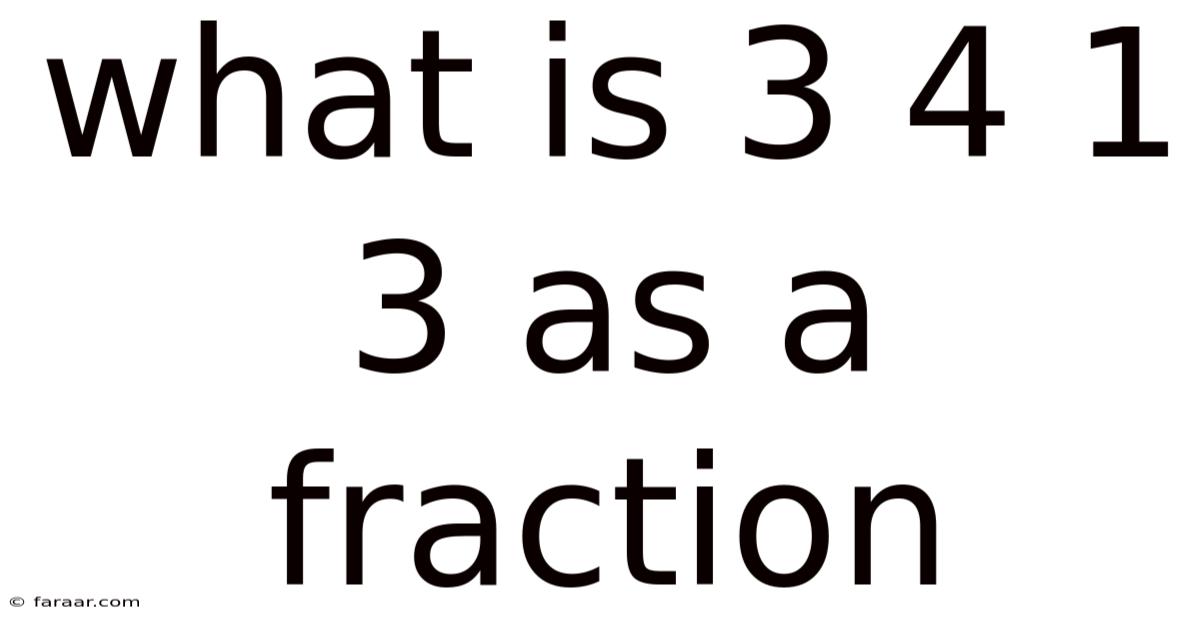
Table of Contents
Decoding 3 4 1 3: Unveiling the Fraction Behind the Sequence
Understanding the representation of numbers is a fundamental skill in mathematics. This article delves into the intriguing question: what is 3 4 1 3 as a fraction? At first glance, "3 4 1 3" might seem like a random sequence of numbers. However, depending on the context, it could represent a mixed number, a decimal number, or even a more complex mathematical expression. We will explore various interpretations and demonstrate how to convert these representations into their fractional equivalents. This exploration will provide a solid understanding of fundamental mathematical concepts, including mixed numbers, improper fractions, and decimal-to-fraction conversions.
Understanding the Potential Interpretations of "3 4 1 3"
The ambiguity of "3 4 1 3" stems from the lack of explicit operators or separators. We need to consider different scenarios:
-
Scenario 1: A Mixed Number: The most straightforward interpretation is to assume "3 4 1 3" represents a mixed number. Mixed numbers combine a whole number and a proper fraction. However, the sequence "3 4 1 3" doesn't immediately fit the standard format of a mixed number (Whole Number + Numerator/Denominator). To interpret it as a mixed number, we'd need additional information or context. One possibility is that it might be a shorthand notation, needing clarification. For instance, it might be miswritten and intended to be something like 3 ⁴⁄₁₃ (three and four thirteenths).
-
Scenario 2: Concatenated Decimal: We could interpret "3 4 1 3" as a concatenated decimal number, representing 3413. In this case, the challenge becomes converting the decimal number 3413 into a fraction.
-
Scenario 3: Part of a Larger Expression: The sequence might be a part of a larger mathematical expression, not standing alone as a numerical value. It could be an element within a sequence, matrix, or a more complex equation. Without knowing the complete expression, we can't determine its fractional representation.
Converting Decimal Numbers to Fractions: The Core Method
Let's assume "3 4 1 3" is representing the decimal number 3413. To convert a decimal number into a fraction, we follow a systematic approach:
-
Write the decimal number as the numerator: Place the decimal number (3413) over 1 as the denominator. This creates an improper fraction: 3413/1
-
Identify the place value of the last digit: In this case, the last digit '3' is in the ones place.
-
Simplify the fraction (if possible): Since 3413 is not evenly divisible by any common factors other than 1, the fraction 3413/1 is already in its simplest form. Therefore, the fraction representation of the decimal 3413 is 3413/1.
Working with Mixed Numbers: A Detailed Guide
Let's consider the possibility that "3 4 1 3" was intended as a mixed number, perhaps a shorthand notation requiring interpretation. For the sake of illustration, let's assume it was meant to represent 3 ⁴⁄₁₃ (three and four thirteenths). Here’s how to convert such a mixed number into an improper fraction:
-
Multiply the whole number by the denominator: Multiply the whole number (3) by the denominator of the fraction (13): 3 * 13 = 39
-
Add the numerator: Add the result from step 1 to the numerator of the fraction (4): 39 + 4 = 43
-
Keep the same denominator: The denominator remains the same (13).
-
Form the improper fraction: The improper fraction is 43/13.
Therefore, the mixed number 3 ⁴⁄₁₃ is equivalent to the improper fraction 43/13.
Expanding on Fraction Conversions: A Broader Perspective
The examples above highlight the crucial steps in converting both decimal numbers and mixed numbers into fractions. Let's further expand our understanding with additional scenarios and concepts:
-
Converting Proper Fractions to Decimals: To convert a proper fraction to a decimal, divide the numerator by the denominator. For example, the fraction ⁴⁄₁₃ would be calculated as 4 ÷ 13 ≈ 0.3077.
-
Converting Improper Fractions to Mixed Numbers: If we have an improper fraction (where the numerator is larger than the denominator), we can convert it to a mixed number by dividing the numerator by the denominator. The quotient becomes the whole number, and the remainder becomes the numerator of the fraction, retaining the original denominator. For example, let's convert 43/13:
- 43 ÷ 13 = 3 with a remainder of 4
- This gives us the mixed number 3 ⁴⁄₁₃.
-
Simplifying Fractions: It's important to simplify fractions to their lowest terms by finding the greatest common divisor (GCD) of the numerator and the denominator and dividing both by the GCD. For example, the fraction 12/18 can be simplified to 2/3 because the GCD of 12 and 18 is 6.
-
Equivalent Fractions: Equivalent fractions represent the same value, even though they have different numerators and denominators. You obtain equivalent fractions by multiplying or dividing both the numerator and the denominator by the same non-zero number. For example, 1/2, 2/4, and 3/6 are all equivalent fractions.
Addressing Potential Misinterpretations and FAQs
Given the ambiguity of the initial sequence "3 4 1 3," let's address some common questions and potential misinterpretations:
Q: What if "3 4 1 3" represents a different mathematical concept?
A: Without further context or clarifying information, it's difficult to definitively state what "3 4 1 3" might represent beyond the interpretations we've discussed. It could be a code, a shorthand notation specific to a particular field, or part of a more intricate mathematical equation.
Q: Could it represent a ratio?
A: While "3 4 1 3" could be interpreted as a ratio (3:4:1:3), this interpretation is different from a fraction. Ratios compare quantities, whereas fractions represent parts of a whole. Converting a ratio directly to a single fraction isn't always straightforward.
Q: Are there other ways to interpret this sequence?
A: Yes, depending on the context, it could signify different things altogether. For instance, in a programming context, it might be an array or a list. Without specific instructions or a problem statement, alternative interpretations are possible but difficult to confirm.
Conclusion: The Importance of Context and Clarity
The question, "What is 3 4 1 3 as a fraction?" highlights the significance of clear notation and contextual understanding in mathematics. The sequence itself is ambiguous. To accurately convert "3 4 1 3" into a fraction, additional information is necessary. We explored several possible interpretations, demonstrating the conversion process for decimal numbers and mixed numbers into their fractional equivalents. Mastering these conversion methods forms a strong foundation for more advanced mathematical concepts and problem-solving. Remember that precise notation and a clear understanding of the context are crucial for accurate mathematical interpretation. If faced with a similar ambiguous sequence, seek clarification to avoid misinterpretations and ensure accurate calculations.
Latest Posts
Latest Posts
-
What Is 23 25 As A Percentage
Sep 23, 2025
-
Are Vertical Asymptotes In The Numerator Or Denominator
Sep 23, 2025
-
How To Write 80 As A Fraction
Sep 23, 2025
-
When Solutions Of Nacl And Agno3 Are Mixed
Sep 23, 2025
-
When Is The Particle At Rest
Sep 23, 2025
Related Post
Thank you for visiting our website which covers about What Is 3 4 1 3 As A Fraction . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.