What Is 23/25 As A Percentage
faraar
Sep 23, 2025 · 6 min read
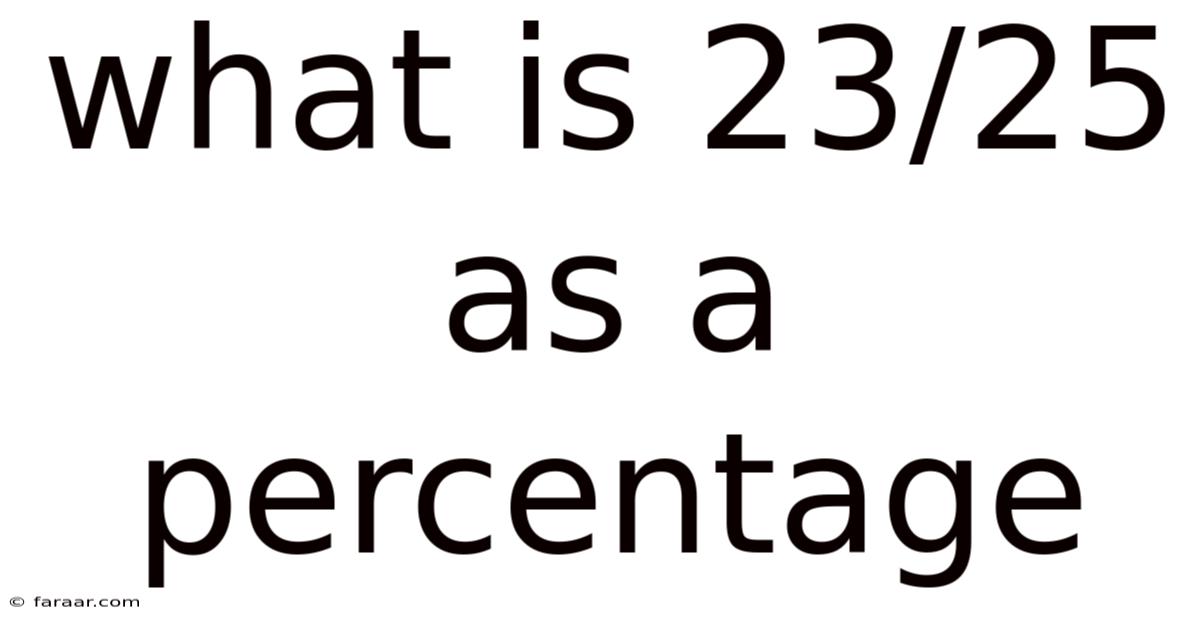
Table of Contents
What is 23/25 as a Percentage? A Comprehensive Guide to Fraction-to-Percentage Conversion
Converting fractions to percentages is a fundamental skill in mathematics with wide-ranging applications in everyday life, from calculating discounts and grades to understanding statistical data and financial reports. This comprehensive guide will not only answer the question "What is 23/25 as a percentage?" but also delve into the underlying principles, provide multiple methods for solving similar problems, and address frequently asked questions. Understanding this process empowers you to confidently tackle various percentage calculations.
Understanding Fractions and Percentages
Before diving into the conversion, let's clarify the concepts involved. A fraction represents a part of a whole. In the fraction 23/25, 23 is the numerator (the part) and 25 is the denominator (the whole). A percentage, denoted by the symbol %, represents a fraction of 100. Essentially, a percentage expresses a proportion out of 100. Therefore, converting a fraction to a percentage means finding the equivalent fraction with a denominator of 100.
Method 1: Direct Conversion Using Proportions
The most straightforward method to convert 23/25 to a percentage involves setting up a proportion. We want to find the percentage x such that:
23/25 = x/100
To solve for x, we cross-multiply:
23 * 100 = 25 * x
2300 = 25x
Now, divide both sides by 25:
x = 2300 / 25
x = 92
Therefore, 23/25 is equal to 92%.
This method highlights the core concept of percentages – expressing a fraction as a part of 100. It's a fundamental approach applicable to any fraction-to-percentage conversion.
Method 2: Converting the Fraction to a Decimal
Another common method involves first converting the fraction to a decimal and then multiplying by 100. To convert 23/25 to a decimal, we perform the division:
23 ÷ 25 = 0.92
Now, multiply the decimal by 100 to express it as a percentage:
0.92 * 100 = 92%
This method is particularly useful when working with fractions that are easily converted to decimals, especially those with denominators that are powers of 10 (10, 100, 1000, etc.). It offers a simple and efficient alternative to the proportion method.
Method 3: Simplifying the Fraction (if possible)
Sometimes, simplifying the fraction before conversion can make the calculation easier. However, in this case, 23 and 25 share no common factors other than 1, so simplification isn't possible. But let's consider an example where simplification is beneficial. Suppose we want to convert 15/25 to a percentage. We can simplify 15/25 by dividing both the numerator and the denominator by their greatest common divisor, which is 5:
15/25 = (15 ÷ 5) / (25 ÷ 5) = 3/5
Now, we can use either of the previous methods to convert 3/5 to a percentage:
- Method 1 (Proportion): 3/5 = x/100 => 300 = 5x => x = 60 => 60%
- Method 2 (Decimal): 3 ÷ 5 = 0.6 => 0.6 * 100 = 60%
This demonstrates how simplification can streamline the conversion process, making it less computationally intensive.
Understanding the Significance of 92%
The result, 92%, signifies that 23 represents 92 parts out of 100 equal parts of the whole. This percentage can be applied in diverse scenarios. For instance:
- Academic Performance: If a student answered 23 out of 25 questions correctly on a test, their score is 92%.
- Sales Target: If a sales representative achieved 23 out of 25 sales targets, their achievement rate is 92%.
- Project Completion: If 23 out of 25 project milestones are completed, the project is 92% complete.
The 92% represents a high level of achievement or completion, indicating strong performance or progress.
Expanding on Fraction-to-Percentage Conversions: Addressing Different Scenarios
The methods described above are applicable to converting any fraction to a percentage. Let's explore some additional scenarios:
-
Improper Fractions: Improper fractions (where the numerator is greater than the denominator) will result in percentages greater than 100%. For example, 27/25 converted to a percentage is: (27/25) * 100 = 108%. This indicates that the part exceeds the whole, which can occur in contexts like exceeding targets or growth beyond the expected.
-
Mixed Numbers: Mixed numbers (a whole number and a fraction) need to be converted to an improper fraction before applying the conversion methods. For instance, consider 2 1/4. This converts to 9/4. Using the proportion method: (9/4) = x/100 => 900 = 4x => x = 225. Therefore, 2 1/4 is 225%.
-
Decimals in Fractions: Fractions containing decimals in either the numerator or denominator require careful handling. For example, to convert 2.5/5 to a percentage, first simplify the fraction to 0.5 (or 1/2) then convert the decimal to percentage, giving us 50%.
-
Recurring Decimals: When dividing the numerator by the denominator results in a recurring decimal, you'll need to round the decimal to a suitable number of decimal places before multiplying by 100. For example, 1/3 gives us 0.3333... Rounding to two decimal places gives us 0.33, and multiplying by 100 yields 33%. This rounding introduces a slight margin of error but is often acceptable in practical applications.
Frequently Asked Questions (FAQ)
Q1: Why is converting fractions to percentages useful?
A1: Percentages provide a standardized and easily understandable way to compare proportions. They're widely used in various fields to represent data, track progress, and make comparisons more intuitive.
Q2: Can I use a calculator to convert fractions to percentages?
A2: Yes, most calculators have a percentage function or can perform the necessary divisions and multiplications. Simply divide the numerator by the denominator and then multiply the result by 100.
Q3: What if the denominator of the fraction is zero?
A3: A fraction with a denominator of zero is undefined. Division by zero is not mathematically permissible.
Q4: Are there any online tools or calculators to assist with this conversion?
A4: While many online tools and calculators exist for fraction-to-percentage conversion, they are beyond the scope of this self-contained guide.
Q5: How do I express percentages as fractions?
A5: To convert a percentage to a fraction, divide the percentage by 100 and simplify the resulting fraction. For example, 75% becomes 75/100, which simplifies to 3/4.
Conclusion: Mastering Fraction-to-Percentage Conversion
Converting fractions to percentages is a valuable skill applicable across various disciplines. By understanding the underlying principles and applying the methods outlined in this guide, you can confidently tackle such conversions. Whether you use the direct proportion method, the decimal conversion method, or a combination of both, remember that the goal is to express the fraction as an equivalent proportion out of 100. This understanding allows you to interpret percentages effectively and apply them to diverse real-world situations. Remember that practice is key to mastering this skill, so try converting various fractions to percentages to solidify your understanding. You'll soon find yourself proficiently navigating the world of fractions and percentages.
Latest Posts
Latest Posts
-
Write A Number With Digit 8 In The Tens Place
Sep 24, 2025
-
Triangle Abc Is Similar To Triangle D E F
Sep 24, 2025
-
Which Of The Following Is A Limited Resource
Sep 24, 2025
-
How Many Combinations With 2 Dice
Sep 24, 2025
-
Which Prism Has The Greatest Volume
Sep 24, 2025
Related Post
Thank you for visiting our website which covers about What Is 23/25 As A Percentage . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.