What Is 3/4 + 1 1/2
faraar
Aug 27, 2025 · 6 min read
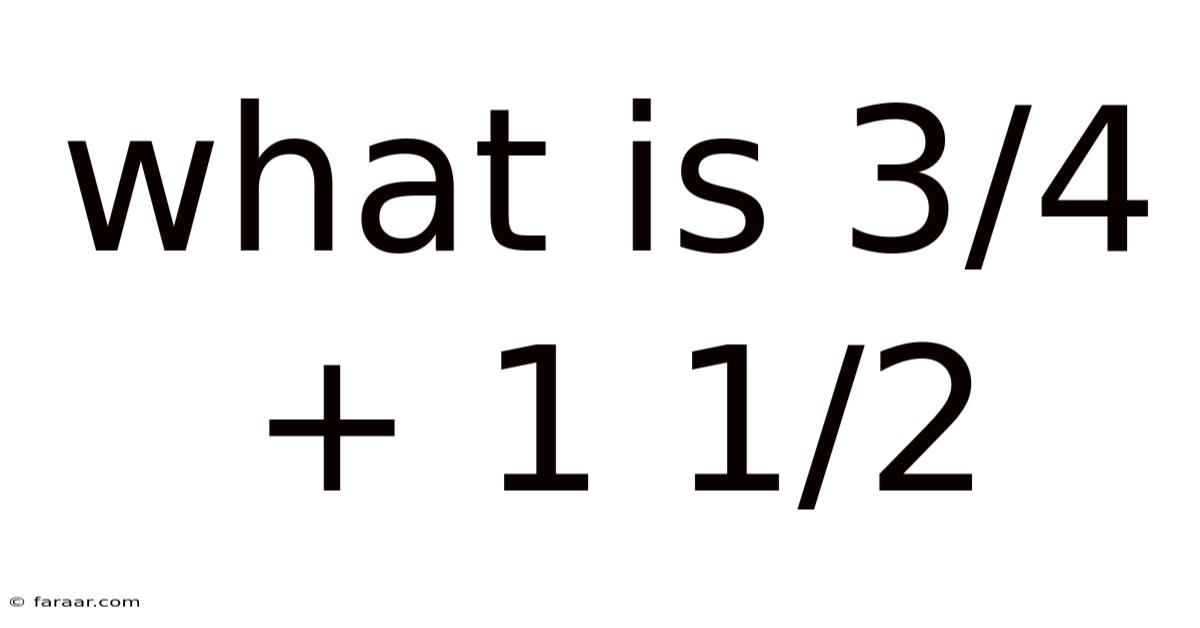
Table of Contents
Decoding Fractions: A Comprehensive Guide to Solving 3/4 + 1 1/2
Adding fractions might seem daunting at first, especially when dealing with mixed numbers like in the equation 3/4 + 1 1/2. This seemingly simple problem opens the door to understanding fundamental concepts in arithmetic, particularly fraction manipulation and equivalent fractions. This comprehensive guide will not only solve 3/4 + 1 1/2 but will also equip you with the skills and knowledge to tackle similar problems with confidence. We'll delve into the step-by-step process, explain the underlying mathematical principles, and address frequently asked questions to ensure a thorough understanding.
Understanding Fractions: A Quick Refresher
Before tackling the addition problem, let's refresh our understanding of fractions. A fraction represents a part of a whole. It's expressed as a ratio of two numbers: the numerator (the top number) and the denominator (the bottom number). The denominator indicates the number of equal parts the whole is divided into, while the numerator shows how many of those parts are being considered.
For example, in the fraction 3/4, the denominator (4) tells us the whole is divided into four equal parts, and the numerator (3) indicates we're considering three of those parts.
Mixed numbers, like 1 1/2, combine a whole number and a fraction. In this case, it represents one whole and one-half.
Step-by-Step Solution: 3/4 + 1 1/2
To add 3/4 and 1 1/2, we need to follow these steps:
Step 1: Convert Mixed Numbers to Improper Fractions
An improper fraction has a numerator larger than or equal to its denominator. It's easier to add fractions when they're all in this form. Let's convert 1 1/2 into an improper fraction:
- Multiply the whole number (1) by the denominator (2): 1 * 2 = 2
- Add the result to the numerator (1): 2 + 1 = 3
- Keep the same denominator (2): The improper fraction is 3/2
Now our equation becomes: 3/4 + 3/2
Step 2: Find a Common Denominator
Before adding fractions, they must have the same denominator. This is because we can only add parts of the same size. The least common denominator (LCD) for 4 and 2 is 4. We need to convert 3/2 to an equivalent fraction with a denominator of 4.
To do this, we multiply both the numerator and the denominator of 3/2 by 2:
(3 * 2) / (2 * 2) = 6/4
Now our equation is: 3/4 + 6/4
Step 3: Add the Numerators
Since the denominators are now the same, we can add the numerators directly:
3 + 6 = 9
Keep the same denominator (4): The result is 9/4
Step 4: Convert the Improper Fraction (if necessary) to a Mixed Number
The answer 9/4 is an improper fraction. To express it as a mixed number, we divide the numerator (9) by the denominator (4):
9 ÷ 4 = 2 with a remainder of 1
This means that 9/4 is equal to 2 wholes and 1/4. Therefore, the final answer is 2 1/4.
Mathematical Principles at Play
This seemingly simple addition problem highlights several crucial mathematical concepts:
-
Equivalent Fractions: Converting 3/2 to 6/4 demonstrates the concept of equivalent fractions. Multiplying or dividing both the numerator and denominator by the same non-zero number doesn't change the fraction's value. This is a fundamental principle in fraction manipulation.
-
Least Common Multiple (LCM): Finding the least common denominator (LCD) involves finding the LCM of the denominators. The LCM is the smallest number that is a multiple of both denominators. This ensures we're working with the same sized parts when adding the fractions.
-
Improper Fractions and Mixed Numbers: The conversion between improper fractions and mixed numbers shows the flexibility in representing fractional quantities. Improper fractions are often more convenient for calculations, while mixed numbers offer a more intuitive representation of the quantity.
Visualizing the Addition
Let's visualize the addition using diagrams:
Imagine a pizza cut into four slices (representing the denominator of 4). 3/4 represents three slices.
Now, imagine another pizza cut into two slices (representing the denominator of 2). 1 1/2 represents one whole pizza and one half of another. This is equivalent to 3 half-slices.
To combine these, we must express both in terms of quarters. One half-slice is equal to two quarter slices. Therefore, 1 1/2 is equal to 6 quarter slices.
Adding the three slices (3/4) and the six slices (6/4) gives us a total of nine quarter slices (9/4). This is equal to two whole pizzas and one quarter of a pizza (2 1/4).
Frequently Asked Questions (FAQ)
Q1: Can I add the fractions without finding a common denominator?
No, you cannot directly add the numerators of fractions with different denominators. The denominators represent the size of the parts, and you can only add parts of the same size.
Q2: What if the denominators have no common factors?
If the denominators are relatively prime (they share no common factors other than 1), then their least common multiple is simply their product. For example, if you were adding 1/3 and 1/5, the common denominator would be 15 (3 x 5).
Q3: Is there another way to solve this problem?
While the method described above is the most straightforward, you could also convert both fractions to decimals before adding them. 3/4 is 0.75, and 1 1/2 is 1.5. Adding these gives 2.25, which is equivalent to 2 1/4. However, the fraction method is generally preferred for maintaining accuracy and avoiding rounding errors.
Q4: How can I practice more fraction problems?
Practice is key to mastering fractions. Try working through various addition, subtraction, multiplication, and division problems with different types of fractions and mixed numbers. Online resources and textbooks offer a wealth of practice problems.
Conclusion: Mastering Fractions, One Step at a Time
Adding fractions, even those involving mixed numbers, is a fundamental skill in mathematics. By understanding the underlying principles and following the step-by-step process outlined above, you can confidently solve similar problems. Remember the importance of finding a common denominator, converting between improper fractions and mixed numbers, and visualizing the process. With consistent practice, you'll develop fluency and expertise in handling fractions and unlock a deeper understanding of mathematical concepts. The solution to 3/4 + 1 1/2, 2 1/4, is not just an answer, but a gateway to a broader understanding of numerical operations and problem-solving strategies. Embrace the challenge, and you'll find the world of fractions far less intimidating than it initially appeared.
Latest Posts
Latest Posts
-
Thank You Very Much In Arabic Language
Aug 27, 2025
-
30 Is What Percent Of 36
Aug 27, 2025
-
Find Three Consecutive Integers With A Sum Of 93
Aug 27, 2025
-
How To Find Area Of Parallelogram With Vectors
Aug 27, 2025
-
What Is 3 4 Cup Times 3
Aug 27, 2025
Related Post
Thank you for visiting our website which covers about What Is 3/4 + 1 1/2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.