What Is 3 4 Cup Times 3
faraar
Aug 27, 2025 · 6 min read
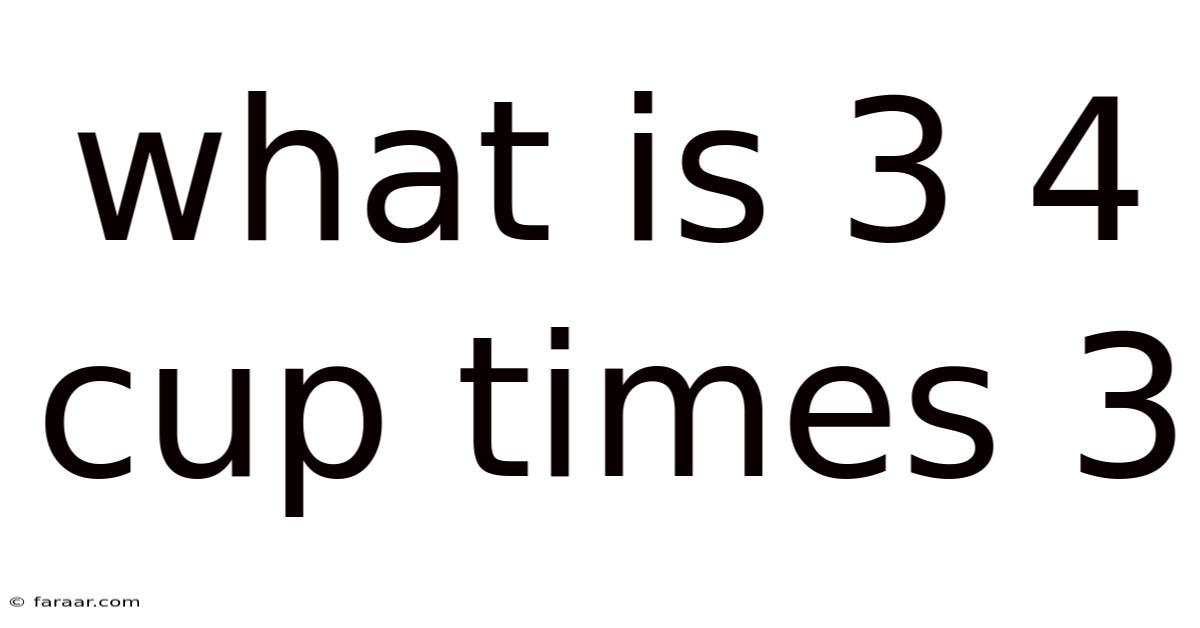
Table of Contents
What is 3/4 Cup Times 3? A Deep Dive into Fraction Multiplication
This article will explore the seemingly simple question: "What is 3/4 cup times 3?" While the answer might seem immediately obvious to some, this seemingly basic calculation provides a fantastic opportunity to delve into the fundamental principles of fraction multiplication, its practical applications in everyday life, particularly in cooking and baking, and even explore related mathematical concepts. We will also address common misconceptions and provide a step-by-step guide to solving similar problems. This guide will be particularly useful for students learning fractions and anyone needing a refresher on fraction arithmetic.
Understanding Fractions: A Quick Refresher
Before diving into the calculation, let's refresh our understanding of fractions. A fraction represents a part of a whole. It's written as a numerator (the top number) over a denominator (the bottom number), like this: a/b. The numerator indicates how many parts we have, and the denominator indicates how many equal parts the whole is divided into. In our problem, 3/4 represents three out of four equal parts of a cup.
Multiplying Fractions: The Basics
Multiplying fractions is surprisingly straightforward. To multiply two fractions, you simply multiply the numerators together and then multiply the denominators together. For example:
(a/b) * (c/d) = (a * c) / (b * d)
Solving 3/4 Cup Times 3
Now, let's apply this knowledge to our problem: 3/4 cup times 3. We can rewrite the whole number 3 as a fraction: 3/1. Now our problem becomes:
(3/4) * (3/1)
Following the rule for multiplying fractions:
- Multiply the numerators: 3 * 3 = 9
- Multiply the denominators: 4 * 1 = 4
Therefore, the answer is 9/4.
Converting Improper Fractions to Mixed Numbers
The result, 9/4, is an improper fraction because the numerator (9) is larger than the denominator (4). It's often more practical to express this as a mixed number, which combines a whole number and a fraction. To convert 9/4 to a mixed number:
- Divide the numerator by the denominator: 9 ÷ 4 = 2 with a remainder of 1.
- The quotient (2) becomes the whole number part of the mixed number.
- The remainder (1) becomes the numerator of the fraction, and the denominator remains the same (4).
Therefore, 9/4 is equivalent to 2 1/4 cups.
Practical Applications: Cooking and Baking
Understanding fraction multiplication is crucial in cooking and baking. Recipes often require precise measurements, and scaling recipes up or down necessitates accurate fraction calculations. Imagine you have a recipe that calls for 3/4 cup of flour, but you want to triple the recipe. Knowing that 3/4 cup times 3 equals 2 1/4 cups ensures you use the correct amount of flour, leading to better results. This applies to all ingredients, ensuring consistent and delicious outcomes.
Beyond the Basics: Extending the Concept
While the initial problem focused on a specific scenario, the underlying principles extend far beyond cooking. Fraction multiplication is fundamental to various fields:
- Construction and Engineering: Calculating material quantities, dimensions, and scaling blueprints.
- Finance: Determining portions of investments, calculating interest, and analyzing financial statements.
- Science: Measuring quantities, conducting experiments involving proportions, and analyzing data.
- Everyday Life: Sharing items, calculating discounts, understanding proportions in general.
Addressing Common Misconceptions
Several common mistakes can arise when working with fractions:
- Adding instead of multiplying: A common error is to add the numerator and denominator or add the whole number and the fraction. Remember, when multiplying fractions, you multiply the numerators and denominators separately.
- Incorrect conversion to mixed numbers: Mistakes can occur during the division process when converting an improper fraction to a mixed number. Carefully check your division and ensure the remainder is correctly incorporated into the fractional part.
- Not simplifying the fraction: After multiplying or converting, it's often beneficial to simplify the fraction to its lowest terms. For example, 6/8 can be simplified to 3/4 by dividing both the numerator and denominator by 2.
Step-by-Step Guide to Solving Similar Problems
Let's outline a step-by-step guide to tackle similar problems involving fraction multiplication:
- Identify the fractions: Write down the fractions involved in the problem. If a whole number is present, convert it into a fraction by placing it over 1 (e.g., 5 becomes 5/1).
- Multiply the numerators: Multiply the top numbers (numerators) of the fractions together.
- Multiply the denominators: Multiply the bottom numbers (denominators) together.
- Simplify the resulting fraction (if necessary): Reduce the fraction to its lowest terms by dividing both the numerator and denominator by their greatest common divisor (GCD).
- Convert to a mixed number (if necessary): If the resulting fraction is an improper fraction (numerator > denominator), convert it to a mixed number by dividing the numerator by the denominator. The quotient is the whole number part, and the remainder becomes the numerator of the fraction part. The denominator remains unchanged.
Frequently Asked Questions (FAQ)
Q: What if I need to multiply more than two fractions?
A: The process remains the same. Multiply all the numerators together and then multiply all the denominators together. Simplify the resulting fraction as needed.
Q: Can I multiply fractions and whole numbers directly without converting the whole number to a fraction?
A: While you can multiply a whole number directly to the numerator of a fraction, it is often simpler to convert the whole number into a fraction first for consistency and clarity in applying the multiplication rule.
Q: What if the fractions have different denominators?
A: In this case you first find a common denominator before you can add or subtract, but for multiplication you don't need a common denominator. Simply multiply the numerators and the denominators separately.
Q: How can I practice more fraction multiplication problems?
A: Numerous online resources, textbooks, and worksheets provide ample opportunities to practice fraction multiplication. Look for exercises that involve various combinations of proper and improper fractions, as well as whole numbers.
Conclusion
The question "What is 3/4 cup times 3?" serves as a springboard for understanding the fundamental principles of fraction multiplication. Beyond providing a simple answer (2 1/4 cups), it highlights the practical applications of this mathematical concept in various aspects of life, especially in cooking, baking, and numerous other fields. Mastering fraction multiplication is essential for anyone seeking to confidently tackle numerical problems involving parts of a whole. By understanding the underlying principles and practicing regularly, you can build a solid foundation in fractions and apply this knowledge to solve complex problems with ease. Remember to break down the problem into smaller, manageable steps, and always double-check your work for accuracy. With consistent effort, you’ll become proficient in this vital mathematical skill.
Latest Posts
Latest Posts
-
What Is 2 3 Of A Pound
Aug 27, 2025
-
Consider This Equilibrium Reaction At 400 K
Aug 27, 2025
-
How To Calculate The Average Volume
Aug 27, 2025
-
How Many Ounces In 1 Pound Of Cheese
Aug 27, 2025
-
What Is A Corresponding Ordered Pair
Aug 27, 2025
Related Post
Thank you for visiting our website which covers about What Is 3 4 Cup Times 3 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.