What Is 1/3 Of 2 1/2
faraar
Sep 13, 2025 · 5 min read
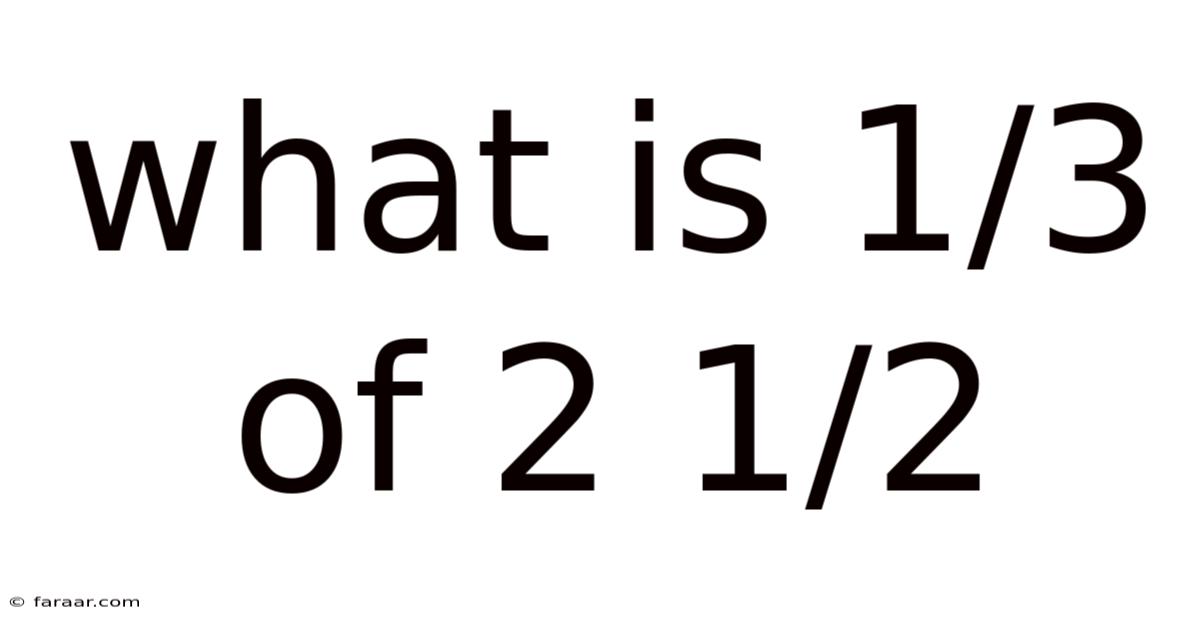
Table of Contents
What is 1/3 of 2 1/2? A Comprehensive Guide to Fraction Multiplication
This article will comprehensively explore the question, "What is 1/3 of 2 1/2?" We'll delve into the process of multiplying fractions, providing a step-by-step guide suitable for learners of all levels. We'll also explore the underlying mathematical concepts and address frequently asked questions. Understanding fraction multiplication is crucial for various mathematical applications, and this guide aims to build a solid foundation for confident problem-solving.
Understanding Fractions
Before diving into the calculation, let's refresh our understanding of fractions. A fraction represents a part of a whole. It consists of two numbers: the numerator (the top number) and the denominator (the bottom number). The numerator indicates how many parts we have, while the denominator indicates how many equal parts the whole is divided into. For example, in the fraction 1/3, the numerator is 1 and the denominator is 3. This means we have 1 out of 3 equal parts.
Mixed numbers, like 2 1/2, combine a whole number and a fraction. 2 1/2 means we have two whole units and an additional half unit.
Converting Mixed Numbers to Improper Fractions
To multiply fractions efficiently, it's often easier to work with improper fractions. An improper fraction has a numerator greater than or equal to its denominator. To convert a mixed number to an improper fraction, we follow these steps:
- Multiply the whole number by the denominator: In 2 1/2, we multiply 2 (whole number) by 2 (denominator) = 4.
- Add the numerator: Add the result from step 1 to the numerator: 4 + 1 = 5.
- Keep the same denominator: The denominator remains the same, which is 2.
Therefore, 2 1/2 is equivalent to the improper fraction 5/2.
Multiplying Fractions: A Step-by-Step Guide
Now, let's tackle the multiplication: 1/3 of 2 1/2. Remember, "of" in this context means multiplication. So, we need to calculate (1/3) x (2 1/2).
-
Convert to improper fractions: As discussed earlier, we'll convert 2 1/2 to 5/2. Our problem now becomes (1/3) x (5/2).
-
Multiply the numerators: Multiply the numerators together: 1 x 5 = 5.
-
Multiply the denominators: Multiply the denominators together: 3 x 2 = 6.
-
Form the resulting fraction: The result of the multiplication is 5/6.
Therefore, 1/3 of 2 1/2 is 5/6.
Simplifying Fractions
Sometimes, the resulting fraction can be simplified. A fraction is simplified when the numerator and denominator have no common factors other than 1. In our case, 5/6 is already in its simplest form because 5 and 6 share no common factors greater than 1.
Visualizing the Calculation
Let's visualize this using a diagram. Imagine a rectangle representing 2 1/2 units. Divide this rectangle into 6 equal parts (the denominator of our final answer). 1/3 of this rectangle would be 2/6 of the total rectangle (two out of six parts). Since the rectangle represents 5/2 units, 1/3 of that rectangle represents (1/3)*(5/2) = 5/6.
Real-World Applications
Understanding fraction multiplication has practical applications in various everyday situations. Imagine you have 2 1/2 pizzas, and you want to give 1/3 of them to your friends. Using the calculation above, you'd be giving away 5/6 of a pizza.
This knowledge is also crucial in:
- Cooking and baking: Adjusting recipes, scaling ingredients up or down.
- Construction and engineering: Calculating material requirements.
- Finance: Calculating percentages, portions of payments, or discounts.
Different Approaches to Fraction Multiplication
While the method described above is the most common and straightforward approach, let's explore an alternative method that might be helpful for some:
-
Multiply the whole number first: We can initially multiply 1/3 by the whole number 2, resulting in 2/3.
-
Multiply the fraction part: Now multiply 1/3 by 1/2, which gives 1/6.
-
Add the results: Add the results from steps 1 and 2: 2/3 + 1/6. To add these fractions, we need a common denominator, which is 6. So, we rewrite 2/3 as 4/6. Adding 4/6 and 1/6 gives us 5/6.
This alternative approach leads to the same answer, highlighting the flexibility in approaching fraction multiplication problems.
Frequently Asked Questions (FAQ)
Q: Can I use a calculator to solve this problem?
A: Yes, many calculators, including scientific calculators and online calculators, can handle fraction multiplication. However, understanding the underlying mathematical principles is vital for solving more complex problems and building mathematical intuition.
Q: What if I have more complex fractions to multiply?
A: The same principles apply. Convert all mixed numbers to improper fractions, multiply the numerators, multiply the denominators, and simplify the resulting fraction if possible.
Q: Why is it important to simplify fractions?
A: Simplifying fractions makes the result easier to understand and work with. It also ensures you're presenting your answer in its most concise and efficient form.
Q: Are there any shortcuts for multiplying fractions?
A: You can sometimes simplify before multiplying. If a numerator and a denominator share a common factor, you can cancel them out before performing the multiplication. This can make the calculations easier.
Conclusion
This article comprehensively explored the calculation of 1/3 of 2 1/2. We've not only solved the problem but also delved into the fundamental concepts of fraction multiplication, converting mixed numbers to improper fractions, and simplifying fractions. Through various methods and real-world examples, we've highlighted the importance and practical applications of this crucial mathematical skill. Remember, the key is to break down the problem into manageable steps, understand the underlying principles, and practice regularly to build confidence and mastery. Mastering fraction multiplication opens doors to more advanced mathematical concepts and problem-solving abilities. Continue exploring, practicing, and deepening your mathematical understanding!
Latest Posts
Latest Posts
-
2 3 Cup X 2 Equals
Sep 13, 2025
-
How Many Moles Are In 25 0 Grams Of Water
Sep 13, 2025
-
What Is The Approximate Area Of The Hexagon
Sep 13, 2025
-
The Product Of Two And A Number Plus One
Sep 13, 2025
-
How Much Are Bowling Shoe Rentals
Sep 13, 2025
Related Post
Thank you for visiting our website which covers about What Is 1/3 Of 2 1/2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.