What Is 1 1/3 + 1 1/3
faraar
Aug 26, 2025 · 5 min read
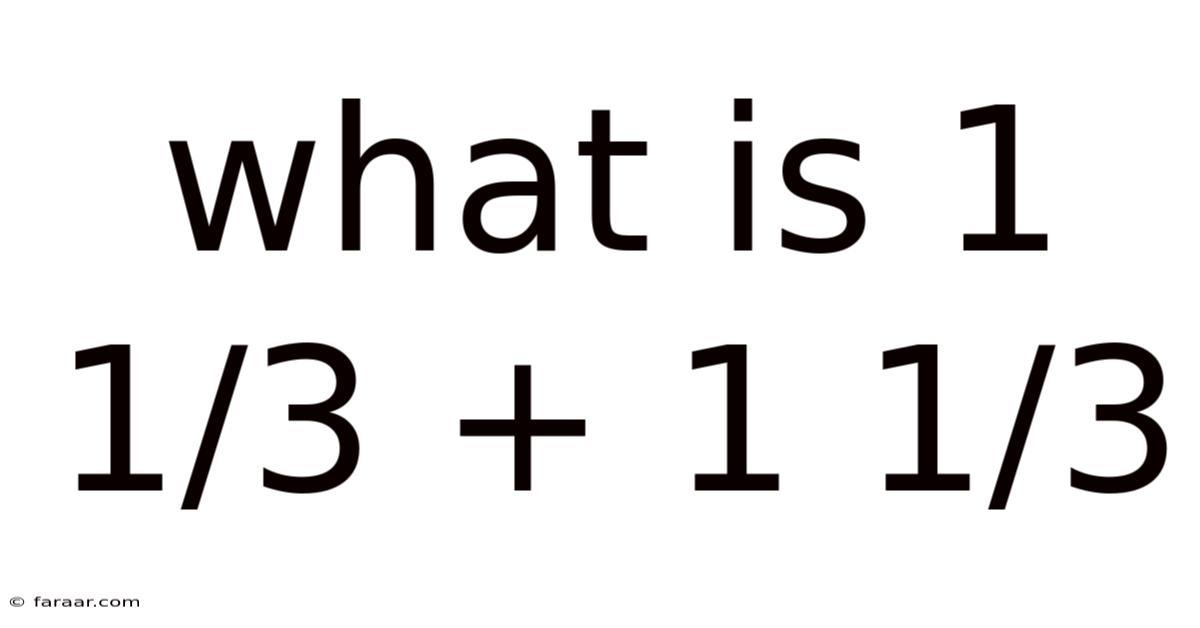
Table of Contents
Decoding 1 1/3 + 1 1/3: A Deep Dive into Fraction Addition
Adding fractions might seem like a simple task, especially when dealing with seemingly straightforward numbers like 1 1/3. However, a thorough understanding of this seemingly basic operation lays the groundwork for more complex mathematical concepts. This article will not just solve 1 1/3 + 1 1/3, but will also explore the underlying principles of fraction addition, delve into different methods of solving the problem, and even touch upon the practical applications of this knowledge. We'll also address common misconceptions and frequently asked questions, ensuring a comprehensive understanding of this fundamental arithmetic skill.
Introduction: Understanding Fractions and Mixed Numbers
Before we tackle the problem of 1 1/3 + 1 1/3, let's refresh our understanding of fractions and mixed numbers. A fraction represents a part of a whole. It consists of a numerator (the top number) and a denominator (the bottom number). The denominator indicates how many equal parts the whole is divided into, while the numerator shows how many of those parts are being considered.
A mixed number, like 1 1/3, combines a whole number and a fraction. In this case, 1 1/3 represents one whole unit plus one-third of another unit. Understanding the composition of mixed numbers is crucial for efficient addition.
Method 1: Converting to Improper Fractions
The most common and generally preferred method for adding mixed numbers involves converting them into improper fractions. An improper fraction has a numerator that is greater than or equal to its denominator. To convert 1 1/3 to an improper fraction, we multiply the whole number (1) by the denominator (3), add the numerator (1), and keep the same denominator:
(1 x 3) + 1 = 4
Therefore, 1 1/3 is equal to 4/3.
Now, we can easily add the two improper fractions:
4/3 + 4/3 = 8/3
This improper fraction can then be converted back into a mixed number. We divide the numerator (8) by the denominator (3):
8 ÷ 3 = 2 with a remainder of 2
Therefore, 8/3 is equivalent to 2 2/3.
Thus, 1 1/3 + 1 1/3 = 2 2/3
Method 2: Adding Whole Numbers and Fractions Separately
Another approach involves adding the whole numbers and the fractional parts separately. This method is particularly intuitive and easier to visualize:
- Add the whole numbers: 1 + 1 = 2
- Add the fractions: 1/3 + 1/3 = 2/3
Combine the results: 2 + 2/3 = 2 2/3
Again, we arrive at the solution: 1 1/3 + 1 1/3 = 2 2/3
Method 3: Visual Representation using Diagrams
Visual aids can greatly enhance understanding, particularly for those who find abstract mathematical concepts challenging. We can represent 1 1/3 using diagrams:
Imagine a circle divided into three equal parts. 1 1/3 would be represented by one whole circle and one shaded segment of a second circle divided into three equal parts. Adding another 1 1/3 would involve adding another whole circle and another shaded segment. The result would visually represent two whole circles and two shaded segments, confirming our answer of 2 2/3.
The Importance of Understanding Common Denominators
When adding fractions with different denominators, finding a common denominator is crucial. The common denominator is a multiple of both denominators. Let's consider an example where we add 1 1/3 and 1 1/2.
First, convert to improper fractions: 4/3 and 3/2. The least common multiple of 3 and 2 is 6, so we find equivalent fractions with a denominator of 6:
4/3 = (4 x 2) / (3 x 2) = 8/6 3/2 = (3 x 3) / (2 x 3) = 9/6
Now, we can add: 8/6 + 9/6 = 17/6
Converting back to a mixed number: 17 ÷ 6 = 2 with a remainder of 5. Therefore, 17/6 = 2 5/6. This demonstrates the importance of common denominators for accurate fraction addition. In our original problem, however, the denominators were already the same, simplifying the process.
Real-World Applications of Fraction Addition
Understanding fraction addition isn't just an academic exercise. It has numerous practical applications in daily life, including:
- Cooking and Baking: Many recipes require precise measurements, often involving fractions of cups or teaspoons.
- Sewing and Crafting: Accurate measurements are essential in these fields, often involving fractions of inches or centimeters.
- Construction and Engineering: Precision is crucial, necessitating the use of fractions and their addition in calculations.
- Finance: Calculating portions of budgets, interest rates, or investment returns often involves fractions.
- Data Analysis: Representing and interpreting data often involves fractions and their manipulation.
Frequently Asked Questions (FAQ)
Q1: Can I add mixed numbers without converting them to improper fractions?
A1: Yes, as shown in Method 2, you can add the whole number parts and fractional parts separately, then combine the results. However, many find the improper fraction method more systematic and less prone to errors.
Q2: What if the fractions have different denominators?
A2: You need to find a common denominator before adding the fractions. This involves finding the least common multiple (LCM) of the denominators.
Q3: Are there any shortcuts for adding fractions?
A3: For simple fractions with the same denominator, as in our example, the addition is straightforward. For more complex fractions, understanding equivalent fractions and LCMs is key to efficient calculation.
Q4: Why is understanding fractions important?
A4: Fractions are fundamental to understanding many aspects of mathematics and science. They form the basis for decimals, percentages, ratios, and proportions. A solid grasp of fractions is essential for success in various academic and professional fields.
Conclusion: Mastering the Fundamentals
Adding fractions, even seemingly simple examples like 1 1/3 + 1 1/3, is a crucial building block in mathematics. This article has explored different methods for solving this problem, highlighting the importance of understanding fractions, mixed numbers, improper fractions, and common denominators. By mastering these fundamentals, you not only solve this specific problem but also gain a solid foundation for tackling more complex mathematical challenges. The seemingly simple act of adding 1 1/3 and 1 1/3 unveils a world of mathematical concepts and practical applications, emphasizing the significance of mastering even the most basic arithmetic principles. Remember, a strong foundation in mathematics opens doors to countless opportunities in various fields of study and professional endeavors.
Latest Posts
Latest Posts
-
How To Spell Do In Spanish
Aug 27, 2025
-
Why Do The Montagues And The Capulets Hate Each Other
Aug 27, 2025
-
2 More Than 3 Times A Number X Is 17
Aug 27, 2025
-
What Is The Square Root Pi
Aug 27, 2025
-
Curly Hair Gene Dominant Or Recessive
Aug 27, 2025
Related Post
Thank you for visiting our website which covers about What Is 1 1/3 + 1 1/3 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.