2 More Than 3 Times A Number X Is 17
faraar
Aug 27, 2025 · 6 min read
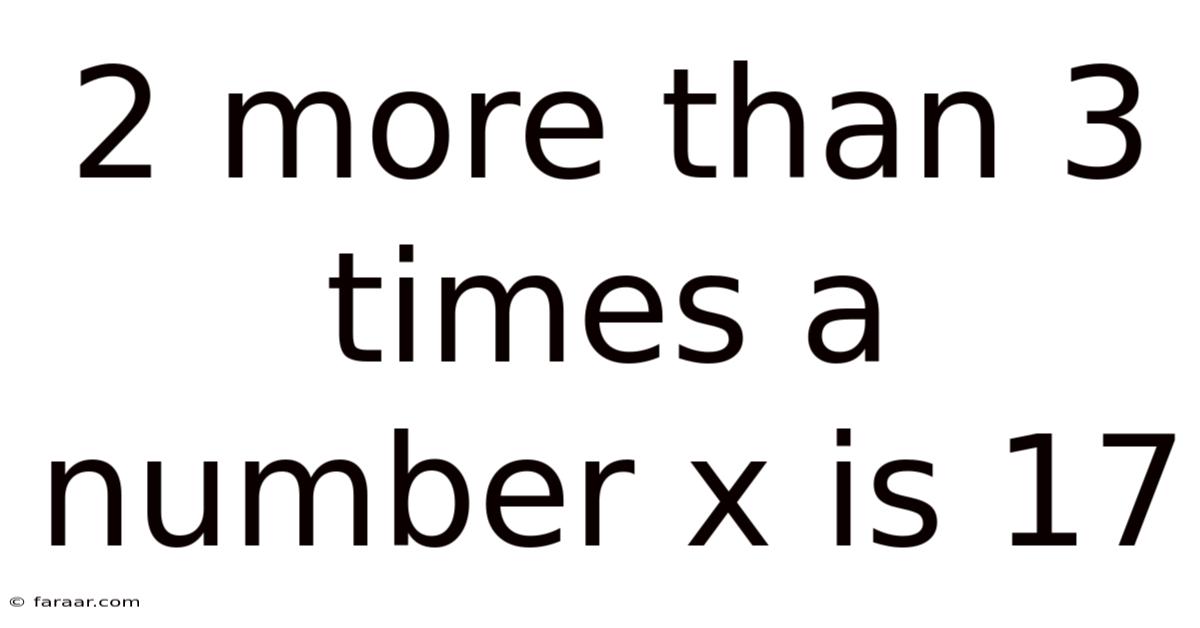
Table of Contents
2 More Than 3 Times a Number x is 17: Unraveling the Mathematical Mystery
This article explores the seemingly simple mathematical statement: "2 more than 3 times a number x is 17." We'll delve into how to solve this equation, understand the underlying principles, and even explore the broader context of similar problems. This seemingly basic problem provides a fantastic gateway to understanding algebraic concepts and problem-solving strategies. Whether you're a student struggling with algebra or simply curious about the logic behind mathematical equations, this guide will illuminate the path to the solution and beyond.
Understanding the Problem: Translating Words into Math
Before diving into the solution, let's break down the sentence into its core mathematical components. The phrase "a number x" simply represents an unknown value, which we denote as 'x'. "3 times a number x" translates directly into the algebraic expression 3x. The phrase "2 more than" indicates addition, signifying that we add 2 to the result of 3x. Finally, "is 17" signifies equality, meaning the entire expression equals 17.
Therefore, the complete mathematical equation derived from the sentence is:
3x + 2 = 17
This equation forms the basis of our problem-solving process. We will use the principles of algebra to isolate 'x' and find its value.
Solving the Equation: Step-by-Step Guide
Solving the equation requires a systematic approach, utilizing the fundamental principles of algebra. The goal is to isolate the variable 'x' on one side of the equation, revealing its value. Let's proceed step-by-step:
Step 1: Subtract 2 from both sides:
To begin isolating 'x', we need to remove the constant term (+2) from the left-hand side of the equation. We achieve this by subtracting 2 from both sides of the equation, maintaining the balance of the equation:
3x + 2 - 2 = 17 - 2
This simplifies to:
3x = 15
Step 2: Divide both sides by 3:
Now, we have 3 multiplied by 'x'. To isolate 'x', we perform the inverse operation – division. We divide both sides of the equation by 3:
3x / 3 = 15 / 3
This results in:
x = 5
Therefore, the solution to the equation is x = 5. This means that the unknown number is 5.
Verification: Checking Our Answer
It's crucial to verify our solution. We substitute the value of x (5) back into the original equation to ensure it holds true:
3x + 2 = 17
3(5) + 2 = 17
15 + 2 = 17
17 = 17
The equation holds true, confirming that our solution, x = 5, is correct.
The Broader Context: Understanding Linear Equations
The problem "2 more than 3 times a number x is 17" is a classic example of a linear equation. Linear equations are algebraic equations where the highest power of the variable is 1. They are characterized by a straight-line graph when plotted on a Cartesian coordinate system. Understanding linear equations is fundamental to many areas of mathematics, science, and engineering.
Applications of Linear Equations in Real-World Scenarios
Linear equations aren't just abstract mathematical concepts; they have numerous real-world applications. Here are a few examples:
-
Calculating Costs: Imagine you're renting a car. The rental cost might be a fixed daily fee plus a charge per mile driven. This scenario can be modeled using a linear equation, where the total cost is a function of the number of miles driven.
-
Determining Speed and Distance: The relationship between speed, distance, and time is often represented by a linear equation. If you know the speed and time, you can calculate the distance traveled.
-
Analyzing Financial Growth: Simple interest calculations involve linear equations. The total amount in a savings account after a certain period is linearly related to the initial amount, interest rate, and time.
-
Predicting Trends: In data analysis, linear regression is used to find the best-fitting line through a set of data points. This line can be used to predict future values based on the observed trend.
Different Approaches to Solving the Equation
While the step-by-step method presented earlier is straightforward, there are other approaches to solving the equation 3x + 2 = 17. These alternative methods can enhance your understanding and provide flexibility in tackling similar problems.
1. Using Inverse Operations: This approach directly utilizes inverse operations to isolate the variable. We start by subtracting 2 from both sides, then dividing by 3, as demonstrated in the step-by-step method.
2. Graphical Method: This method involves plotting the equation 3x + 2 = 17 on a graph. The x-coordinate of the point where the line intersects the x-axis (y = 0) represents the solution.
3. Trial and Error: While less systematic, this approach involves substituting different values of x into the equation until you find one that satisfies the equality. This method is less efficient for complex equations but can be useful for simpler ones.
Extending the Concept: More Complex Problems
The fundamental principles used to solve "2 more than 3 times a number x is 17" can be extended to solve more complex linear equations. These might involve multiple variables, fractions, or decimals. However, the core strategy remains the same: manipulate the equation using algebraic operations to isolate the variable of interest.
Frequently Asked Questions (FAQ)
Q: What if the problem involved subtraction instead of addition?
A: If the problem were "2 less than 3 times a number x is 17," the equation would be 3x - 2 = 17. The solution process would be similar, but instead of subtracting 2, you would add 2 to both sides in the first step.
Q: Can this type of problem involve negative numbers?
A: Absolutely! The variable 'x' could potentially have a negative value. The solution process remains the same, even if the result is a negative number.
Q: What if the equation is more complex, with multiple variables?
A: Solving equations with multiple variables usually requires the use of systems of equations, often involving techniques like substitution or elimination.
Conclusion: Mastering the Fundamentals
The seemingly simple problem, "2 more than 3 times a number x is 17," serves as a powerful introduction to the world of algebra and equation solving. By understanding the steps involved in solving this equation, you've grasped a fundamental skill applicable to a wide range of mathematical problems and real-world applications. Remember the core principles: translate the problem into a mathematical equation, utilize algebraic manipulation to isolate the variable, and always verify your solution. With practice and a solid understanding of these concepts, you'll confidently navigate more complex mathematical challenges. The journey of mastering algebra begins with these foundational steps, paving the way for a deeper appreciation of mathematical concepts and their practical applications.
Latest Posts
Latest Posts
-
How To Know If A Function Is Invertible
Aug 27, 2025
-
What Is The Approximate Area Of The Circle Shown Below
Aug 27, 2025
-
Enthalpy Of Solution For Ammonium Nitrate
Aug 27, 2025
-
What Is 3 4 1 1 2
Aug 27, 2025
-
How To Solve The Polynomial Equation
Aug 27, 2025
Related Post
Thank you for visiting our website which covers about 2 More Than 3 Times A Number X Is 17 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.