V Πr 2h Solve For H
faraar
Sep 14, 2025 · 5 min read
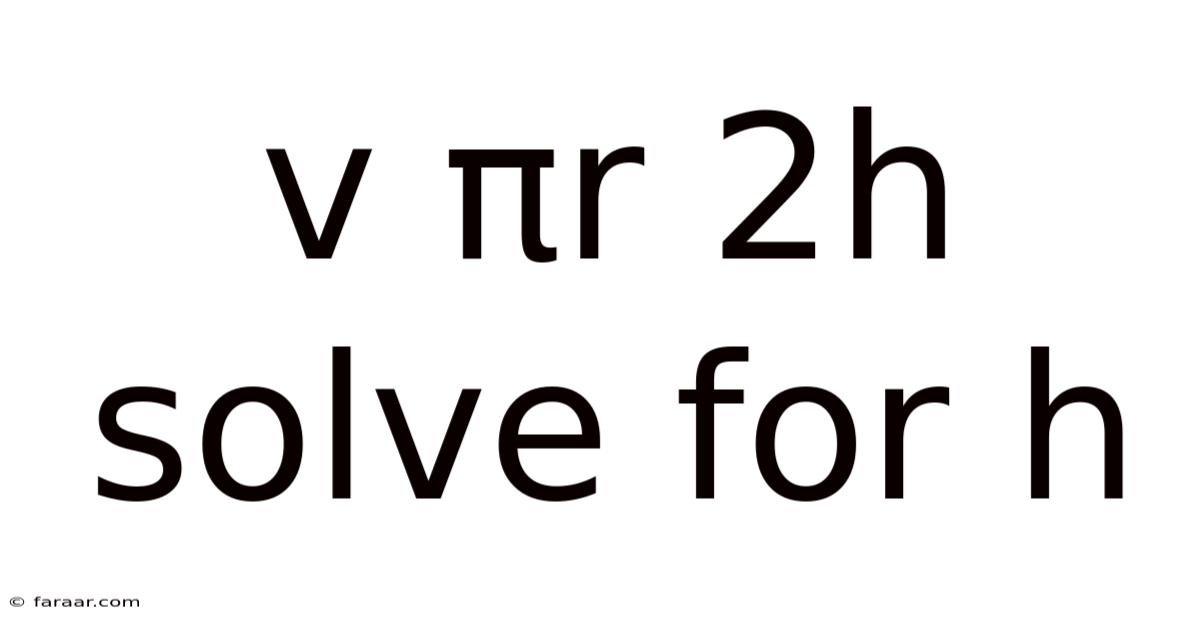
Table of Contents
Solving for h: Unraveling the Volume of a Cylinder
Understanding the formula for the volume of a cylinder, V = πr²h, is a fundamental concept in geometry. This formula allows us to calculate the volume of cylindrical objects – from simple cans of soup to complex industrial tanks. But what happens when you know the volume and the radius, and you need to find the height (h)? This article will guide you through the process of solving for 'h' in the equation V = πr²h, explaining the steps involved and providing practical examples to solidify your understanding. We'll also explore the underlying mathematical principles and address frequently asked questions.
Understanding the Formula: V = πr²h
Before we delve into solving for 'h', let's briefly review the components of the formula V = πr²h:
-
V: Represents the volume of the cylinder. Volume is the amount of three-dimensional space occupied by an object. It's typically measured in cubic units (e.g., cubic centimeters, cubic meters, cubic inches).
-
π (Pi): A mathematical constant, approximately equal to 3.14159. It represents the ratio of a circle's circumference to its diameter.
-
r: Represents the radius of the cylinder's base. The radius is the distance from the center of the circular base to any point on the circumference.
-
h: Represents the height of the cylinder. The height is the perpendicular distance between the two circular bases.
Solving for h: A Step-by-Step Guide
To solve for 'h', we need to isolate 'h' on one side of the equation. We can achieve this using algebraic manipulation. Here's a step-by-step guide:
1. Start with the original formula:
V = πr²h
2. Divide both sides by πr²: To isolate 'h', we need to get rid of everything else on that side of the equation. Since 'πr²' is multiplied by 'h', we perform the inverse operation – division.
V / (πr²) = (πr²h) / (πr²)
3. Simplify the equation:
The πr² on the right side cancels out, leaving us with:
h = V / (πr²)
This is the formula to calculate the height (h) of a cylinder when you know its volume (V) and radius (r).
Practical Examples: Putting the Formula into Action
Let's work through a few examples to solidify your understanding:
Example 1:
A cylindrical water tank has a volume of 150 cubic meters and a radius of 3 meters. What is its height?
- Given: V = 150 m³, r = 3 m
- Formula: h = V / (πr²)
- Calculation: h = 150 m³ / (π * (3 m)²) ≈ 150 m³ / (3.14159 * 9 m²) ≈ 150 m³ / 28.27431 m² ≈ 5.305 m
Therefore, the height of the water tank is approximately 5.31 meters.
Example 2:
A cylindrical can of soup has a volume of 500 cubic centimeters and a height of 10 centimeters. What is its radius?
This example requires a slight modification. While the question asks for the radius, we can use the height formula derived above to solve for the radius.
- Given: V = 500 cm³, h = 10 cm
- Formula: r² = V / (πh) (Rearranging the formula to solve for r²)
- Calculation: r² = 500 cm³ / (π * 10 cm) ≈ 500 cm³ / 31.4159 cm ≈ 15.915 cm²
- Find the square root: r = √15.915 cm² ≈ 3.99 cm
Therefore, the radius of the soup can is approximately 4 centimeters.
Mathematical Justification: Why Does This Work?
The process of solving for 'h' relies on fundamental algebraic principles. The core idea is to perform inverse operations to isolate the variable of interest. Since 'h' is multiplied by πr², we divide both sides of the equation by πr² to maintain the equality while isolating 'h'. This is based on the property of equality which states that if you perform the same operation on both sides of an equation, the equality remains true. This ensures we haven't changed the inherent relationship between the volume, radius, and height of the cylinder.
Beyond the Basics: Applications and Extensions
The formula V = πr²h, and its manipulation to solve for different variables, has widespread applications beyond simple geometry problems. It's crucial in:
-
Engineering: Calculating the volume of pipes, tanks, and other cylindrical structures is vital for design and construction.
-
Manufacturing: Determining the amount of material needed to produce cylindrical products.
-
Physics: Calculating the volume of cylindrical containers in fluid mechanics and thermodynamics.
-
Data Analysis: Cylindrical coordinates are used in various data analysis and visualization techniques.
Frequently Asked Questions (FAQ)
Q: What if I don't have a calculator with π?
A: You can use the approximation π ≈ 3.14 or π ≈ 22/7 for simpler calculations. Keep in mind that this will slightly reduce the accuracy of your result.
Q: Can I use this formula for cylinders with different bases?
A: No. This formula specifically applies to right circular cylinders, meaning cylinders with circular bases and perpendicular height. Other cylindrical shapes will require different formulas.
Q: What if the cylinder is slanted?
A: The formula V = πr²h is only valid for right cylinders. For slanted cylinders (oblique cylinders), the calculation is more complex and involves considering the slant height and the area of the parallelogram-shaped side. The formula becomes considerably more intricate.
Q: Are there units I should always use?
A: Consistency in units is critical. If the radius is in centimeters, the volume should be in cubic centimeters, and the height will also be in centimeters. Using mixed units will lead to inaccurate results.
Conclusion: Mastering the Cylinder's Height
Solving for 'h' in the equation V = πr²h is a straightforward yet essential skill in mathematics and various scientific fields. By understanding the underlying principles of algebraic manipulation and applying the derived formula (h = V / (πr²)), you can confidently calculate the height of a cylinder given its volume and radius. Remember to always check your units for consistency, and don't hesitate to use approximations of π if a calculator isn't readily available. With practice, this process will become second nature, empowering you to tackle more complex geometric problems with ease. The ability to manipulate this seemingly simple formula provides a strong foundation for further exploration of more advanced geometric concepts and their real-world applications.
Latest Posts
Latest Posts
-
How Many Molecules In 2 0 Moles
Sep 14, 2025
-
Fourteen Decreased By Three Times Four
Sep 14, 2025
-
Sign Language Classes Las Vegas Nv
Sep 14, 2025
-
Which Type Of Reproduction Produces Offspring With More Genetic Variation
Sep 14, 2025
-
Are Vertical Angles Supplementary Or Congruent
Sep 14, 2025
Related Post
Thank you for visiting our website which covers about V Πr 2h Solve For H . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.