Fourteen Decreased By Three Times Four
faraar
Sep 14, 2025 · 5 min read
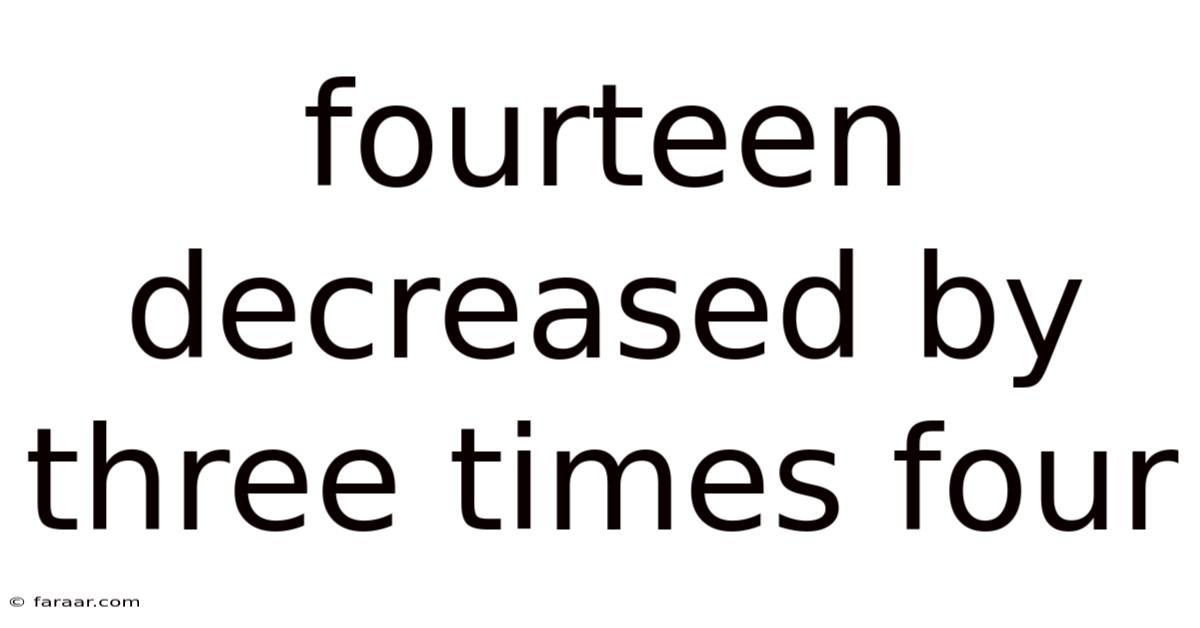
Table of Contents
Fourteen Decreased by Three Times Four: A Deep Dive into Mathematical Operations
This article explores the seemingly simple mathematical phrase "fourteen decreased by three times four," breaking it down step-by-step to understand not only the solution but also the underlying mathematical principles and the broader context of order of operations. We'll delve into the concept of decreasing, multiplication, and the importance of following a specific sequence to arrive at the correct answer. This detailed explanation is perfect for anyone looking to improve their understanding of basic arithmetic, particularly for students learning order of operations (PEMDAS/BODMAS).
Understanding the Problem: Deconstructing the Phrase
The phrase "fourteen decreased by three times four" might seem straightforward, but understanding its components is crucial. Let's break it down:
-
Fourteen: This is our starting number, the base value we'll be working with.
-
Decreased by: This indicates subtraction. We're taking something away from fourteen.
-
Three times four: This signifies multiplication. We need to calculate the product of three and four before proceeding with the subtraction.
The problem essentially asks us to perform a subtraction operation where the number being subtracted is the result of a multiplication operation. This highlights the importance of the order of operations.
The Order of Operations: PEMDAS/BODMAS
Before we solve the problem, it's essential to understand the order of operations, often remembered by the acronyms PEMDAS (Parentheses, Exponents, Multiplication and Division, Addition and Subtraction) or BODMAS (Brackets, Orders, Division and Multiplication, Addition and Subtraction). Both acronyms represent the same order:
-
Parentheses/Brackets: Calculations within parentheses or brackets are performed first.
-
Exponents/Orders: Exponents (powers) and roots are calculated next.
-
Multiplication and Division: These operations are performed from left to right.
-
Addition and Subtraction: These operations are performed from left to right.
Following this order ensures that we arrive at the correct answer, regardless of the complexity of the expression.
Solving "Fourteen Decreased by Three Times Four"
Now, let's apply the order of operations to solve our problem:
-
Multiplication: First, we calculate "three times four," which is 3 x 4 = 12.
-
Subtraction: Next, we perform the subtraction: "fourteen decreased by twelve" is 14 - 12 = 2.
Therefore, the solution to "fourteen decreased by three times four" is 2.
Visual Representation: Making it Clearer
Sometimes, a visual representation can aid understanding. We can represent the problem using a simple diagram:
14 - (3 x 4) = ?
14 - 12 = 2
This clearly shows the two steps involved: first the multiplication, then the subtraction. This method is particularly useful for visualizing more complex mathematical expressions.
Extending the Concept: Similar Problems and Variations
Understanding this basic problem allows us to tackle more complex variations. Consider these examples:
-
Twenty decreased by five times three: Following the same order of operations, we first calculate 5 x 3 = 15, then 20 - 15 = 5. The answer is 5.
-
Thirty-six increased by two times eight: Notice that "increased by" indicates addition. First, calculate 2 x 8 = 16, then 36 + 16 = 52. The answer is 52.
-
(Twelve minus four) multiplied by five: Here, parentheses take precedence. We calculate 12 - 4 = 8 first, and then 8 x 5 = 40. The answer is 40. This example emphasizes the significance of parentheses in altering the order of operations.
These examples highlight the adaptability of the order of operations principle across a range of mathematical expressions. The key is always to follow the PEMDAS/BODMAS rules consistently.
The Importance of Precision in Mathematical Language
The precise wording of the problem is crucial. Consider the subtle difference between "fourteen decreased by three times four" and "fourteen decreased by three, times four." The first phrase, as we've discussed, results in 2. The second phrase, however, is ambiguous and requires careful interpretation. It could be interpreted as (14 - 3) x 4 = 44, or possibly (14-3) x 4 = 11 x 4 = 44. This emphasizes that mathematical language must be unambiguous to ensure correct calculation.
Real-World Applications: Where This Matters
While this might seem like a simple arithmetic problem, the principles involved have wide-ranging applications in various fields:
-
Computer Programming: Order of operations is fundamental in programming, dictating the sequence of calculations within code.
-
Engineering and Physics: Accurate calculations are crucial in engineering and physics, where even small errors can have significant consequences.
-
Financial Calculations: From calculating interest to budgeting, accurate mathematical operations are essential in finance.
-
Data Analysis: Understanding order of operations is critical for correctly interpreting and manipulating data.
In essence, mastering the order of operations is not just about solving simple arithmetic problems; it's a foundational skill crucial for success in numerous academic and professional disciplines.
Frequently Asked Questions (FAQ)
Q1: What happens if there are multiple multiplication and division operations in the same expression?
A1: In such cases, perform these operations from left to right, adhering to the order of operations.
Q2: Can I use a calculator to solve this type of problem?
A2: Yes, most calculators will automatically follow the order of operations (PEMDAS/BODMAS). However, understanding the principles is still essential to interpret results and avoid errors.
Q3: Why is the order of operations important?
A3: The order of operations ensures consistency and prevents ambiguity in mathematical expressions. Without it, different people might arrive at different answers for the same problem.
Q4: Are there any exceptions to the order of operations?
A4: While the general principles of PEMDAS/BODMAS are widely accepted, specific contexts or specialized mathematical notations might have their own conventions. However, these are usually clearly defined and explained within the relevant context.
Q5: How can I improve my understanding of the order of operations?
A5: Practice is key! Solve numerous problems of varying complexity, focusing on understanding each step. Online resources and textbooks provide ample practice opportunities.
Conclusion: Mastering the Fundamentals
This detailed exploration of "fourteen decreased by three times four" has revealed more than just a simple arithmetic solution. It's highlighted the importance of understanding the order of operations (PEMDAS/BODMAS), the precision required in mathematical language, and the broad applicability of these principles across various disciplines. By mastering these fundamental concepts, you build a strong foundation for more complex mathematical challenges and enhance your problem-solving skills in diverse fields. Remember that consistent practice and a focus on understanding the underlying principles are crucial for achieving mastery. Keep practicing, and you'll become increasingly confident in tackling any mathematical expression you encounter.
Latest Posts
Latest Posts
-
Is Ionization Energy Positive Or Negative
Sep 14, 2025
-
Select All Of The Following That Are Like Radicals
Sep 14, 2025
-
Does F2 Have Dipole Dipole Forces
Sep 14, 2025
-
Why Is Water Liquid At Room Temperature
Sep 14, 2025
-
What Is The Molecular Geometry Of Ozone O3
Sep 14, 2025
Related Post
Thank you for visiting our website which covers about Fourteen Decreased By Three Times Four . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.