The Sum Of Six And A Number
faraar
Sep 18, 2025 · 6 min read
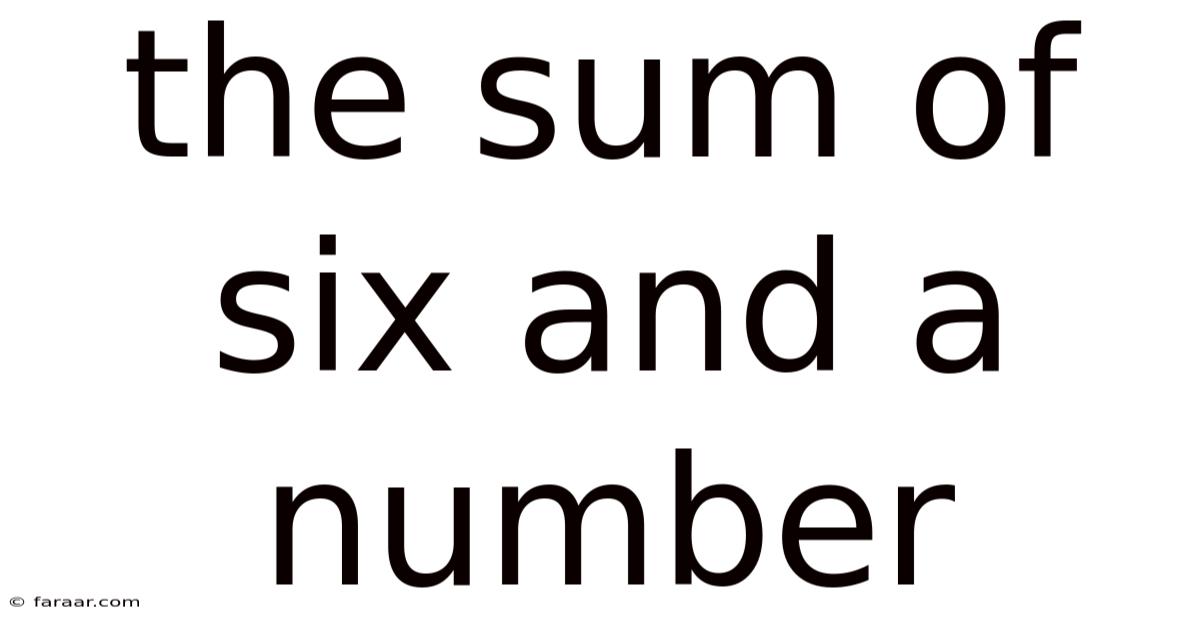
Table of Contents
Understanding the Sum of Six and a Number: A Comprehensive Guide
This article explores the seemingly simple concept of "the sum of six and a number," delving far beyond its basic arithmetic definition. We'll unpack its meaning, explore its applications in various mathematical contexts, and discuss its importance in developing fundamental mathematical reasoning. We'll cover everything from basic addition to more advanced algebraic manipulations, making it suitable for students of all levels, from elementary school to high school and beyond. Understanding this seemingly simple concept is crucial for building a solid foundation in mathematics.
What is the Sum of Six and a Number?
At its core, the "sum of six and a number" simply means the result of adding the number 6 to another number. This "another number" is often represented by a variable, typically x or n. Therefore, the expression can be written algebraically as: 6 + x or 6 + n. The sum itself is the answer you obtain after performing this addition. For example:
- If x = 4, then the sum of six and x is 6 + 4 = 10
- If n = 15, then the sum of six and n is 6 + 15 = 21
- If x = -2, then the sum of six and x is 6 + (-2) = 4
Exploring Different Mathematical Contexts
While seemingly straightforward, the expression "6 + x" unlocks numerous possibilities within different mathematical frameworks. Let's explore some of these:
1. Elementary Arithmetic: Building Blocks of Addition
For young learners, understanding the sum of six and a number is a fundamental step in mastering basic addition. It helps them grasp the concept of combining quantities and visualizing the process of addition. Through various exercises involving concrete objects (like blocks or counters), they can physically represent the addition of six to different numbers, strengthening their understanding of numerical relationships. This foundational knowledge is essential for tackling more complex arithmetic problems in the future.
2. Algebra: Introducing Variables and Equations
In algebra, the expression 6 + x becomes a crucial stepping stone towards understanding variables and equations. The variable x represents an unknown quantity, and the expression itself represents a relationship between numbers. We can use this expression to construct equations. For example:
- 6 + x = 12 This equation asks: "What number, when added to 6, equals 12?" Solving this requires subtracting 6 from both sides, resulting in x = 6.
- 6 + x = y This equation introduces another variable, y, showing how the sum of 6 and x can be equal to any other number. This highlights the versatility of algebraic expressions.
3. Functions and Mapping: Introducing the Concept of Input and Output
The expression 6 + x can be considered a simple function. We can think of x as the input, and the sum (6 + x) as the output. This introduces the concept of input-output relationships, which are fundamental to understanding functions in higher-level mathematics. For each input value of x, the function produces a corresponding output value. This functional representation lays the groundwork for more complex function analysis.
4. Word Problems and Real-World Applications
The phrase "the sum of six and a number" frequently appears in word problems, forcing students to translate real-world scenarios into mathematical expressions. Examples include:
- "John has 6 apples, and he receives x more apples from his friend. How many apples does John have in total?" This translates directly to the expression 6 + x.
- "A baker sells 6 loaves of bread in the morning, and x loaves in the afternoon. What is the total number of loaves sold?" This again becomes 6 + x.
These examples demonstrate the practical application of this seemingly simple concept in everyday situations.
5. Inequalities: Extending the Concept Beyond Equations
The concept extends beyond equations. We can use the expression "6 + x" in inequalities. For instance:
- 6 + x > 10 This inequality states that the sum of 6 and x is greater than 10. Solving this involves subtracting 6 from both sides, yielding x > 4. This means any number greater than 4 will satisfy the inequality.
- 6 + x ≤ 8 This inequality states that the sum of 6 and x is less than or equal to 8. Solving this gives x ≤ 2.
Step-by-Step Guide to Solving Equations Involving "6 + x"
Let's walk through solving equations that involve the expression "6 + x," progressively increasing in complexity:
Example 1: A Simple Equation
6 + x = 15
-
Isolate the variable: To solve for x, we need to isolate it on one side of the equation. We do this by subtracting 6 from both sides: 6 + x - 6 = 15 - 6
-
Simplify: This simplifies to: x = 9
Therefore, the solution is x = 9.
Example 2: An Equation with Negative Numbers
6 + x = -3
-
Isolate the variable: Subtract 6 from both sides: 6 + x - 6 = -3 - 6
-
Simplify: This simplifies to: x = -9
Therefore, the solution is x = -9.
Example 3: A More Complex Equation
2(6 + x) = 20
-
Distribute: First, distribute the 2 to both terms inside the parentheses: 12 + 2x = 20
-
Isolate the variable term: Subtract 12 from both sides: 2x = 8
-
Solve for x: Divide both sides by 2: x = 4
Therefore, the solution is x = 4.
Example 4: An Equation with Fractions
(6 + x)/3 = 5
-
Multiply both sides by 3: This eliminates the fraction: 6 + x = 15
-
Isolate the variable: Subtract 6 from both sides: x = 9
Therefore, the solution is x = 9.
The Significance of Understanding "6 + x"
The seemingly simple expression "6 + x" forms a cornerstone of mathematical understanding. Its mastery unlocks the ability to:
- Solve equations: This is a crucial skill in various mathematical fields and applications.
- Understand variables: Grasping the concept of variables is essential for advanced mathematical reasoning.
- Apply mathematical concepts to real-world problems: This allows for the practical application of theoretical knowledge.
- Develop problem-solving skills: Working with this expression enhances logical thinking and problem-solving abilities.
Frequently Asked Questions (FAQ)
Q: Can 'x' be any number, including decimals and fractions?
A: Yes, absolutely. x can represent any real number, including decimals, fractions, integers, and even irrational numbers like π (pi).
Q: What if the equation involves more than one variable?
A: If the equation involves more than one variable, you might not be able to find a single numerical solution for x. You would likely express x in terms of the other variable(s).
Q: Are there different ways to solve equations involving "6 + x"?
A: While the methods shown above are common and effective, there might be alternative approaches depending on the complexity of the equation. However, the core principle of isolating the variable remains consistent.
Q: How does understanding "6 + x" help in advanced mathematics?
A: This fundamental understanding builds the foundation for more complex concepts in algebra, calculus, and beyond. It helps in understanding functions, relationships between variables, and solving complex equations and inequalities.
Conclusion
The sum of six and a number, represented algebraically as 6 + x, is far more than a simple arithmetic expression. It serves as a gateway to understanding fundamental mathematical concepts, from basic addition to solving complex equations and inequalities. Mastering this seemingly simple concept is crucial for building a strong foundation in mathematics, empowering individuals to tackle more challenging problems and apply their knowledge to various real-world scenarios. Its importance should not be underestimated, as it forms the bedrock of many advanced mathematical principles. The continued practice and exploration of this expression will solidify mathematical understanding and pave the way for future success in the field.
Latest Posts
Latest Posts
-
How To Start A Paper With A Quote
Sep 18, 2025
-
Best Way To Use Uworld Mcat
Sep 18, 2025
-
Find The X Component Of This Vector
Sep 18, 2025
-
What Is 1 5 8 As A Decimal
Sep 18, 2025
-
Find The Most General Antiderivative Of The Function
Sep 18, 2025
Related Post
Thank you for visiting our website which covers about The Sum Of Six And A Number . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.