The Sum Of A Number And 6
faraar
Sep 23, 2025 · 6 min read
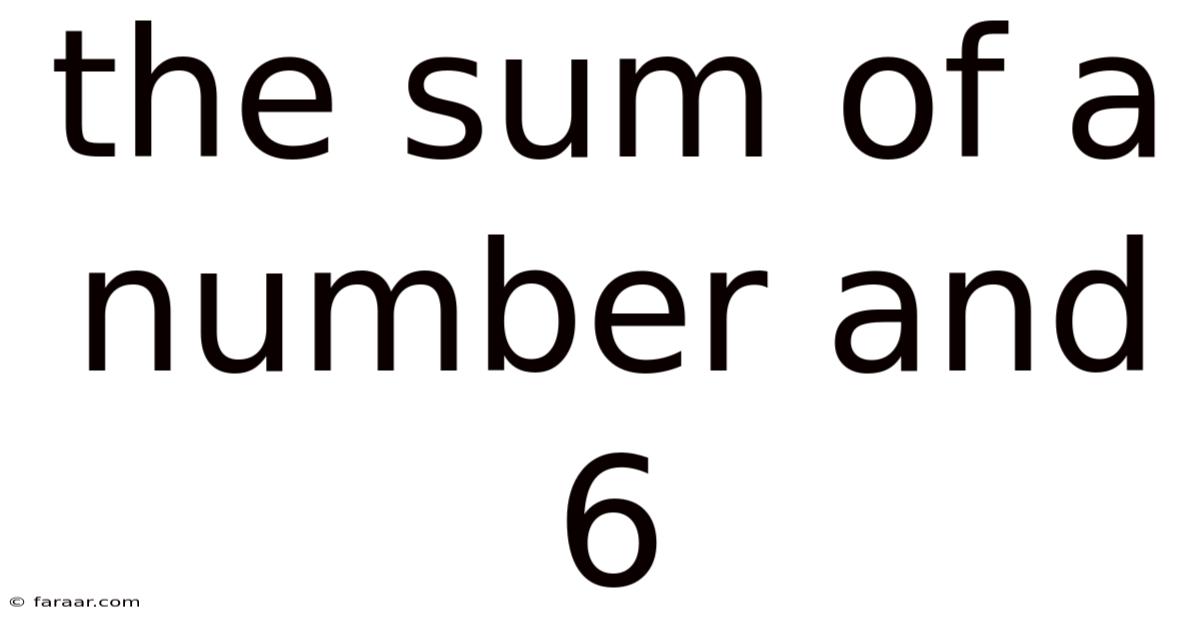
Table of Contents
Exploring the Sum of a Number and 6: A Deep Dive into Mathematical Concepts
This article delves into the seemingly simple concept of "the sum of a number and 6," unpacking its mathematical implications and exploring its applications across various mathematical fields. While the core concept is basic arithmetic, understanding its nuances opens doors to more complex algebraic concepts, problem-solving strategies, and even programming logic. We'll cover everything from basic addition to more advanced representations and applications, making it accessible to all levels of mathematical understanding. This exploration will include practical examples, real-world applications, and frequently asked questions, ensuring a comprehensive understanding of this fundamental mathematical operation.
Introduction: Understanding the Basics
At its heart, "the sum of a number and 6" is a straightforward addition problem. We're taking an unknown number (let's call it 'x') and adding 6 to it. This can be represented algebraically as x + 6. This simple expression forms the foundation for numerous mathematical concepts. It's the building block for understanding variables, equations, and the fundamental principles of algebra. Mastering this seemingly simple concept provides a crucial stepping stone towards more advanced mathematical learning.
Representing the Sum: Algebraic Expressions and Equations
The expression x + 6 is an algebraic expression. It combines a variable (x), representing an unknown number, with a constant (6). The "+" symbol indicates the operation of addition. This expression doesn't provide a specific numerical answer; it's a general representation applicable to any value of x.
To find a specific numerical answer, we need an equation. An equation equates an expression to a value. For example, x + 6 = 10 is an equation. Solving this equation involves finding the value of x that makes the equation true. In this case, subtracting 6 from both sides gives us x = 4. This means that when the unknown number is 4, the sum of that number and 6 is indeed 10.
Different types of equations can involve the expression x + 6. We can have simple linear equations like those mentioned above, or more complex equations involving multiple variables or operations.
Solving Equations Involving x + 6: Techniques and Strategies
Solving equations involving x + 6 utilizes basic algebraic manipulation. The core principle is to isolate the variable (x) by performing the same operation on both sides of the equation to maintain balance.
1. Simple Linear Equations:
Let's look at a few examples:
- x + 6 = 15: Subtract 6 from both sides: x = 15 - 6 = 9.
- x + 6 = -2: Subtract 6 from both sides: x = -2 - 6 = -8.
- x + 6 = 0: Subtract 6 from both sides: x = 0 - 6 = -6.
2. Equations with More Complex Operations:
Things get slightly more involved when other operations are present:
- 2(x + 6) = 20: First, distribute the 2: 2x + 12 = 20. Then, subtract 12 from both sides: 2x = 8. Finally, divide both sides by 2: x = 4.
- x + 6 + 3x = 16: Combine like terms: 4x + 6 = 16. Subtract 6 from both sides: 4x = 10. Divide both sides by 4: x = 2.5.
These examples illustrate the importance of order of operations (PEMDAS/BODMAS) and the consistent application of inverse operations to isolate the variable.
Visualizing the Sum: Number Lines and Graphs
Visual representations can greatly aid understanding. A number line provides a simple way to visualize adding 6 to a number. Start at the point representing 'x' on the number line, and then move 6 units to the right (for positive 6) to arrive at the sum. For negative values of x, you would start at the negative point and still move 6 units to the right.
Graphically, the expression x + 6 represents a linear function. Plotting the equation y = x + 6 results in a straight line with a slope of 1 and a y-intercept of 6. Each point (x, y) on the line represents a pair of values where y is the sum of x and 6.
Real-World Applications of x + 6
The concept of adding 6 to a number, seemingly simple, has various practical applications:
- Everyday Calculations: Adding 6 to the number of apples you have to determine the total number of apples after receiving 6 more.
- Business and Finance: Calculating profits after adding a fixed cost of 6 units to the production cost.
- Physics and Engineering: In some physics problems, adding a constant force (represented by 6) to an initial force to determine the net force.
- Programming: The expression x + 6 forms the basis of many programming algorithms. It can be used in loops, calculations, and data manipulation.
Expanding the Concept: Generalization and Abstraction
The concept of "the sum of a number and 6" can be generalized to "the sum of a number and a," where 'a' is any constant. This generalization highlights the fundamental principle of addition and its application to a broader range of numbers. This abstraction is a key element in abstract algebra and higher mathematical studies. It allows for the exploration of mathematical properties independently of specific numerical values.
Beyond Basic Addition: Exploring Related Mathematical Concepts
The simple concept of x + 6 touches upon several interconnected mathematical concepts:
- Inverse Operations: Subtraction is the inverse operation of addition. Solving x + 6 = 10 utilizes the inverse operation of subtracting 6 from both sides.
- Linear Equations: Equations of the form x + 6 = c (where c is a constant) are linear equations, the foundation of linear algebra.
- Functions: The expression x + 6 can be represented as a linear function, f(x) = x + 6, mapping input values (x) to output values (f(x)).
- Number Systems: The concept applies to all number systems, whether integers, real numbers, or complex numbers.
Frequently Asked Questions (FAQ)
Q1: What if x is a negative number?
A1: The process remains the same. For example, if x = -3, then x + 6 = -3 + 6 = 3. You would simply add 6 to the negative value of x.
Q2: Can x be a decimal or a fraction?
A2: Absolutely! The concept applies to all real numbers. For example, if x = 2.5, then x + 6 = 2.5 + 6 = 8.5. If x = 1/2, then x + 6 = 1/2 + 6 = 13/2 or 6.5.
Q3: How can I check my answer when solving an equation?
A3: Substitute the value you found for x back into the original equation. If the equation holds true, your answer is correct. For example, if you found x = 3 for the equation x + 6 = 9, substitute 3 for x: 3 + 6 = 9. Since this is true, your solution is correct.
Q4: What are some advanced applications of this concept?
A4: This seemingly simple concept forms the building blocks for complex mathematical concepts in fields like calculus, linear algebra, and differential equations. Understanding this foundation makes tackling those advanced topics much easier.
Conclusion: The Significance of Simplicity
While seemingly trivial, understanding "the sum of a number and 6" is a fundamental building block in mathematics. It lays the groundwork for more complex concepts, problem-solving techniques, and applications across diverse fields. Mastering this concept isn't just about getting the right answer; it's about grasping the underlying principles of algebra, equations, and mathematical reasoning. The journey from simple addition to the broader applications showcases the power of fundamental mathematical concepts and their significance in our understanding of the world around us. It's a testament to how even the simplest ideas can have profound implications in mathematics and beyond.
Latest Posts
Latest Posts
-
Handwriting Classes For Adults Near Me
Sep 23, 2025
-
Cos 4x Sin 4x Cos 2x
Sep 23, 2025
-
Line A Is Parallel To Line B
Sep 23, 2025
-
Find The Slope Of A Line Perpendicular
Sep 23, 2025
-
What Is The Measure Of Angle Dfe
Sep 23, 2025
Related Post
Thank you for visiting our website which covers about The Sum Of A Number And 6 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.