Cos 4x Sin 4x Cos 2x
faraar
Sep 23, 2025 · 6 min read
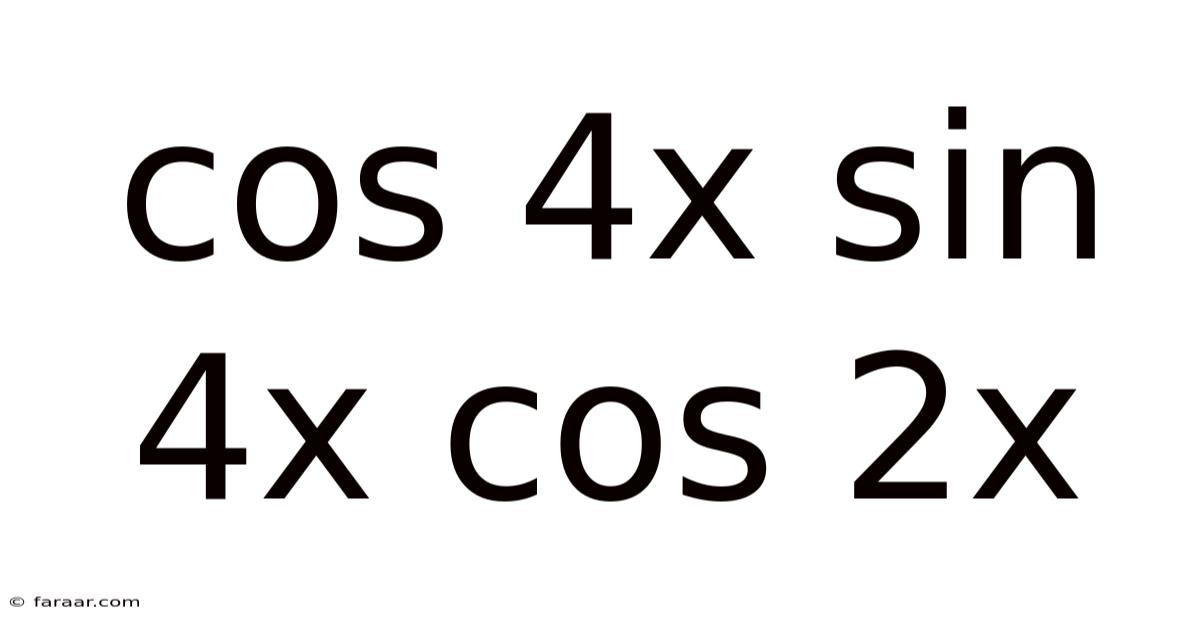
Table of Contents
Decomposing and Simplifying the Trigonometric Expression: cos 4x sin 4x cos 2x
This article delves into the simplification and decomposition of the trigonometric expression cos 4x sin 4x cos 2x. We will explore various methods to manipulate this expression, ultimately aiming to express it in a simpler, more manageable form. Understanding this process is crucial for various applications in mathematics, physics, and engineering, particularly in areas involving wave phenomena, oscillations, and signal processing. This comprehensive guide will provide a step-by-step approach, explaining the underlying trigonometric identities and offering insights into the broader context of trigonometric simplification.
Introduction
The trigonometric expression cos 4x sin 4x cos 2x presents a seemingly complex arrangement of trigonometric functions. However, by strategically applying trigonometric identities, we can significantly simplify this expression. Our primary goal is to reduce the expression to a form that is easier to analyze, differentiate, integrate, or use in other mathematical operations. This will involve leveraging fundamental identities like double-angle formulas, product-to-sum formulas, and potentially power-reducing formulas. The process itself serves as an excellent exercise in mastering trigonometric manipulation.
Method 1: Using the Product-to-Sum Formula
One effective approach to simplifying cos 4x sin 4x cos 2x involves employing the product-to-sum formula. This formula allows us to transform the product of two trigonometric functions into a sum or difference of trigonometric functions. The relevant product-to-sum formula is:
sin A cos B = ½ [sin(A + B) + sin(A - B)]
In our case, let A = 4x and B = 2x. Applying this to the first two terms, cos 4x sin 4x, we get:
cos 4x sin 4x = ½ [sin(4x + 4x) + sin(4x - 4x)] = ½ [sin 8x + sin 0] = ½ sin 8x
Now, substitute this back into the original expression:
cos 4x sin 4x cos 2x = (½ sin 8x) cos 2x
We can then use the product-to-sum formula again:
sin A cos B = ½ [sin(A + B) + sin(A - B)]
Here, A = 8x and B = 2x:
(½ sin 8x) cos 2x = ½ * ½ [sin(8x + 2x) + sin(8x - 2x)] = ¼ [sin 10x + sin 6x]
Therefore, the simplified expression becomes:
cos 4x sin 4x cos 2x = ¼ [sin 10x + sin 6x]
Method 2: Using Double-Angle Formulas
Another approach leverages the double-angle formulas. The double-angle formula for sine is:
sin 2A = 2 sin A cos A
We can rewrite our original expression as:
cos 4x sin 4x cos 2x = (cos 4x sin 4x) cos 2x
Now, notice that cos 4x sin 4x resembles half of the double-angle formula for sin 8x. We can rewrite it as:
cos 4x sin 4x = ½ (2 cos 4x sin 4x) = ½ sin 8x
Substituting this back into the original expression:
cos 4x sin 4x cos 2x = (½ sin 8x) cos 2x
Now, we can use the product-to-sum formula as in Method 1, ultimately arriving at the same simplified expression:
cos 4x sin 4x cos 2x = ¼ [sin 10x + sin 6x]
Method 3: Using the Product-to-Sum and Double Angle Formula Combined
This method combines the strengths of both previous methods for a more efficient solution. We start by utilizing the double angle formula for sine:
2 sin A cos A = sin 2A
We can rewrite our expression as:
cos 4x sin 4x cos 2x = (1/2) (2 sin 4x cos 4x) cos 2x = (1/2) sin 8x cos 2x
Now, we use the product to sum formula:
sin A cos B = 1/2 [sin(A+B) + sin(A-B)]
Letting A = 8x and B = 2x, we get:
(1/2) sin 8x cos 2x = (1/2) * (1/2) [sin(8x + 2x) + sin(8x - 2x)] = (1/4) [sin 10x + sin 6x]
Therefore, we again arrive at the simplified form:
cos 4x sin 4x cos 2x = ¼ [sin 10x + sin 6x]
Explanation of the Steps and Underlying Principles
The simplification process relies heavily on the fundamental trigonometric identities. The product-to-sum formulas are particularly crucial, allowing us to convert products of trigonometric functions into sums or differences. This conversion is beneficial because sums and differences are often easier to manipulate algebraically than products. The double-angle formulas are also instrumental in reducing the complexity of the expression. These formulas relate trigonometric functions of double angles (e.g., 2x, 4x, 8x) to functions of the original angle (x).
Applications and Further Exploration
The simplified expression, ¼ [sin 10x + sin 6x], finds applications in various fields. For instance, in signal processing, this form might represent the superposition of two sinusoidal waves with different frequencies (10x and 6x). In physics, it could model the combined effect of two oscillating systems. The process of simplification itself highlights the power and elegance of trigonometric identities in manipulating and solving complex mathematical problems.
Further exploration could involve investigating the behavior of this expression for specific values of x, graphing its function, or integrating it to find its antiderivative. Understanding its behavior across different intervals could also be a worthwhile pursuit. Exploring its relationship to other trigonometric expressions or exploring different methods of simplification could provide further insight.
Frequently Asked Questions (FAQ)
Q: Are there other methods to simplify this expression?
A: While the methods described above are efficient, other approaches might exist. One could explore the use of complex exponentials (Euler's formula) to simplify the expression. This method often provides a more concise solution, particularly for more complex trigonometric expressions.
Q: Why is it important to simplify trigonometric expressions?
A: Simplifying trigonometric expressions makes them easier to work with. This is crucial for calculus operations (differentiation and integration), solving equations, and applying them to real-world problems in fields like physics and engineering where trigonometric functions frequently represent wave phenomena.
Q: Can this simplified expression be further simplified?
A: The simplified form, ¼ [sin 10x + sin 6x], is considered relatively simple and is in a standard form suitable for many applications. While you might be able to express it differently using other trigonometric identities, it's unlikely to lead to a substantially simpler or more useful form.
Q: What if the expression was different, say cos 3x sin 2x cos x?
A: The approach would be similar. You would again use a combination of product-to-sum and possibly double-angle formulas strategically to simplify the expression. The specific identities used would depend on the specific arrangement of trigonometric functions.
Conclusion
Simplifying the trigonometric expression cos 4x sin 4x cos 2x demonstrates the power of applying fundamental trigonometric identities. Through a systematic application of the product-to-sum and double-angle formulas, we successfully reduced the expression to a much simpler form: ¼ [sin 10x + sin 6x]. This process underscores the importance of mastering trigonometric identities for solving complex mathematical problems and highlights their application in various fields, including signal processing and physics. The ability to manipulate and simplify such expressions is a cornerstone of mathematical proficiency and is crucial for advanced mathematical study. This exercise serves as a testament to the interconnectedness and elegance inherent in the world of trigonometry. The different methods presented offer flexibility and highlight the versatility of trigonometric identities in achieving simplification. Remember that practice and familiarity with these identities are key to mastering these techniques.
Latest Posts
Latest Posts
-
How Many 1 2 Cups Make 3 4 Cup
Sep 23, 2025
-
What Is 1 And 2 3 Cups Doubled
Sep 23, 2025
-
Which Graph Represents A Function With An Initial Value Of
Sep 23, 2025
-
How Do You Say Ice Cream In German
Sep 23, 2025
-
60 Of What Number Is 30
Sep 23, 2025
Related Post
Thank you for visiting our website which covers about Cos 4x Sin 4x Cos 2x . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.