The Sum Of 9 And A Number
faraar
Sep 17, 2025 · 6 min read
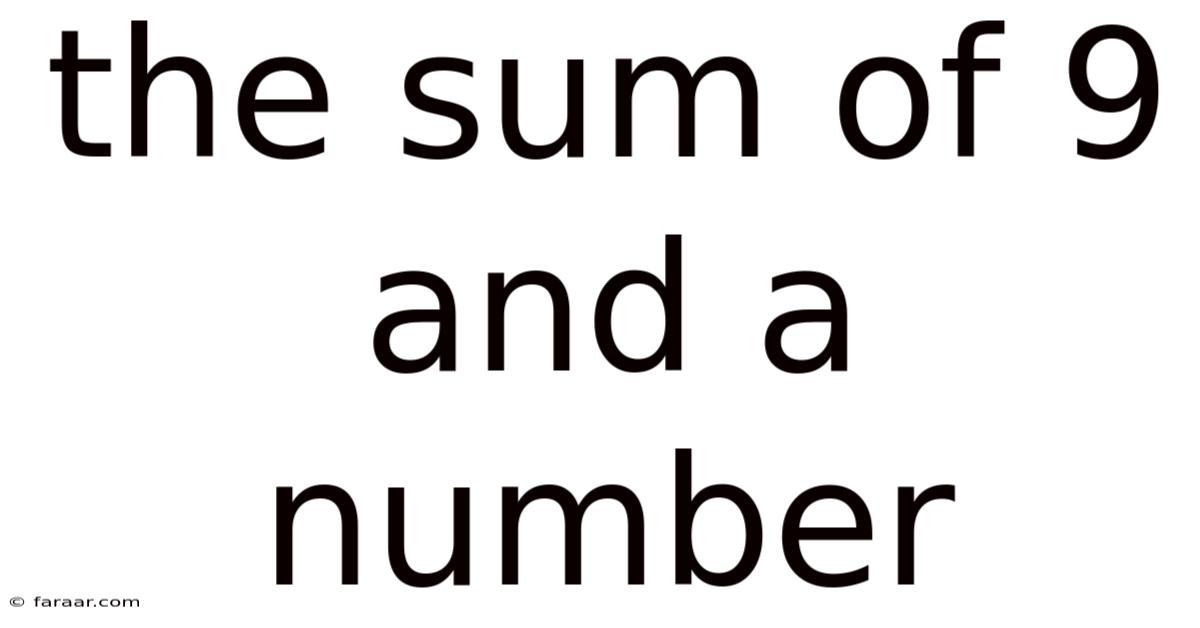
Table of Contents
Exploring the Sum of 9 and a Number: A Deep Dive into Addition and its Applications
The seemingly simple concept of "the sum of 9 and a number" opens a gateway to a vast world of mathematical exploration. This seemingly basic arithmetic operation forms the foundation for more complex algebraic concepts, problem-solving strategies, and even real-world applications. This article will delve into this seemingly simple concept, examining its implications across various mathematical disciplines and providing practical examples to solidify understanding. We will cover everything from basic addition to more advanced applications, ensuring a comprehensive understanding for readers of all levels.
Understanding the Fundamentals: Addition and Variables
At its core, "the sum of 9 and a number" represents an addition problem. Addition is one of the four fundamental arithmetic operations, combining two or more quantities to find their total. In this case, one quantity is a constant (9), and the other is a variable – a number that can take on various values. We typically represent this variable with a letter, such as x, y, or n. Therefore, the expression "the sum of 9 and a number" can be mathematically represented as:
9 + n
Where 'n' represents the unknown number. This simple expression forms the basis for much more complex mathematical concepts.
Exploring Different Representations: Equations and Expressions
It's crucial to distinguish between an expression and an equation. 9 + n is an algebraic expression. It represents a mathematical phrase containing numbers, variables, and operations. It doesn't state a relationship or equality. To make it an equation, we need to introduce an equals sign (=) and a value. For example:
9 + n = 15
This is now an equation. It states that the sum of 9 and an unknown number (n) is equal to 15. Solving this equation involves finding the value of n that makes the statement true. In this case, n = 6 (because 9 + 6 = 15).
Solving for the Unknown: Techniques and Strategies
Solving equations like 9 + n = 15 is a fundamental skill in algebra. The most common method is to use the inverse operation. Since addition is used in the equation, we use subtraction to isolate the variable. To solve for n, we subtract 9 from both sides of the equation:
9 + n - 9 = 15 - 9
This simplifies to:
n = 6
This process remains consistent regardless of the value on the right-hand side of the equation. If the equation were 9 + n = 22, we would still subtract 9 from both sides, yielding n = 13.
Beyond Basic Equations: Introducing More Complex Scenarios
The concept extends beyond simple equations. Consider scenarios involving multiple operations or variables. For example:
-
2(9 + n) = 30: This equation involves both addition and multiplication. We first need to simplify the expression within the parentheses before solving for n. Dividing both sides by 2 gives us 9 + n = 15, which we've already solved.
-
9 + n + m = 20: This equation introduces a second variable, m. We can't solve for a single value of n without knowing the value of m. We might need additional information or an additional equation to solve this completely.
Real-World Applications: Connecting Math to Everyday Life
The concept of "the sum of 9 and a number" isn't confined to abstract mathematical exercises. It has numerous practical applications in various aspects of daily life:
-
Shopping: If you have $9 and want to buy an item, you need to know the item's price to determine if you have enough money. The calculation involves adding 9 (your money) to a number (the remaining amount needed).
-
Cooking: A recipe calls for 9 ounces of flour, and you want to double the recipe. You need to add 9 ounces to 9 ounces to find the total amount of flour required.
-
Finance: Calculating your total savings if you already have $9 and then add a certain amount to your account involves the same principle.
-
Measurement: If a board measures 9 inches, and you need a total length of a certain amount, the calculation involves adding 9 to the needed additional length.
-
Construction: A worker has completed 9 units of a project and needs to know the sum to find total completion with the remaining amount.
Expanding the Concept: Patterns and Sequences
The concept can also be explored within the context of number patterns and sequences. For example, consider a sequence where each term is the sum of 9 and the previous term. Starting with 1, the sequence would be:
1, 10, 19, 28, 37...
Identifying patterns and understanding the underlying rules governing such sequences is crucial in various mathematical applications, including data analysis and prediction.
Advanced Applications: Functions and Linear Equations
"The sum of 9 and a number" can be represented as a function. A function is a relationship between inputs and outputs. In this case, the input is the number (n), and the output is the sum (9 + n). This can be written as:
f(n) = 9 + n
This functional representation allows us to explore the behavior of the sum for different values of n systematically. It also forms a basis for understanding linear equations, where the relationship between variables is represented by a straight line on a graph. The graph of f(n) = 9 + n would be a straight line with a slope of 1 and a y-intercept of 9.
Frequently Asked Questions (FAQ)
Q1: What if the number is negative?
A1: The concept remains the same. If the number is negative, you simply add it to 9. For example, the sum of 9 and -3 is 9 + (-3) = 6.
Q2: Can the sum of 9 and a number ever be negative?
A2: Yes, if the number is less than -9. For example, 9 + (-10) = -1.
Q3: How do I solve equations involving fractions or decimals?
A3: The principles remain the same. Use inverse operations to isolate the variable. You might need to perform additional steps to handle fractions or decimals appropriately.
Q4: What if the equation is more complicated?
A4: More complex equations may involve multiple variables or operations. Employ order of operations (PEMDAS/BODMAS) and isolate the variable systematically using inverse operations.
Q5: Where can I find more resources to learn about this?
A5: Many online resources, textbooks, and educational videos cover algebraic equations and solving techniques.
Conclusion: A Foundation for Mathematical Growth
The seemingly simple concept of "the sum of 9 and a number" serves as a powerful foundation for understanding more complex mathematical ideas. From basic addition to advanced algebraic manipulations and real-world applications, the principles explored here provide a solid base for further mathematical learning and problem-solving. By grasping the fundamental concepts of variables, equations, and inverse operations, individuals can build a strong foundation for success in mathematics and related fields. The journey from a simple sum to complex equations demonstrates the beauty and interconnectedness of mathematical concepts. Continuous exploration and practice are key to mastering these fundamentals and unlocking the potential for more advanced mathematical understanding.
Latest Posts
Latest Posts
-
How To Make A Dashed Line In Autocad
Sep 17, 2025
-
Can One Input Have Two Outputs
Sep 17, 2025
-
Is C2h5nh2 An Acid Or Base
Sep 17, 2025
-
What Is The Probability Of Rolling Doubles With Two Dice
Sep 17, 2025
-
Dilation By A Scale Factor Of 3
Sep 17, 2025
Related Post
Thank you for visiting our website which covers about The Sum Of 9 And A Number . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.