The Sum Of 5 Consecutive Even Numbers Is 200 .
faraar
Aug 29, 2025 · 5 min read
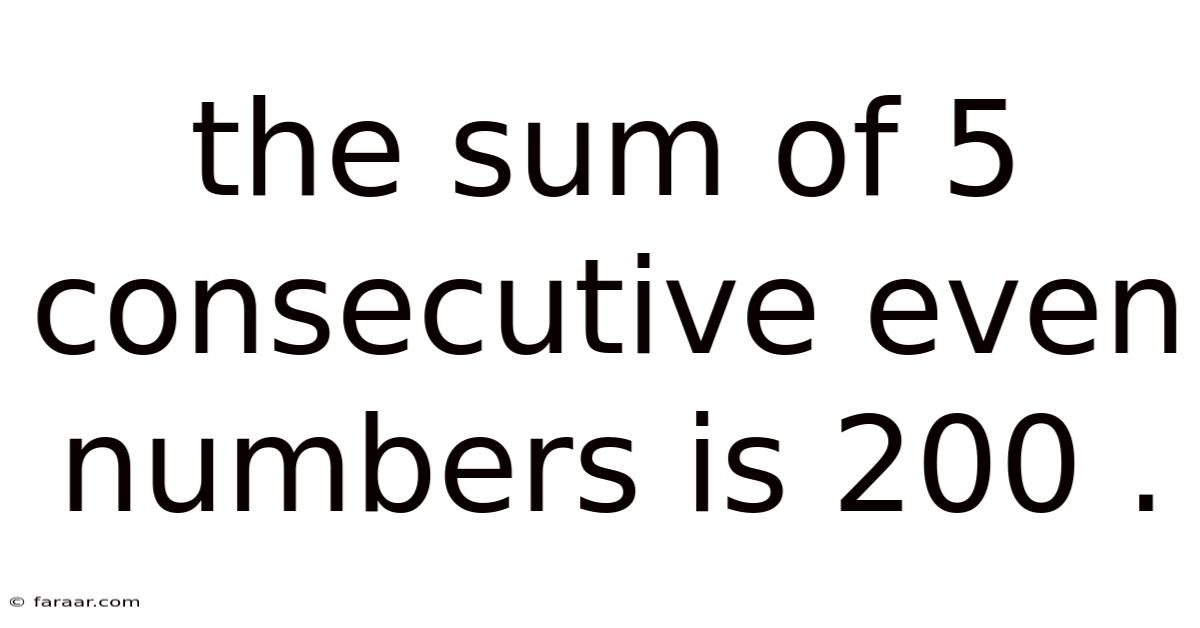
Table of Contents
The Sum of 5 Consecutive Even Numbers is 200: Unpacking the Math
Finding the solution to the problem "the sum of 5 consecutive even numbers is 200" might seem simple at first glance. However, this seemingly straightforward question offers a fantastic opportunity to explore several mathematical concepts, from basic arithmetic to algebraic problem-solving and even the beginnings of number theory. This article will walk you through different methods of solving this problem, delve into the underlying mathematical principles, and explore related concepts to provide a comprehensive understanding.
Understanding the Problem: Defining Consecutive Even Numbers
Before we dive into the solutions, let's clarify the terms. "Consecutive even numbers" means a sequence of even numbers that follow each other directly. For example, 2, 4, 6, 8, 10 are consecutive even numbers. The key is that each number is two more than the preceding number.
Method 1: The Arithmetic Approach
The most intuitive way to solve this is through trial and error, guided by arithmetic reasoning. We know the sum is 200, and we're dealing with five numbers. A rough estimate would be 200 / 5 = 40. This suggests that the numbers should be around 40. Since we need even numbers, we can try a sequence centered around 40:
Let's test the sequence: 36, 38, 40, 42, 44. Adding these numbers together: 36 + 38 + 40 + 42 + 44 = 200. Success! We've found our solution.
While this method is quick and effective for simple problems, it's not always practical for more complex scenarios involving larger numbers or more terms.
Method 2: The Algebraic Approach
Algebra provides a more robust and generalizable method. Let's represent the five consecutive even numbers algebraically. We can denote the first even number as 'x'. The subsequent even numbers would then be: x + 2, x + 4, x + 6, and x + 8.
The sum of these five consecutive even numbers is given as 200. Therefore, we can write an equation:
x + (x + 2) + (x + 4) + (x + 6) + (x + 8) = 200
Simplifying the equation:
5x + 20 = 200
Subtracting 20 from both sides:
5x = 180
Dividing both sides by 5:
x = 36
Therefore, the first even number (x) is 36. The consecutive even numbers are 36, 38, 40, 42, and 44. This confirms our solution from the arithmetic approach. This algebraic method is far more powerful because it can be applied to any similar problem, regardless of the sum or the number of consecutive even numbers.
Method 3: Utilizing the Concept of Arithmetic Series
This problem can also be solved using the concept of an arithmetic series. An arithmetic series is a sequence of numbers where the difference between consecutive terms is constant (in this case, 2). The formula for the sum of an arithmetic series is:
S = n/2 * [2a + (n-1)d]
Where:
- S = the sum of the series (200 in this case)
- n = the number of terms (5 in this case)
- a = the first term (which we need to find)
- d = the common difference (2 in this case, since they are consecutive even numbers)
Plugging in the known values:
200 = 5/2 * [2a + (5-1)2]
200 = 5/2 * [2a + 8]
Multiplying both sides by 2/5:
80 = 2a + 8
Subtracting 8 from both sides:
72 = 2a
Dividing both sides by 2:
a = 36
Again, we find that the first term (a) is 36, leading to the same sequence of consecutive even numbers: 36, 38, 40, 42, 44.
Extending the Concept: Generalizing the Solution
Let's generalize the solution for finding the sum of 'n' consecutive even numbers. If we let the first even number be 'x', the sum can be represented as:
x + (x + 2) + (x + 4) + ... + (x + 2(n-1)) = S
This simplifies to:
nx + 2(1 + 2 + ... + (n-1)) = S
The sum of the series 1 + 2 + ... + (n-1) is given by the formula n(n-1)/2. Substituting this:
nx + n(n-1) = S
This equation allows us to solve for 'x' (the first even number) given any sum 'S' and number of consecutive even numbers 'n'. For example, if we had the sum of 7 consecutive even numbers equaling 252, we could plug in n=7 and S=252 to find x and subsequently the sequence.
Further Exploration: Odd Numbers and Other Sequences
The principles discussed here can be easily adapted to solve problems involving consecutive odd numbers or other arithmetic sequences. The only change needed would be to adjust the common difference ('d' in the arithmetic series formula) accordingly. For odd numbers, the common difference would be 2, just like for even numbers. The approach of using algebra to form and solve an equation remains the most powerful and versatile method for tackling such problems.
Frequently Asked Questions (FAQ)
-
Q: Can this be solved without algebra? A: Yes, for smaller numbers and fewer terms, trial and error or arithmetic reasoning can work. However, algebra provides a more efficient and reliable method for larger numbers and more terms.
-
Q: What if the sum wasn't 200? A: The algebraic method remains the same. You would simply substitute the new sum into the equation and solve for 'x'.
-
Q: What if we were dealing with consecutive odd numbers? A: The approach would be very similar. You'd just adjust the common difference in the arithmetic series formula to 2, and the algebraic expression would reflect the sequence of odd numbers instead of even numbers.
-
Q: Are there other ways to solve this? A: Yes, more advanced techniques in number theory could be applied, but the methods outlined above are sufficient and easily understandable for most.
Conclusion
The seemingly simple problem of finding five consecutive even numbers that sum to 200 provides a rich learning opportunity. We've explored several approaches, highlighting the power and versatility of algebra in solving mathematical problems. Understanding these methods not only helps solve this specific problem but equips you with the tools to tackle similar problems involving different sequences and sums, broadening your mathematical understanding and problem-solving skills. The journey from arithmetic trial-and-error to the generalized algebraic solution showcases the elegance and efficiency of mathematical thinking. Remember, the key is not just finding the answer, but understanding the underlying principles and developing the ability to apply them to a wider range of problems.
Latest Posts
Latest Posts
-
1 2 To The Negative 1 Power
Aug 29, 2025
-
14 Tens Is The Same As
Aug 29, 2025
-
What Is 33 And 1 3 As A Decimal
Aug 29, 2025
-
Which Of The Following Is The Conjugate Acid Of Nh2
Aug 29, 2025
-
Rotate 270 Degrees Counterclockwise About The Origin
Aug 29, 2025
Related Post
Thank you for visiting our website which covers about The Sum Of 5 Consecutive Even Numbers Is 200 . . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.