What Is 33 And 1/3 As A Decimal
faraar
Aug 29, 2025 · 5 min read
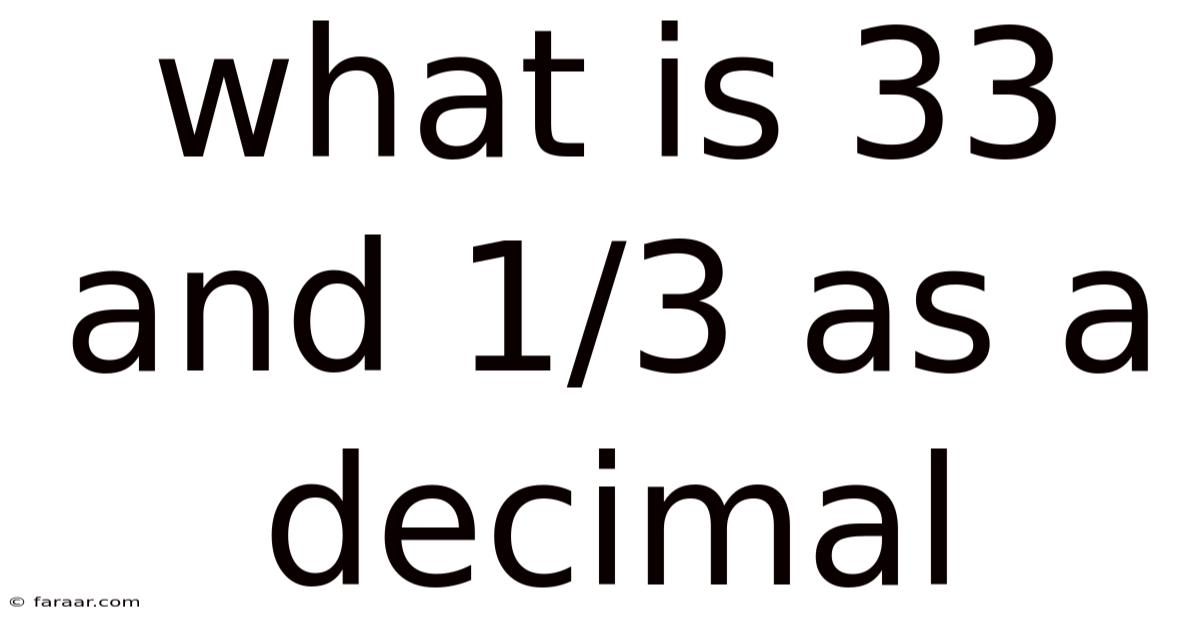
Table of Contents
Decoding 33 and 1/3 as a Decimal: A Comprehensive Guide
Understanding how to convert fractions to decimals is a fundamental skill in mathematics. This comprehensive guide will walk you through the process of converting the mixed number 33 and 1/3 into its decimal equivalent, explaining the method in detail and exploring the underlying mathematical principles. We'll also delve into why this seemingly simple conversion holds significance in various fields and address frequently asked questions. By the end, you'll not only know the answer but also understand the "why" behind the conversion, empowering you to tackle similar problems with confidence.
Understanding Mixed Numbers and Decimals
Before diving into the conversion, let's briefly review the concepts of mixed numbers and decimals. A mixed number combines a whole number and a fraction, like 33 and 1/3. A decimal, on the other hand, represents a number using a base-ten system, where digits to the right of the decimal point represent fractions of powers of ten (tenths, hundredths, thousandths, etc.).
Converting 33 and 1/3 to a Decimal: The Step-by-Step Process
The conversion process involves two main steps:
-
Converting the Fraction to a Decimal: The core of the problem lies in converting the fraction 1/3 to its decimal representation. To do this, we perform a simple division: 1 divided by 3.
This division results in a repeating decimal: 0.33333... The three repeats infinitely. This is often represented as 0.<u>3</u>, with the line above the 3 indicating the repeating nature.
-
Combining the Whole Number and Decimal Fraction: Now that we know the decimal equivalent of 1/3 (approximately 0.3333...), we simply add it to the whole number part of our mixed number:
33 + 0.3333... = 33.3333...
Therefore, 33 and 1/3 as a decimal is 33.3333... or 33.<u>3</u>.
Understanding Repeating Decimals
The result, 33.<u>3</u>, highlights an important characteristic of decimal representations: repeating decimals. Not all fractions convert to "neat" terminating decimals. Some produce decimals that repeat a sequence of digits infinitely. 1/3 is a classic example of this.
The reason for the repeating decimal arises from the nature of the division. When dividing 1 by 3, you'll find that no matter how many decimal places you calculate, you'll always have a remainder of 1, leading to the continuous repetition of the digit 3.
Practical Applications and Significance
While seemingly simple, understanding this conversion has significant implications in various fields:
-
Engineering and Construction: Precise measurements are crucial in these fields. Representing fractions as decimals allows for greater accuracy in calculations and blueprints. Understanding repeating decimals helps in estimating error margins.
-
Finance and Accounting: Calculations involving money often involve fractions (e.g., calculating interest rates or dividing profits). Converting fractions to decimals simplifies these calculations and improves the clarity of financial reports.
-
Science and Technology: Scientific data often includes measurements that need to be represented in decimal form for analysis and comparison. Accurate decimal representation is essential for consistent and reliable results.
-
Computer Programming: Computers primarily work with decimal representations of numbers. Understanding fraction-to-decimal conversions is vital for programmers to accurately handle numerical data and implement algorithms involving fractions.
-
Everyday Life: Even in everyday scenarios, understanding decimals is valuable. Sharing a pizza amongst friends, calculating discounts, or measuring ingredients for a recipe all involve fractions that are often better expressed as decimals for practical calculation.
Addressing Common Misconceptions
-
Rounding: While 33.3333... can be rounded to a specific number of decimal places (e.g., 33.33 or 33.3), it's crucial to understand that this introduces a degree of approximation. The precise value is the infinite repeating decimal.
-
Truncation: Truncating the decimal (simply cutting off the digits after a certain point) also introduces error. It's not as accurate as rounding, which at least considers the next digit before cutting.
-
Using Calculators: Calculators can help in the conversion, but they may display a rounded or truncated value instead of the true repeating decimal. Always be aware of the limitations of calculator displays when dealing with repeating decimals.
Frequently Asked Questions (FAQs)
Q1: Why does 1/3 result in a repeating decimal?
A1: Because 3 is not a factor of 10 (or any power of 10). When converting a fraction to a decimal, we essentially perform long division. If the denominator has prime factors other than 2 and 5 (the prime factors of 10), the decimal representation will repeat.
Q2: Is there a way to represent 33 and 1/3 exactly without using a repeating decimal?
A2: Yes, the mixed number 33 and 1/3 is the most accurate way to represent the value without approximation. The repeating decimal is simply an alternative representation, not inherently more or less accurate.
Q3: How many decimal places should I use when working with 33 and 1/3?
A3: It depends on the context. For everyday calculations, a few decimal places (e.g., 33.33) might suffice. However, for scientific or engineering applications requiring high precision, more decimal places might be necessary. In many instances, it's better to leave the answer in its exact fractional form (33 and 1/3) to avoid rounding errors.
Q4: Can all fractions be converted to decimals?
A4: Yes, all fractions can be converted to decimals. They will either result in a terminating decimal (a decimal that ends after a finite number of digits) or a repeating decimal (a decimal that repeats a sequence of digits infinitely).
Q5: How can I convert other fractions to decimals?
A5: The process is the same: divide the numerator by the denominator. If the division results in a remainder of 0, the decimal is terminating. If the division results in a repeating remainder, the decimal will be repeating.
Conclusion
Converting 33 and 1/3 to a decimal, resulting in 33.<u>3</u>, illustrates the fundamental concept of fraction-to-decimal conversion and the nature of repeating decimals. Understanding this process, along with its practical applications and limitations, equips you with a valuable mathematical skill applicable in various fields and everyday scenarios. Remember that while a rounded decimal can be useful in practical applications, the exact representation remains 33 and 1/3 or the infinitely repeating decimal 33.<u>3</u>. Choosing the best representation depends entirely on the context and the required level of precision.
Latest Posts
Latest Posts
-
2 Planes That Do Not Intersect
Aug 29, 2025
-
Ethanol Is Used In The Dna Isolation Process Because
Aug 29, 2025
-
Dramatic Description In The Fall Of The House Of Usher
Aug 29, 2025
-
Someone Who Is Good With Words
Aug 29, 2025
-
Geometry Postulates And Theorems List With Pictures
Aug 29, 2025
Related Post
Thank you for visiting our website which covers about What Is 33 And 1/3 As A Decimal . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.