Sec X Cos X Sin X
faraar
Sep 13, 2025 · 5 min read
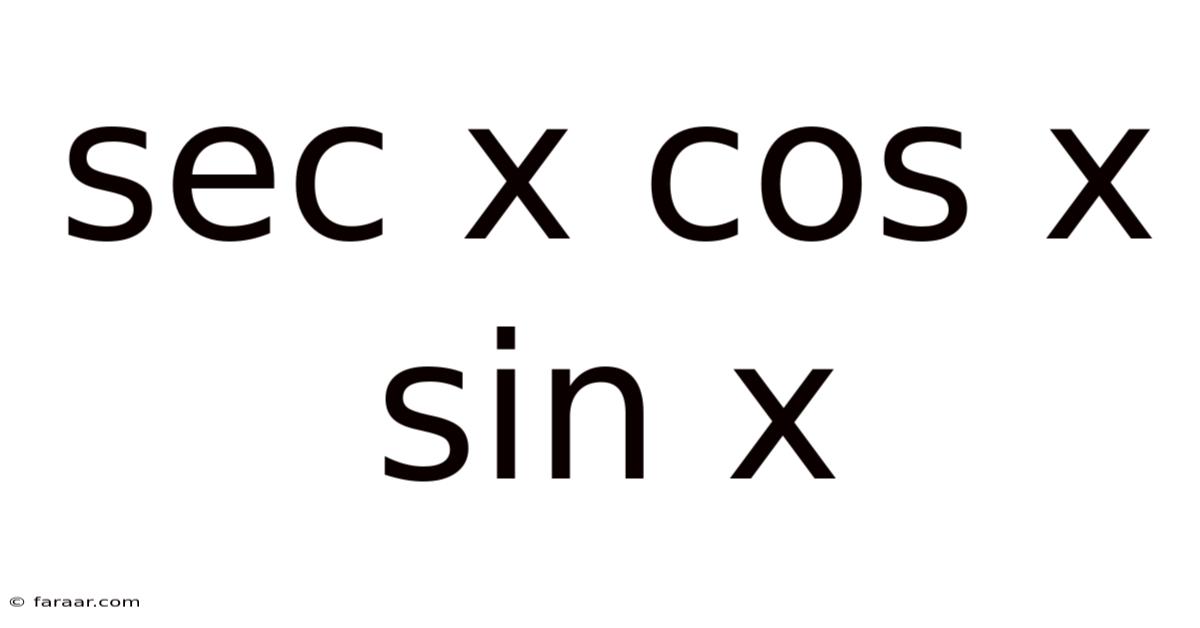
Table of Contents
Unveiling the Secrets of sec x cos x sin x: A Deep Dive into Trigonometric Identities
This article explores the trigonometric expression sec x cos x sin x, simplifying it, analyzing its properties, and examining its applications. Understanding this seemingly simple expression unlocks a deeper appreciation for trigonometric identities and their role in mathematics, physics, and engineering. We'll delve into the intricacies of the expression, providing a comprehensive guide suitable for students and anyone interested in strengthening their trigonometric knowledge. This exploration will cover simplification, graphical representation, applications, and frequently asked questions, ensuring a thorough understanding of the topic.
Understanding the Components: A Trigonometric Primer
Before diving into the simplification of sec x cos x sin x, let's refresh our understanding of the key trigonometric functions involved:
-
sec x (secant of x): The secant function is the reciprocal of the cosine function. Therefore,
sec x = 1/cos x. -
cos x (cosine of x): Cosine is a fundamental trigonometric function representing the ratio of the adjacent side to the hypotenuse in a right-angled triangle.
-
sin x (sine of x): Sine is another fundamental trigonometric function representing the ratio of the opposite side to the hypotenuse in a right-angled triangle.
Understanding these definitions is crucial for simplifying our target expression.
Simplifying sec x cos x sin x
Now, let's tackle the simplification of sec x cos x sin x. By substituting the definition of secant, we get:
(1/cos x) * cos x * sin x
Notice that cos x appears in both the numerator and the denominator. We can cancel these terms, provided cos x ≠ 0 (since division by zero is undefined). This simplification leaves us with:
sin x
Therefore, the simplified form of sec x cos x sin x is simply sin x, provided cos x ≠ 0. This crucial caveat highlights the importance of considering the domain of the function. The original expression is undefined whenever cos x = 0, which occurs at odd multiples of π/2 (e.g., π/2, 3π/2, 5π/2, etc.).
Graphical Representation and Analysis
Visualizing the function sin x helps solidify our understanding of the simplified expression. The graph of y = sin x is a periodic wave oscillating between -1 and 1. Its period is 2π, meaning the graph repeats itself every 2π units. The x-intercepts occur at multiples of π, while the maximum value (1) occurs at π/2 + 2kπ (where k is an integer) and the minimum value (-1) occurs at 3π/2 + 2kπ.
Comparing this graph to the original expression sec x cos x sin x, we observe that the graphs are identical except at the points where cos x = 0. At these points, sec x is undefined, resulting in the original expression being undefined as well. This reinforces the importance of the condition cos x ≠ 0.
Exploring the Implications: Applications in Various Fields
The simplification of sec x cos x sin x to sin x has implications across various fields:
-
Physics: In wave mechanics, the sine function is fundamental in describing oscillatory motion, including simple harmonic motion, wave propagation (sound, light), and alternating current (AC) circuits. The simplified expression allows for easier manipulation of equations describing these phenomena.
-
Engineering: Trigonometric functions are crucial in structural analysis, where angles and forces are key components. The simplification process helps engineers simplify complex calculations involving angles and forces. For instance, it can simplify calculations related to stress and strain analysis in structures.
-
Computer Graphics: Trigonometric functions are extensively used in computer graphics to model rotations, translations, and other transformations. Simplified expressions, such as
sin xderived from our original expression, facilitate efficient computational processes. -
Mathematics: This simplification exercise showcases the power of trigonometric identities and the importance of careful manipulation of expressions to achieve simpler, more manageable forms. It highlights the interconnectedness of different trigonometric functions and their relationships.
Further Exploration: Advanced Trigonometric Identities
Understanding the simplification of sec x cos x sin x opens doors to explore more complex trigonometric identities. For example, we can consider related expressions like:
-
sec x sin²x cos xwhich simplifies totan x sin x(provided cos x ≠ 0) -
sec²x cos x sin xwhich simplifies tosin x / cos² x = sin x sec²x(provided cos x ≠ 0)
These examples demonstrate how a simple understanding of fundamental identities can be used as a building block for solving more intricate trigonometric problems.
Frequently Asked Questions (FAQ)
Q1: Why is the condition cos x ≠ 0 important?
A1: The condition cos x ≠ 0 is crucial because the secant function (sec x = 1/cos x) is undefined when cos x = 0. Dividing by zero is an undefined mathematical operation. Therefore, the original expression sec x cos x sin x is undefined at points where cos x = 0.
Q2: Can this simplification be used to solve trigonometric equations?
A2: Yes, absolutely. If an equation involves the expression sec x cos x sin x, you can simplify it to sin x (with the condition cos x ≠ 0) to make the equation easier to solve. This simplification reduces the complexity and makes finding solutions more straightforward.
Q3: Are there other ways to simplify this expression?
A3: While the method presented here is the most straightforward and efficient, you could potentially use other trigonometric identities to arrive at the same result. However, the direct substitution of sec x = 1/cos x provides the most efficient path to simplification.
Q4: What is the practical significance of this simplification?
A4: The simplification reduces complexity, making further calculations and problem-solving significantly easier. This is especially useful in applications where trigonometric expressions are frequently encountered, such as physics, engineering, and computer graphics. It allows for more efficient computation and a clearer understanding of the underlying relationships between variables.
Conclusion: Mastering Trigonometric Simplification
This comprehensive exploration of sec x cos x sin x demonstrates the power of trigonometric identities and the importance of careful simplification. The seemingly simple expression reveals a deeper understanding of fundamental trigonometric functions, their relationships, and their applications in various fields. Remember the key takeaway: sec x cos x sin x simplifies to sin x, provided cos x ≠ 0. This seemingly small simplification can greatly aid in solving complex problems and offers a foundational understanding for tackling more advanced trigonometric concepts. By mastering these foundational concepts, you will be well-equipped to navigate the intricacies of trigonometry and its wide-ranging applications.
Latest Posts
Latest Posts
-
How To Find Net Change Between Two Points
Sep 13, 2025
-
Is Square Root Of 13 A Rational Number
Sep 13, 2025
-
Find The Value Of The Linear Correlation Coefficient R
Sep 13, 2025
-
P 2w 2l Solve For L
Sep 13, 2025
-
How To Start A Speech For Graduation
Sep 13, 2025
Related Post
Thank you for visiting our website which covers about Sec X Cos X Sin X . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.