P 2w 2l Solve For L
faraar
Sep 13, 2025 · 5 min read
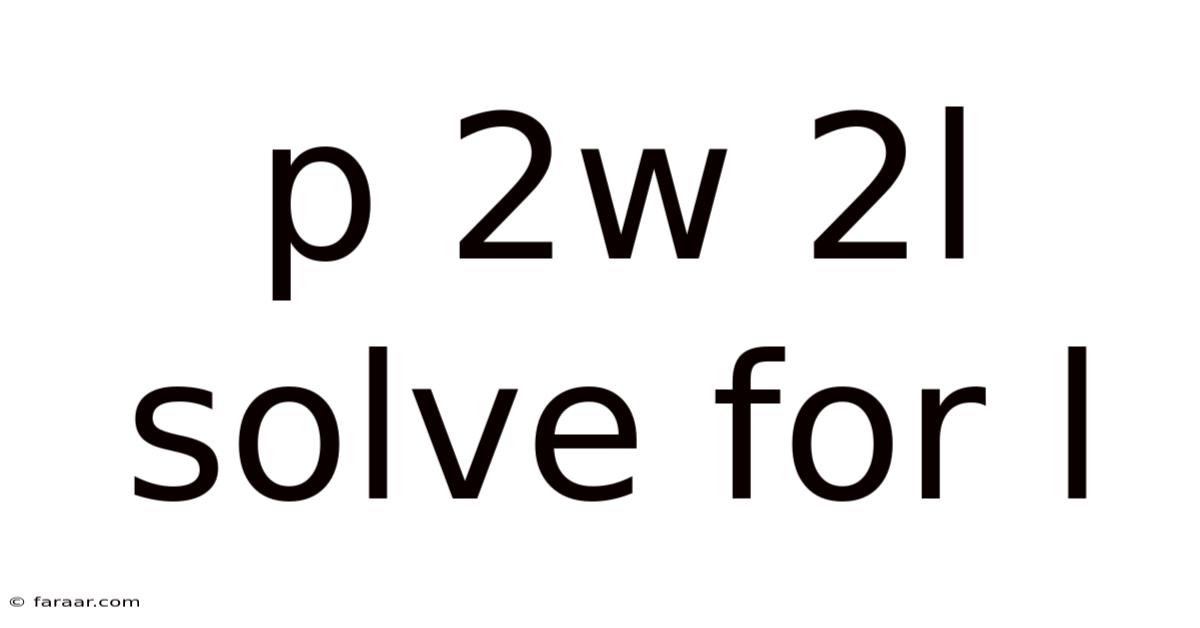
Table of Contents
Solving for 'l' in P = 2w + 2l: A Comprehensive Guide
This article provides a thorough explanation of how to solve for the variable 'l' (length) in the equation P = 2w + 2l, commonly used in calculating the perimeter of a rectangle. We'll cover the algebraic steps involved, provide practical examples, explore related concepts, and answer frequently asked questions to ensure a complete understanding. This guide is perfect for students learning algebra, geometry, or anyone needing to refresh their math skills related to solving for variables in equations. Understanding this fundamental equation is crucial for various applications, from calculating the fencing needed for a yard to solving more complex geometric problems.
Understanding the Equation: P = 2w + 2l
The equation P = 2w + 2l represents the formula for calculating the perimeter (P) of a rectangle. Let's break down each component:
- P: Represents the perimeter of the rectangle. The perimeter is the total distance around the outside of the rectangle.
- w: Represents the width of the rectangle. This is the shorter side of the rectangle.
- l: Represents the length of the rectangle. This is the longer side of the rectangle.
The equation states that the perimeter is equal to twice the width plus twice the length. This is because a rectangle has two pairs of equal sides.
Solving for 'l': Step-by-Step Guide
Our goal is to isolate 'l' on one side of the equation. To do this, we'll use basic algebraic principles. Here's a step-by-step guide:
Step 1: Subtract 2w from both sides of the equation.
This removes the '2w' term from the right side, bringing us closer to isolating 'l'. The equation becomes:
P - 2w = 2l
Step 2: Divide both sides of the equation by 2.
This isolates 'l', since dividing 2l by 2 gives us just 'l'. The equation now looks like this:
(P - 2w) / 2 = l
Step 3: Simplify (optional).
While the equation above is perfectly correct, we can often simplify it for easier use. We can distribute the division by 2:
l = P/2 - w
Therefore, the solution for 'l' is:
l = (P - 2w) / 2 or l = P/2 - w
Both equations are equivalent and correct; choose the one that feels more intuitive to you.
Practical Examples
Let's apply this formula to some real-world scenarios.
Example 1:
A rectangular garden has a perimeter of 20 meters and a width of 4 meters. What is the length of the garden?
- Identify the known variables: P = 20 meters, w = 4 meters.
- Substitute the values into the equation: l = (20 - 2 * 4) / 2
- Solve for l: l = (20 - 8) / 2 = 12 / 2 = 6 meters.
Therefore, the length of the garden is 6 meters.
Example 2:
A rectangular swimming pool has a perimeter of 36 feet and a length of 12 feet. What is the width of the pool?
In this case we already know the length and want to find the width. Let’s use the rearranged formula: w = P/2 - l
- Identify the known variables: P = 36 feet, l = 12 feet.
- Substitute the values into the equation: w = 36/2 - 12
- Solve for w: w = 18 - 12 = 6 feet.
Therefore, the width of the swimming pool is 6 feet.
Explanation with Scientific/Mathematical Background
The formula P = 2w + 2l is a direct application of the concept of perimeter in Euclidean geometry. A rectangle, by definition, possesses four sides with opposite sides being equal in length. This equality is the fundamental reason why the formula incorporates '2w' and '2l'. The derivation of the formula for 'l' involves basic algebraic manipulation, primarily using the properties of equality. Subtracting a term from both sides of an equation maintains the equality, and similarly, dividing both sides by a non-zero number also preserves the equality. These principles, central to algebra, are used to isolate 'l' and express it in terms of P and w.
The rearrangement of the formula into l = P/2 - w demonstrates the commutative property of addition and subtraction. The order in which we subtract doesn't change the result. This algebraic manipulation allows for easier calculation in some scenarios, especially when the perimeter and the length are known, and one needs to determine the width.
Frequently Asked Questions (FAQ)
Q1: What if I only know the perimeter and the length? How do I find the width?
A1: You can use the rearranged formula we derived: w = (P - 2l) / 2. Simply substitute the known values for P and l to solve for w.
Q2: Can this formula be used for other shapes?
A2: No, this formula specifically applies to rectangles. Other shapes, like squares (a special case of a rectangle where w=l), triangles, or circles, have different perimeter formulas.
Q3: What happens if I get a negative value for 'l' or 'w'?
A3: A negative value for length or width is not physically possible. If you obtain a negative result, it means there's an error in the input values or the calculations. Double-check your numbers and the steps you've taken.
Q4: Are there any alternative methods to solve for 'l'?
A4: While the algebraic method described is the most efficient, you could potentially use graphical methods or numerical methods (like iterative approximation) to find the value of 'l'. However, these methods are generally less efficient for this specific problem.
Q5: Why is understanding this equation important?
A5: Understanding this equation is fundamental for several reasons: it's a building block for more complex geometric problems, it teaches basic algebraic manipulation skills, and it has practical applications in various fields, from construction and design to surveying and even computer graphics.
Conclusion
Solving for 'l' in the equation P = 2w + 2l is a straightforward process involving basic algebraic manipulation. By understanding the steps involved and practicing with examples, you can confidently solve for any unknown variable within this equation. Remember the key steps: subtract 2w from both sides, then divide by 2 to isolate 'l'. This fundamental skill is valuable not just in geometry but also in developing a strong foundation in algebra and problem-solving. Mastering this seemingly simple equation unlocks the door to tackling more complex mathematical challenges in the future. Don't hesitate to practice and build your confidence – the more you practice, the easier it becomes!
Latest Posts
Latest Posts
-
Some People Exchanged For Cookies
Sep 13, 2025
-
Phosphate Express Your Answer As A Chemical Formula
Sep 13, 2025
-
How Do You Construct A 95 Confidence Interval
Sep 13, 2025
-
What Is The Most Electronegative Atom
Sep 13, 2025
-
Find 4 Consecutive Integers With The Sum Of 54
Sep 13, 2025
Related Post
Thank you for visiting our website which covers about P 2w 2l Solve For L . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.