Positive Number Divided By A Negative Number
faraar
Sep 20, 2025 · 6 min read
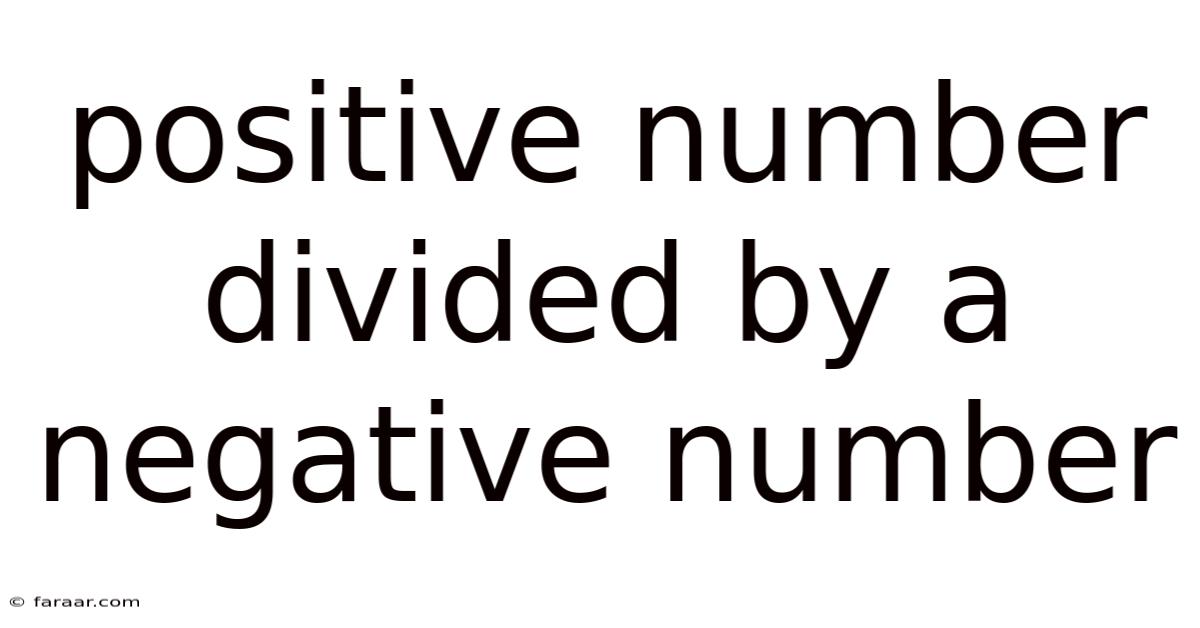
Table of Contents
Understanding the Division of Positive Numbers by Negative Numbers: A Comprehensive Guide
Dividing a positive number by a negative number is a fundamental concept in mathematics that often causes confusion for students. This comprehensive guide will break down the process step-by-step, explaining the underlying principles, providing practical examples, and addressing frequently asked questions. Understanding this concept is crucial for mastering more advanced mathematical operations and problem-solving. We'll explore why the result is always negative, the implications for real-world applications, and offer strategies to overcome common misconceptions.
Introduction: The Basics of Division
Division is essentially the inverse operation of multiplication. When we divide a number (the dividend) by another number (the divisor), we are essentially asking: "How many times does the divisor fit into the dividend?" For example, 12 ÷ 3 = 4 because 3 fits into 12 four times. This simple concept extends to include negative numbers, though the introduction of negative signs adds a layer of complexity.
The Rule: A Positive Divided by a Negative is Always Negative
The fundamental rule to remember is this: a positive number divided by a negative number always results in a negative number. This holds true regardless of the magnitude of the numbers involved.
Let's examine why this is the case. We can approach this from a few perspectives:
-
Multiplication as the Inverse: Remember that division is the inverse of multiplication. If we have the equation 6 ÷ (-2) = x, we can rewrite this as (-2) * x = 6. What number, when multiplied by -2, gives us 6? The answer is -3. Therefore, 6 ÷ (-2) = -3. This illustrates the inverse relationship and why a negative result is necessary.
-
Number Line Visualization: Imagine a number line. A positive number represents movement to the right, and a negative number represents movement to the left. Division by a negative number can be thought of as reversing the direction of movement. If we are dividing a positive number (movement to the right), dividing by a negative number reverses this direction to the left, resulting in a negative outcome.
-
Patterns and Consistency: Consider a series of divisions:
- 6 ÷ 2 = 3
- 6 ÷ 1 = 6
- 6 ÷ 0.5 = 12
- 6 ÷ 0.1 = 60
- 6 ÷ (-0.1) = -60
- 6 ÷ (-0.5) = -12
- 6 ÷ (-1) = -6
- 6 ÷ (-2) = -3
Notice the pattern. As the divisor approaches zero from the positive side, the quotient gets larger and larger. When the divisor becomes negative, the quotient becomes negative, maintaining a consistent relationship.
Step-by-Step Guide to Solving Problems
Solving problems involving the division of positive numbers by negative numbers is straightforward once you understand the core rule. Here's a step-by-step approach:
-
Identify the dividend and the divisor: Determine which number is being divided (dividend) and which number is doing the dividing (divisor).
-
Apply the rule: Remember that a positive divided by a negative is always negative.
-
Perform the division: Ignore the signs for now and perform the division as you would with two positive numbers.
-
Add the negative sign: Attach a negative sign to the result obtained in step 3.
Example 1:
Solve: 24 ÷ (-6)
- Dividend: 24; Divisor: -6
- Rule: Positive divided by negative is negative.
- Division: 24 ÷ 6 = 4
- Negative sign: -4
Therefore, 24 ÷ (-6) = -4
Example 2:
Solve: 15 ÷ (-3)
- Dividend: 15; Divisor: -3
- Rule: Positive divided by negative is negative.
- Division: 15 ÷ 3 = 5
- Negative sign: -5
Therefore, 15 ÷ (-3) = -5
Example 3 (with decimals):
Solve: 10.5 ÷ (-2.1)
- Dividend: 10.5; Divisor: -2.1
- Rule: Positive divided by negative is negative.
- Division: 10.5 ÷ 2.1 = 5
- Negative sign: -5
Therefore, 10.5 ÷ (-2.1) = -5
Example 4 (with fractions):
Solve: (1/2) ÷ (-1/4)
- Dividend: 1/2; Divisor: -1/4
- Rule: Positive divided by negative is negative.
- Division: (1/2) ÷ (1/4) = (1/2) * (4/1) = 2
- Negative sign: -2
Therefore, (1/2) ÷ (-1/4) = -2
Real-World Applications
Understanding the division of positive numbers by negative numbers is crucial in various real-world scenarios:
-
Finance: Calculating losses or debts. For instance, if a company loses $10,000 over 5 months, the average monthly loss is calculated as $10,000 ÷ (-5 months) = -$2000 per month.
-
Temperature: Determining the average rate of temperature decrease. If the temperature drops 15 degrees over 3 hours, the average decrease is 15 ÷ (-3) = -5 degrees per hour.
-
Physics: Calculating acceleration or deceleration. A negative value indicates deceleration.
-
Engineering: Analyzing changes in pressure or velocity, where negative values represent decreases.
Common Mistakes and How to Avoid Them
Many students struggle with this concept initially due to a few common mistakes:
-
Ignoring the signs: This leads to incorrect results. Always remember to account for the sign of both the dividend and the divisor.
-
Incorrectly applying the rule: Ensure you understand that a positive divided by a negative always results in a negative.
-
Confusing with other operations: Don't confuse division with subtraction or multiplication.
To avoid these errors, take your time, break down the problem into steps, and double-check your work. Practice regularly with various examples to solidify your understanding.
Frequently Asked Questions (FAQs)
Q1: What happens if I divide a negative number by a positive number?
A1: When a negative number is divided by a positive number, the result is always negative. This is the opposite scenario, but the sign rule remains consistent.
Q2: What if both numbers are negative?
A2: If both the dividend and the divisor are negative, the result is positive. A negative divided by a negative cancels out the negative signs.
Q3: Can I divide by zero?
A3: No, division by zero is undefined in mathematics. It's a fundamental concept that leads to inconsistencies and paradoxes.
Q4: How can I improve my understanding of this concept?
A4: Practice is key! Work through numerous examples, starting with simple problems and gradually increasing the complexity. Use different types of numbers (whole numbers, decimals, fractions) to broaden your experience. Consider using online resources, such as interactive math websites or educational videos, to reinforce your learning.
Conclusion: Mastering the Concept
Understanding the division of positive numbers by negative numbers is a foundational skill in mathematics. By grasping the core rule, practicing regularly, and addressing common misconceptions, you can build a solid understanding of this concept and apply it confidently in various mathematical and real-world contexts. Remember, consistent practice and a clear understanding of the underlying principles are crucial to mastering this aspect of arithmetic. Don't hesitate to review this material and seek additional practice opportunities as needed. With patience and persistence, you'll confidently navigate these calculations.
Latest Posts
Latest Posts
-
How To Take Ln Of Both Sides
Sep 20, 2025
-
Which Substance Can Be Broken Down By A Chemical Change
Sep 20, 2025
-
Does H2o Have Dipole Dipole Forces
Sep 20, 2025
-
1 10 000 As A Power Of 10
Sep 20, 2025
-
For The Chemical Equation So2 No2
Sep 20, 2025
Related Post
Thank you for visiting our website which covers about Positive Number Divided By A Negative Number . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.