Is The Square Root Of 1 1
faraar
Sep 07, 2025 · 5 min read
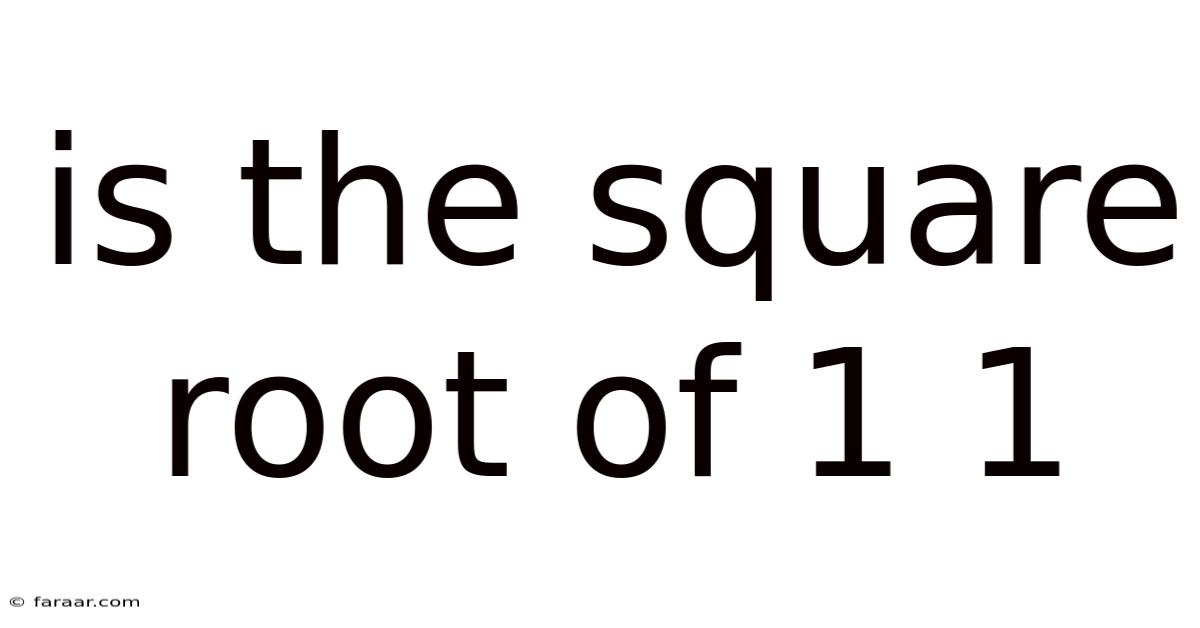
Table of Contents
Is the Square Root of 1, 1? A Deep Dive into Radicals and Their Properties
The question, "Is the square root of 1, 1?" seems deceptively simple. A quick glance might lead to an immediate "yes," and for many practical applications, that's a perfectly acceptable answer. However, delving deeper reveals a fascinating exploration of mathematical concepts, including radicals, their properties, and the nuances of mathematical notation. This article will not only answer the question definitively but will also illuminate the underlying principles and explore related mathematical ideas.
Understanding Square Roots and Radicals
Before we definitively answer the central question, let's establish a firm understanding of what a square root is. A square root is a number that, when multiplied by itself, produces a given number. In other words, if x² = y, then x is the square root of y. The symbol used to denote the square root is √, also known as a radical. The number under the radical sign (√) is called the radicand.
For example:
- √9 = 3 because 3 x 3 = 9
- √16 = 4 because 4 x 4 = 16
- √25 = 5 because 5 x 5 = 25
The concept extends beyond positive integers. We can also find the square roots of negative numbers (resulting in imaginary numbers, denoted by i, where i² = -1) and fractions.
The Principal Square Root
This is where things get slightly more complex. Consider the equation x² = 9. This equation has two solutions: x = 3 and x = -3, since both 3 x 3 = 9 and (-3) x (-3) = 9. This means that 9 has two square roots: 3 and -3.
However, when we use the radical symbol √, we are typically referring to the principal square root. The principal square root is the non-negative square root. Therefore:
- √9 = 3 (the principal square root)
While -3 is also a square root of 9, it is not the principal square root. This distinction is crucial for maintaining consistency and avoiding ambiguity in mathematical calculations.
Answering the Question: Is √1 = 1?
Now, we can definitively address the central question: Is the square root of 1, 1? The answer is yes.
Let's analyze this using the definition of a square root and the concept of the principal square root:
- 1 x 1 = 1
Therefore, 1 is a square root of 1. Furthermore, since 1 is a non-negative number, it is also the principal square root of 1. Hence, √1 = 1.
Exploring Beyond the Basics: Higher-Order Roots and Complex Numbers
While the square root of 1 is straightforward, the concept of roots extends beyond just the square root. We can have cube roots (∛), fourth roots (∜), and so on. These are called higher-order roots.
- The nth root of a number x is a number y such that yⁿ = x.
For example:
- ∛8 = 2 (because 2 x 2 x 2 = 8)
- ∜16 = 2 (because 2 x 2 x 2 x 2 = 16)
The concept of roots also extends into the realm of complex numbers. Recall that imaginary numbers involve the imaginary unit i, where i² = -1. Complex numbers are numbers that have both a real and an imaginary part, written in the form a + bi, where a and b are real numbers.
For instance, finding the square roots of -1 leads us into the realm of complex numbers:
√(-1) = ±i
Illustrative Examples and Applications
Let's solidify our understanding with some examples showcasing how the square root of 1 is utilized in different contexts:
1. Geometry: The concept of square roots is fundamental in geometry, particularly when dealing with distance calculations using the Pythagorean theorem (a² + b² = c²). If we consider a right-angled triangle with sides a = 0 and b = 1, then c² = 0² + 1² = 1, leading to c = √1 = 1. This is the simplest possible application of the Pythagorean theorem.
2. Algebra: Square roots often appear in solving quadratic equations. For example, the equation x² - 1 = 0 can be solved by factoring or using the quadratic formula, leading to solutions x = ±√1 = ±1.
3. Calculus: In calculus, the derivative of a function might involve calculating the square root of an expression. If the expression evaluates to 1, then the square root will be 1, simplifying subsequent calculations.
4. Computer Science: In computer algorithms and data structures, square roots are crucial in various applications, such as calculating distances in coordinate systems or determining the efficiency of certain algorithms. When dealing with simplified cases, the square root of 1 directly contributes to the simplicity of the calculations.
Frequently Asked Questions (FAQ)
Q1: Are there any other numbers whose square root is itself?
A1: Yes, besides 1, the number 0 also has this property: √0 = 0. These are the only non-negative real numbers with this characteristic.
Q2: Can the square root of a number ever be negative?
A2: The principal square root is always non-negative. However, a number can have a negative square root, as illustrated by the example of √9 = ±3. The negative square root is denoted by -√9 = -3.
Q3: How is the square root of 1 used in real-world applications?
A3: While seemingly trivial, the square root of 1 is fundamental in simplifying calculations across various fields. Its simplicity helps in reducing computational complexity in numerous applications, often serving as a base case or a simple example. It's the foundation upon which more complex mathematical operations are built.
Q4: What about the square roots of other numbers close to 1?
A4: Understanding the behavior of square roots near 1 is essential. The square root function is continuous, so as numbers approach 1, their square roots also approach 1. For example, √0.9 ≈ 0.9487 and √1.1 ≈ 1.0488.
Conclusion
The seemingly simple question, "Is the square root of 1, 1?" opens a door to a deeper understanding of fundamental mathematical concepts. While the answer is a straightforward "yes," the exploration reveals the importance of distinguishing between the principal square root and other roots, the extension to higher-order roots and complex numbers, and the ubiquitous presence of square roots in various mathematical and scientific disciplines. Understanding these concepts helps build a strong foundation for further mathematical learning and applications. The apparent simplicity of √1 = 1 underscores the power of foundational mathematical principles in solving more complex problems. This seemingly simple equation forms a cornerstone for numerous advanced mathematical concepts and calculations.
Latest Posts
Latest Posts
-
Can Homophones Be Spelled The Same
Sep 07, 2025
-
How To Find Angles Of Parallelogram
Sep 07, 2025
-
Why Does My Room Smell Like Popcorn
Sep 07, 2025
-
What Is The Value Of X 70 35
Sep 07, 2025
-
1 3 1 12 As A Fraction
Sep 07, 2025
Related Post
Thank you for visiting our website which covers about Is The Square Root Of 1 1 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.